Estudios de asociación cruzada.

Los estudios de asociación cruzada son estudios transversales que estudian más de una variable para determinar si existe asociación entre ellas.
Espero, por vuestro bien, que nunca os hayáis tenido que ver en la situación de pronunciar esta frase. Y espero, también por vuestro bien, que si habéis tenido que pronunciarla en alguna ocasión no se viese precedida por la palabra “cariño”. ¿O sí?. Dejémoslo a la conciencia de cada cual.
Lo que sí es cierto es que esta frase debemos planteárnosla en forma de pregunta en una situación mucho menos escabrosa: al contemplar los resultados de un estudio transversal. Obvia decir, claro está, que, en estos casos, el cariño no es imprescindible.
Estudios de asociación cruzada
Los estudios descriptivos transversales son un tipo de estudio observacional en los que se extrae una muestra representativa de la población que queremos estudiar y se mide la frecuencia de la enfermedad o el efecto que nos interese en los individuos de la muestra. Cuando medimos más de una variable, estos estudios se denominan de asociación cruzada, ya que nos permiten averiguar si las variables medidas guardan algún tipo de asociación.
Pero estos estudios tienen dos características que debemos tener siempre en cuenta. Primero, son estudios de prevalencia que miden la frecuencia en un momento concreto, por lo que el resultado puede variar en función del momento elegido para medir la variable. Segundo, como la medición se realiza de forma simultánea, resulta difícil establecer una relación causa-efecto, algo que a todos nos encanta hacer. Pero es algo que debemos evitar hacer porque, con este tipo de estudios, las cosas no son siempre lo que parecen. O, mejor dicho, las cosas pueden ser bastantes más cosas de lo que parecen.
¿De qué hablamos?. Veamos un ejemplo. Estoy un poco aburrido de ir al gimnasio, porque me canso cada vez más y mi estado físico… bueno, dejémoslo simplemente en que me canso, así que quiero estudiar si realmente el esfuerzo puede recompensarme con un mejor control de mi 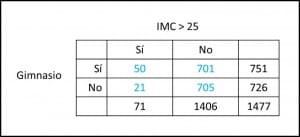
Si os fijáis en los resultados de la tabla podéis comprobar que la prevalencia de sobrepeso-obesidad entre los que van al gimnasio (50/751, alrededor de un 7%) es mayor que entre los que no van (21/726, alrededor del 3%). ¡Horror!, pienso, no solo me canso, sino que los que van al gimnasio tienen el doble de probabilidades de ser obesos. Conclusión: mañana mismo me borro.
¿Veis lo fácil que es llegar a una conclusión absurda (más bien estúpida, en este caso)?. Pero los datos están ahí, así que habrá que buscar una explicación para entender por qué nos indican algo que va en contra de nuestro sentido común. Y hay varias explicaciones posibles para interpretar estos resultados.
La primera, que realmente ir al gimnasio favorezca que uno engorde. Parece poco probable, pero nunca se sabe… Imaginemos que el entrenamiento motiva que los deportistas coman como fieras durante las seis horas siguientes a la sesión deportiva.
La segunda, que los obesos que van al gimnasio vivan más años que los que no. Pensemos que el ejercicio prevenga la muerte por enfermedad cardiovascular en pacientes obesos. Explicaría por qué hay más obesos (en proporción) en el gimnasio que fuera de él: simplemente se morirían menos que los que no van. Al fin y al cabo estamos tratando con un estudio de prevalencia, por lo que vemos el resultado final en el momento de la medición.
Causalidad inversa
La tercera posibilidad es que la enfermedad pueda influir en la frecuencia de la exposición, lo que se conoce como causalidad inversa. En nuestro ejemplo, podría haber más obesos en el gimnasio porque una de las recomendaciones de tratamiento que se les diese a los obesos fuese esa: apuntarse a un gimnasio. Esta ya no suena tan ridícula como la primera.
Pero todavía hay más posibles explicaciones. Hasta ahora hemos tratado de explicar una asociación entre las dos variables que hemos asumido como real. Pero, ¿y si la asociación no es real?. ¿Cómo podemos obtener una asociación falsa entre las dos variables?. De nuevo, tenemos tres explicaciones posibles.
La primera, nuestro viejo conocido: el azar. Algunos me diréis que podemos calcular la significación estadística o los intervalos de confianza pero, ¿y qué?. Aún en el caso de significación estadística, lo que quiere decir es que no podemos descartar que haya sido el azar con un cierto grado de incertidumbre. Incluso con p<0,05, siempre habrá una probabilidad de que cometamos un error de tipo I y descartemos erróneamente el efecto del azar. Podemos medir el azar, pero nunca librarnos de él.
Sesgo de selección
La segunda es que hayamos cometido algún tipo de sesgo que invalide nuestros resultados. A veces, las características de la enfermedad pueden hacer que la probabilidad de elegir a sujetos expuestos y no expuestos no sea la misma, produciéndose un sesgo de selección. Imaginemos que en lugar de una encuesta (telefónica, por ejemplo) hemos usado un registro médico.
Puede ocurrir que los obesos que van al gimnasio sean más responsables con el cuidado de su salud y vayan más al médico que los otros, con lo que será más probable que incluyamos obesos deportistas en el estudio, haciendo una estimación al alza de la proporción real.
Otras veces el factor de estudio puede ser algo mal visto o estigmatizante desde el punto de vista social, así que los que lo padezcan no tendrán las mismas ganas de participar en el estudio (y reconocer el padecimiento) que los que no, así que su frecuencia se subestimará.
Sesgo de clasificación
En nuestro ejemplo, podría ocurrir que los obesos que no van al gimnasio respondiesen a la encuesta mintiendo sobre su peso verdadero, con lo cual se clasificarían erróneamente. Este sesgo de clasificación puede ocurrir aleatoriamente en los dos grupos de expuestos y no expuestos, con lo que cual tiende a favorecer la falta de asociación (la hipótesis nula), de tal forma que se subestima la asociación, si es que ésta existe.
El problema es cuando este error es sistemático en uno de los dos grupos, ya que esto puede tanto subestimar como infraestimar la asociación entre exposición y enfermedad.
Variable de confusión
Y, por fin, la tercera posibilidad es que exista una variable confusora que se distribuya de manera diferente entre expuestos y no expuestos. Se me ocurre pensar que los que van al gimnasio son más jóvenes que los que no. Es posible que los obesos más jóvenes tengan más tendencia a ir al gimnasio. Si estratificamos los resultados por la variable confusora, la edad, podemos determinar su influencia en la asociación.
Para terminar, solo me queda pedir disculpas a todos los obesos del mundo por utilizarlos como ejemplo pero es que, por una vez, quería dejar tranquilos a los fumadores.
Nos vamos…
Como veis, las cosas no son siempre lo que parecen a primera vista, por lo que hay que interpretar los resultados con sentido común y a la luz de los conocimientos existentes, evitando caer en la trampa de establecer relaciones causales a partir de asociaciones detectadas mediante estudios observacionales. Para establecer relaciones de causa y efecto son siempre necesarios estudios experimentales, el paradigma de los cuales es el ensayo clínico. Pero esa es otra historia…

Muy buenos ejemplos gracias!! me ayudo mucho la apreciacion. En este caso, de que manera se puede disminuir la ocurrencia de la causalidad inversa? eligiendo otro tipo de diseño que no sea transversal?? gracias
Gracias por tu comentario, Gabriela.
Efectivamente, la causalidad inversa tiene su origen el el error de asumir una relación de causalidad entre dos hechos que están correlacionados.
La única forma que puede demostrar la relación de causa-efecto es realizar estudios experimentales (ensayos clínicos aleatorizados), donde se equilibren lo mejor posible las variables confusoras que puedan existir.