Confusión en casos y controles.

Hay que controlar los factores de confusión en casos y controles: una de las técnicas es el emparejamiento.
Vimos en la entrada anterior cómo los estudios observacionales, más concretamente los estudios de cohortes y los de casos y controles, están llenos de trampas y vericuetos. Una de estas trampas es la puerta de atrás por la que se nos escapan los datos, de forma que obtenemos medidas de estimación de asociación erróneas. Esta puerta trasera son los llamados factores de confusión.
Ya sabemos que hay varias formas de controlar la confusión. Una de ellas, el emparejamiento, tiene sus peculiaridades según la empleemos con estudios de cohortes o con estudios de casos y controles.
Confusión en casos y controles
Cuando se trata de estudios de cohortes, el emparejar por el factor de confusión nos permite obtener una medida de asociación ajustada. Esto es así porque controlamos la influencia de la variable confusora sobre la exposición y sobre el efecto. Sin embargo, lo anterior no se cumple cuando utilizamos la técnica de emparejamiento en un estudio de casos y controles.
El diseño de este tipo de estudios nos impone la obligación de realizar el emparejamiento una vez que se ha producido el efecto. De esta forma, los pacientes que actúan como controles no constituyen un conjunto de individuos independientes elegidos al azar, ya que cada control fue seleccionado cumpliendo una serie de criterios determinados según el caso con el que se emparejó.
Esto, lógicamente, evita que podamos seleccionar otros individuos de la población que no cumplen los criterios especificados pero que serían potencialmente incluibles en el estudio. Si nos olvidamos de este pequeño detalle y aplicamos la misma metodología de análisis que usaríamos en un estudio de cohortes incurriríamos en un sesgo de selección que invalidaría nuestros resultados. Además, aunque conseguimos forzar una distribución similar del factor de confusión, solo controlamos totalmente su influencia sobre el efecto, pero no sobre la exposición.
Así que la mentalidad del análisis varía un poco cuando valoramos los resultados de un estudio de casos y controles en los que hemos utilizado la técnica de emparejamiento para controlar factores de confusión. Mientras que en un estudio sin emparejamiento analizamos la asociación entre exposición y efecto en el grupo global, cuando hemos emparejado debemos estudiar el efecto en las parejas de caso-control.
Emparejamiento y ajuste
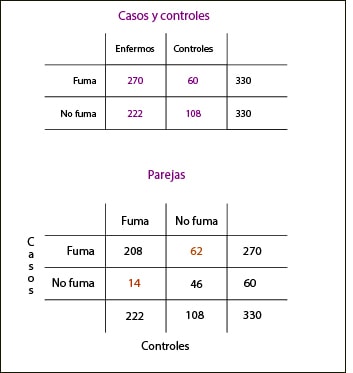
En la tabla superior vemos los datos globales del estudio. Si analizamos los datos sin tener en cuenta que hemos utilizado el emparejamiento para seleccionar los controles obtenemos una odds ratio de 2,18, como vimos en la entrada anterior. Sin embargo, sabemos que esta estimación es errónea. ¿Qué hacemos?. Considerar el efecto de las parejas, pero solo de las mal avenidas.
Vemos en la tabla inferior la distribución de las parejas en función de su exposición al tabaco. Tenemos 208 parejas en las que tanto el caso (persona con cáncer laríngeo) como el control son fumadores. Al estar los dos sometidos a la exposición no nos servirán para estimar su asociación con el efecto. Lo mismo puede decirse de las 46 parejas en las que ni el caso ni el control fuman. Las parejas que nos interesan son las 14 en las que el control fuma pero el caso no lo hace y las 62 en las que solo fuma el caso, pero no el control.
Estas parejas discordantes son las únicas que nos dan información sobre el efecto del tabaco sobre la aparición del cáncer de laringe. Si calculamos la odds ratio vemos que es de 62/14 = 4,4, una medida de asociación más fuerte que la que obtuvimos previamente y, sin duda, mucho más próxima a la realidad.
Nos vamos…
Por último, solo me resta hacer tres consideraciones antes de terminar. La primera es, aunque no creo que haga falta, recordaros que los datos son producto de mi imaginación y que el ejemplo es totalmente ficticio aunque no parezca tan estúpido como otros que inventé en otras entradas. La segunda, que estos cálculos suelen hacerse con programas informáticos o calculadoras, utilizando la prueba de Mantel-Haenszel o la prueba de McNemar.
La tercera, comentar que en todos estos ejemplos hemos utilizado un emparejamiento con una relación 1:1 (un control por cada caso), pero esto no tiene por qué ser obligatoriamente así ya que, en algunas ocasiones, puede interesar utilizar más de un control por cada caso. Esto conlleva sus diferencias sobre la influencia del factor de confusión sobre la medida de asociación estimada y sus consideraciones a la hora de realizar el análisis. Pero esa es otra historia…
