Inconvenientes del cribado.

Antes de poner en marcha un programa de cribado, debemos plantear bien la estrategia e identificar sus ventajas e inconvenientes.
Cualquier persona sensata como es debido nos dirá que siempre es mejor prevenir que curar. Yo lo he oído millones de veces. Incluso había un programa de televisión que se llamaba “Más vale prevenir”. Además, nadie en su sano juicio duda de los beneficios en salud que la Medicina Preventiva ha conseguido promoviendo la mejora de los estilos de vida, controlando las condiciones del ambiente o con los programas de vacunaciones. Pero, sin embargo, cuando hablamos de programas de cribado (los angloparlantes utilizan una palabra horrorosa: screening), yo os diría que no siempre está tan claro que sea mejor prevenir y que, en algunas ocasiones, es mejor no hacer nada por dos motivos. El primero, porque nuestros recursos son limitados y todo lo que gastemos en cribar saldrá de algún otro sitio que pasará a tener menos recursos. El segundo, porque aunque nos mueva la mejor de las voluntades, si intentamos prevenir de forma indiscriminada podemos producir más daño que beneficio.
Estrategia del cribado
Habrá, pues, que pensar si está justificada cualquier estrategia de cribado antes de ponerla en práctica. La prueba diagnóstica con la que pensemos hacer el cribado tiene que ser sencilla, barata, fiable y con buena aceptabilidad por parte de la población. Es importante no olvidar que a los que vamos a hacer la prueba son individuos sanos a los que puede no apetecerles mucho que les vayamos incordiando. Además, es raro que para confirmar el diagnóstico baste con un solo resultado positivo, y las pruebas de confirmación seguro que son más caras y molestas, cuando no claramente invasoras (pensemos un cribado que haya que confirmar con una biopsia). Habrá que considerar la sensibilidad y especificidad de la prueba ya que, aunque a una prueba de cribado le perdonemos un cierto número de falsos positivos, si el diagnóstico de confirmación es muy caro o muy molesto, mejor que los falsos positivos sean pocos, o el cribado no nos saldrá rentable.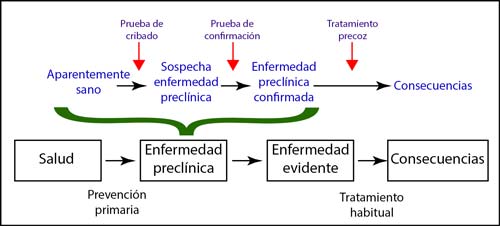
Por otra parte, para que merezca la pena hacer un cribado, la enfermedad que queramos prevenir tiene que tener una fase preclínica larga. Si esto no es así, tendremos pocas oportunidades para detectarla. El problema es, claro está, que las que más nos interesa detectar son las enfermedades más graves, y estas suelen tener las fases preclínicas sin síntomas más cortas.
Además, ¿a quién le hacemos el cribado?. A todo el mundo, me diréis. El problema es que esto es lo más caro, sobre todo teniendo en cuenta que los sanos no suelen ir al médico y vamos a tener que buscarles de forma activa si queremos cribarles (por su bien, eso sí). A los que están enfermos, pero poco todavía, me diréis entonces. Pues poco beneficio, ya que estos, cuando van al médico, están ya fuera del alcance de la prevención (ya están enfermos). Bueno, pues aprovechemos los que van al médico por otros motivos, propondréis alguno. Pues esto, que se llama cribado de oportunidad, es lo que se hace en muchas ocasiones por una cuestión práctica. Sale más barato, pero se pierden los beneficios teóricos del cribado universal. El hacer cribado a un número lo mayor posible tiene especial interés cuando lo que se detectan son factores de riesgo (por ejemplo, hipertensión), ya que, además de las ventajas del tratamiento precoz, tendremos oportunidad de hacer prevención primaria, mucho más económica y con mejores resultados en salud.
Así que, como vemos, hacer cribado puede tener múltiples ventajas que a todo el mundo le resultan evidentes. El problema es que rara vez nos paramos a pensar en el daño que podemos hacer con esta forma de prevención. ¿Cómo es posible que una detección temprana de una enfermedad o la oportunidad de hacer un tratamiento precoz puedan perjudicar a alguien?. Hagamos algunas reflexiones.
Inconvenientes del cribado
La prueba puede doler (un pinchazo) o ser engorrosa (meter las heces de tres días en un bote). Pero si esto os parece una chorrada, pensad en el que tiene un infarto realizando una prueba de esfuerzo, el que tiene un choque anafiláctico por un contraste o el japonés que se gana una perforación durante una colonoscopia. Eso ya es harina de otro costal. Además, la simple perspectiva del cribado puede generar ansiedad o estrés en una persona sana que no debería estar preocupada por ello.
Y que me decís si la prueba es positiva. Imaginaos que, para confirmar el diagnóstico hay que endoscopiar o hacer una biopsia corial, por no hablar de la ansiedad hasta que se descarte el diagnóstico con la prueba de confirmación. Y, aunque se confirme, el beneficio puede ser escaso: ¿qué beneficio tiene para el bienestar de una persona asintomática decirle que tiene una enfermedad, cuando igual no tiene tratamiento o no hay que comenzarlo todavía?. Pero es que, aunque haya tratamiento, éste también puede dañar. Como ejemplo muy al día están los efectos de una prostatectomía profiláctica por un carcinoma de bajo grado detectado con el cribado del PSA: se le puede dejar incontinente o impotente (o las dos cosas) por hacer una intervención que probablemente podría haberse retrasado años.
Pensad siempre que los beneficios potenciales de un cribado en población general sana pueden ser escasos precisamente por eso, porque se trata de personas sanas. Si existe el más mínimo daño que se pueda derivar de las estrategia de cribado o del tratamiento precoz deberemos considerar seriamente si merece la pena realizar el programa de cribado.
Razones para hacer un cribado
Entonces, ¿cuándo hacemos el cribado de una determinada enfermedad?. Lo primero, cuando la carga de enfermedad que produce la patología nos haga pensar que merece la pena. La carga de enfermedad depende de la prevalencia y de la gravedad. Si una enfermedad es muy frecuente pero muy benigna la carga de enfermedad será baja y probablemente no interese cribar. En el caso de que sea muy rara tampoco suele ser rentable cribar, excepto si la enfermedad es muy grave y tiene un tratamiento muy eficaz que previene sus complicaciones. Un ejemplo sería el cribado de hiperfenilalaninemia en recién nacidos.
Lo segundo, tenemos que disponer de una pruebaadecuada con las características que hemos comentado, sobre todo que el número de falsos positivos no sea demasiado alto para no tener que andar confirmando el diagnóstico en demasiados sanos y hacer un negocio ruinoso.
Lo tercero, tiene que haber un tratamiento precoz que, además, tiene que ser más eficaz que el habitual al comenzar los síntomas. Además, tenemos que disponer de los recursos para realizar ese tratamiento.
Cuarto, tanto la prueba de cribado como el tratamiento que se derive del resultado positivo tienen que ser seguros. De lo contrario, podríamos hacer más daño que el que queremos evitar.
Y, quinto, debemos hacer un balance entre los costes y los potenciales beneficios del cribado. No hay que olvidar que, aunque la prueba no sea muy cara, se la vamos a hacer a un montón de gente, por lo que tendremos que gastarnos un montón de dinero, recurso más bien escaso en los tiempos que corren.
Nos vamos…
Para terminar, deciros que todo programa de cribado debe completarse con los estudios que comprueben su efectividad. Esto puede hacerse por métodos directos o indirectos según se compare la posibilidad de cribar o no cribar o se estudien las diferentes intervenciones de la estrategia de cribado por separado. Pero esa es otra historia…
