Ensayo clínico cruzado.

El ensayo clínico cruzado permite que cada paciente reciba la intervención en estudio y la de control, en un orden determinado.
Dicen los matemáticos que dos líneas paralelas son aquellas que, por más que se prolongan, nunca se juntan. ¿Nunca? A mí me parece que nunca es mucha distancia. No creo que nadie haya prolongado dos paralelas lo suficiente como para estar seguro de esta afirmación. Claro que, por otro lado, si llegan a juntarse es que no eran paralelas, ¿verdad?
Las que sí pueden juntarse, e incluso cruzarse, son las dos ramas de un ensayo en paralelo, dando lugar a un nuevo diseño que llamamos ensayo clínico cruzado.
Ensayo clínico cruzado
En un ensayo clínico en paralelo clásico cada participante se asigna aleatoriamente a una, y solo una, de las ramas del ensayo, la de intervención en estudio o la de control. Sin embargo, podemos cruzar las paralelas y conseguir un diseño que permite que cada paciente reciba tanto la intervención en estudio como la de control siempre, eso sí, estableciendo un orden determinado y durante un periodo de tiempo establecido. 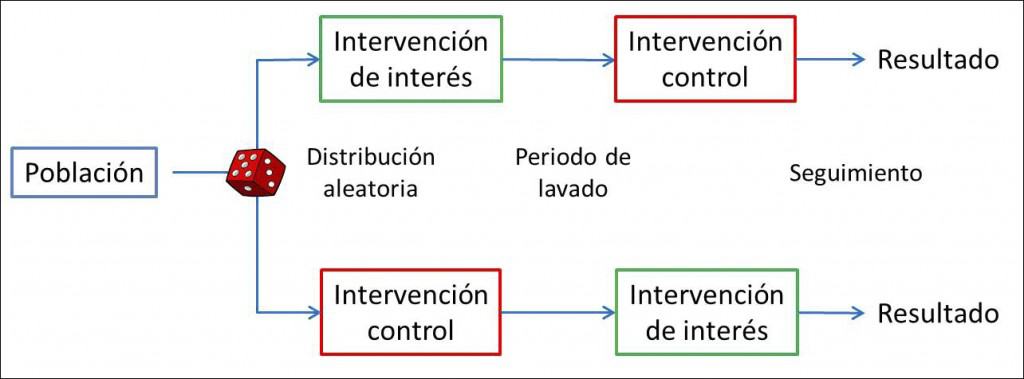
Existen algunas variaciones sobre el tema de los ensayos cruzados, según todos los participantes sean sometidos a las dos intervenciones (ensayo completo) o algunos solo a una de ellas (ensayo incompleto). Además, es posible extender este tipo de diseño y probar más de dos intervenciones, dando lugar a distintos órdenes de secuencia que reciben nombres como diseño doble, de Balaam, cuadrado latino, etc, en los que no vamos a profundizar en esta entrada.
Sus ventajas
La ventaja principal de los estudios cruzados radica en una característica que ya hemos comentado: cada sujeto actúa como su propio control. Esto, que puede parecer una chorrada sin importancia, no es tal. Si lo pensamos un poco, lo que hacemos es valorar el efecto de la intervención activa y de la de control en el mismo sujeto, con lo cual obtendremos menor variabilidad que si comparamos los efectos en participantes diferentes, como se hace en el ensayo en paralelo, en el que cada participante se expone solo a una de las dos intervenciones.
Al ser menor la variabilidad, la precisión de las observaciones será mayor, con lo que el tamaño muestral necesario para detectar una determinada diferencia de efecto del tratamiento será menor. Y no un poco menor, sino que la muestra necesaria puede verse reducida de forma importante en comparación con la que haría falta en el ensayo paralelo correspondiente.
Esta reducción del tamaño de la muestra depende de la correlación entre las distintas medidas de resultado del estudio. En el peor de los casos, con una correlación cero, la muestra se ve dividida por la mitad. Si la correlación es de 0,5, la muestra necesaria será de la cuarta parte. Pero es que esta reducción es cada vez mayor según el valor de la correlación se vaya aproximando a uno.
Por si fuera poco, además de una estimación más precisa, ésta es menos sesgada, ya que se asume una respuesta constante de cada sujeto a las dos intervenciones probadas, mientras que en el ensayo en paralelo esta respuesta es más variable por medirse en sujetos diferentes.
Y sus inconvenientes
Pero no todo va a ser ventajas a favor de los diseños cruzados. También plantean algunos inconvenientes. La mayor limitación es el coñazo que se les da a los participantes con tanta intervención y tanto periodo. Y esto es importante no solo por la consideración que podamos sentir hacia los participantes, sino porque aumenta el riesgo de pérdidas durante el estudio. Y resulta que los estudios cruzados son más sensibles a las pérdidas durante el seguimiento que los paralelos, sobre todo si el número de participantes que completan cada secuencia es diferente.
Otra limitación es que es importante que los sujetos sean similares al comienzo de cada periodo, por lo que estos estudios solo sirven si se trata de enfermos crónicos con síntomas estables. Tampoco sirven si la variable de resultado produce un efecto permanente. Pensemos en la más permanente de todas, la mortalidad. Si el participante se muere en el primer periodo, será más que difícil valorar su respuesta en el periodo siguiente.
Además, alguna de sus ventajas, como el reducido tamaño muestral, se torna en inconveniente en algunas ocasiones. Esto ocurre, por ejemplo, en estudios de fase III, en los que queramos valorar seguridad, tolerancia, eficacia, detección de efectos adversos impredecibles, etc. En estos casos, la muestra pequeña no solo no es imprescindible, sino que puede resultar inadecuada.
Tres aspectos característicos
Por último, referirnos a tres debilidades desde el punto de vista de diseño, los llamados efecto residual, efecto secuencia y efecto periodo.
El efecto residual se produce cuando en un periodo persiste el efecto de la intervención del periodo anterior. Pensemos que hemos dado un fármaco y quedan aún restos en sangre. Evidentemente, esto se soluciona prolongando el periodo de lavado, pero hay ocasiones en que esto no es tan fácil. Pensemos en un tratamiento hipotensor en el que la respuesta en el segundo periodo sea más favorable por el simple hecho de estar incluido en el estudio (efecto placebo).
El efecto secuencia se produce cuando el orden de las intervenciones afecta el resultado final, con lo que solo podríamos valorar adecuadamente los resultados de la primera intervención.
Por último, puede ocurrir que las características del paciente cambien a lo largo del estudio, modificando su respuesta a las diferentes intervenciones. Nos encontramos ante un efecto periodo.
Los ensayo clínicos cruzados son, en resumen, más eficientes en cuanto a tamaño muestral que los ensayos paralelos, siempre que se cumplan las condiciones óptimas para su empleo. Son muy útiles para estudios de fase I y fase II en los que queremos conocer la farmacocinética y farmacodinámica, la seguridad, la titulación de dosis, etc. En fases posteriores del desarrollo de nuevos fármacos son menos útiles, sobre todo si, como ya hemos comentado, no se trata de enfermedades crónicas con sintomatología estable.
Nos vamos…
Y aquí dejamos los ensayos cruzados. No hemos hablado nada del análisis estadístico de los resultados. En el caso del ensayo en paralelo los resultados de las dos ramas pueden compararse directamente, pero esto no es así con los ensayos cruzados, en los que deberemos asegurarnos de que no se haya producido efectos residual, efecto secuencia o efecto periodo. Pero esa es otra historia…
