Odds ratio diagnóstica.

La odds ratio diagnóstica es un marcador de prueba diagnóstica fácil de interpretar y que no depende de la prevalencia de la enfermedad.
Hoy no vamos a hablar de dragones que te llevan de paseo si te pones en su chepa. Tampoco vamos a hablar de hombres con los pies en la cabeza ni de ninguna otra de las criaturas de la mente delirante de Michael Ende. Hoy vamos a hablar de otra historia que no tiene fin: el de los indicadores de pruebas diagnósticas.
Valoración de pruebas diagnósticas
Cuando uno cree que los conoce todos, levanta una piedra y encuentra otro más debajo de ella. ¿Y por qué hay tantos?, os preguntaréis. Pues la respuesta es muy sencilla. Aunque hay indicadores que nos interpretan muy bien cómo trata la prueba diagnóstica a los sanos y a los enfermos, todavía se busca un buen indicador, único, que nos dé una idea de la capacidad diagnóstica del test.
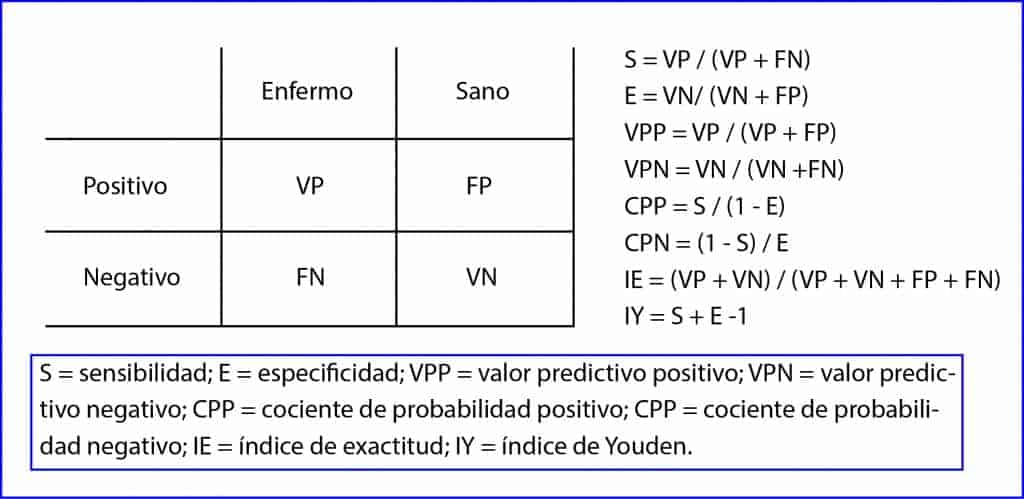
El problema es que la mayoría de ellos valoran parcialmente la capacidad de la prueba, por lo que necesitamos utilizarlos en parejas: sensibilidad y especificidad, por ejemplo. Solo los dos últimos que hemos enunciado funcionan como indicadores únicos. El índice de exactitud mide el porcentaje de pacientes correctamente diagnosticados, pero trata por igual a positivos y negativos, verdaderos o falsos. Por su parte, el índice de Youden suma los mal clasificados por la prueba diagnóstica.
En cualquier caso, no se recomienda utilizar ni el índice de exactitud ni el de Youden de forma aislada si queremos valorar una prueba diagnóstica. Además, este último es un término difícil de trasladar a un concepto clínico tangible al ser una transformación lineal de la sensibilidad y la especificidad.
Llegados a este punto se entiende lo que nos gustaría disponer de un indicador único, sencillo, cuya interpretación nos resultase familiar y que no dependiese de la prevalencia de la enfermedad. Sería, sin duda, un buen indicador de la capacidad de la prueba diagnóstica que nos evitaría tener que recurrir a una pareja de indicadores.
Odds ratio diagnóstica
Y aquí es donde a alguna mente brillante se le ocurre utilizar un indicador tan conocido y familiar como la odds ratio para interpretar la capacidad de la prueba. Así, podemos definir la odds ratio diagnóstica (ORD) como la razón de la odds de que el enfermo dé positivo con respecto a la odds de dar positivo estando sano. Como esto parece un trabalenguas, vamos a comentar los dos componentes de la razón.
La odds de que el enfermo dé positivo frente a que dé negativo no es más que la proporción entre verdaderos positivos (VP) y falsos negativos (FN): VP/FN. Por otra parte la odds de que el sano dé positivo frente a que dé negativo es el cociente entre falsos positivos (FP) y verdaderos negativos (VN): FP/VN. Y visto esto, solo nos queda definir la razón entre las dos odds:
La ORD puede también expresarse en función de los valores predictivos y de los cocientes de probabilidad, según las expresiones siguientes:
Como toda odds ratio, los valores posibles de la ORD van de cero a infinito. El valor nulo es el uno, que significa que la prueba no tiene capacidad discriminatoria entre sanos y enfermos. Un valor mayor de uno indica capacidad discriminatoria, que será mayor cuanto mayor sea el valor. Por último, valores entre cero y uno nos indicarán que la prueba no solo no discrimina bien entre enfermos y sanos, sino que los clasifica de forma errónea y nos da más valores negativos entre los enfermos que entre los sanos.
La ORD es un medidor global fácil de interpretar y que no depende de la prevalencia de la enfermedad, aunque hay que decir que sí puede variar entre grupos de enfermos con distinta gravedad de su enfermedad.
Por último, añadir a sus ventajas que existe la posibilidad de construir su intervalo de confianza a partir de la tabla de contingencia usando esta pequeña fórmula que me vais a permitir:
Sí, ya he visto el logaritmo, pero es que las odds son así: al ser asimétricas alrededor del valor nulo estos cálculos hay que hacerlos con logaritmos neperianos. Así, una vez que tenemos el error estándar podemos calcular el intervalo de esta manera:
Solo nos quedaría, finalmente, aplicar los antilogaritmos a los límites del intervalo que obtenemos con la última fórmula (el antilogaritmo es elevar el número e a los límites obtenidos).
Nos vamos…
Y creo que con esto ya está bien por hoy. Podríamos seguir mucho más. La ORD tiene muchas más bondades. Por ejemplo, puede utilizarse con pruebas con resultados cuantitativos (no solo positivo o negativo), ya que existe una correlación entre la ORD y el área bajo la curva ROC de la prueba. Además, puede usarse en metanálisis y en modelos de regresión logística, lo que permite incluir variables para controlar la heterogeneidad de los estudios primarios. Pero esa es otra historia…
