Odds ratio.

The odds ratio allows us to calculate the strength of the association between exposure and effect when we do not know the baseline risks.
Do you like to play? I’m talking about gambling and people going to casinos with the vain hope of winning a little (or no so little) money while having fun. But people who’d like to get rich in a quick and funny way forget two things. First is that everything they can see around them (and much more that they don’t see) has been paid by the thousands who previously failed in a similar attempt at the same place. Second, they forget to previously thoroughly study what are their chances of winning… and their odds.
Odds and probability
You may wonder what an odds is. Well, to answer this question we have to warm up a few neurons.
We all understand the concept of probability. If someone ask what is the probability of getting a six when rolling a die in the casino, we’ll quickly respond that the probability is one in six or one sixth (0.16 or 16.66%). But the gambler may be interested in knowing how much more likely is to get six than not to get it. And the answer to that is not 1/6, but one fifth. Why? Because the probability of getting six is 1/6 and that of getting otherwise is 5/6.
To find out how much more likely is to get six we have to divide 1/6 by 5/6, which will give us one fifth (20%). This is the odds: the probability of an event to occur respect to the probability of not to occur. For those who love formulas, odds = p / (1-p).
Let’s leave the casino for now. I have noticed that those nights that I take a look at the news on the Internet before going to bed I sleep worse. Suppose we take a survey asking people we run into on the street if they sleep well and if the use to watch the news before going to bed and we come up with the results that I show in the table.
Risk ratio and odds ratio
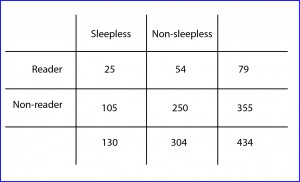
We also calculate the probability that a non-reader being sleepless as the quotient 105/355 = 0.29 (non-sleepless non-readers divided by total non-readers). The odds, meanwhile, would be 105/250 = 0.42 (sleepless non-readers divided by non-sleepless non-readers).
If we now calculate the ratio of the two probabilities we’ll get the risk ratio, RR = 0.31 / 0.29 = 1.06. This means that the risk of having insomnia is more or less the same among those who read the news and those who do not. If we calculate the ratio of the two odds we’ll get a value of 1.09 (0.46/0.42). This is call the odds ratio (OR), an interesting parameter whose utility we’ll soon see.
Let’s now look again to the data in the table, but this time in reverse. What is the probability that an insomniac read the news: 25/130 = 0.19. What are the odds of insomniacs reading respect to non-reading the news: 25/105 = 0.23. What is the probability that you don’t be sleepless but be a reader: 54/304 = 0.17. And the odds: 54/250 = 0.21.
If we calculate the RR = 0.19/0.17 = 1.11, we’ll say that insomniacs have about the same risk of having read the news before going to bed than those who sleep peacefully. What about the odds? The odds is 0.23/0.58 = 1.09. What a surprise! The OR value is the same with independence of the way we manage the data, which must not be a coincidence, but must hide some meaning.
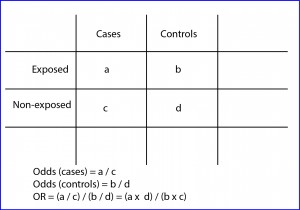
Odds ratio
As with other parameters, the correct way is to calculate confidence intervals to know the accuracy of the estimate. In addition, this association will be statistically significant if the interval does not include the value of one, which is the null value for the OR. The greater the OR the greater is the strength of the association. An OR less than one is more complex to interpret, but we can do a similar reasoning we did when RR was less than one.
But here end the similarities between them. To use RR we need to know the incidence of the effects in the two populations in comparison, while the OR is calculated based on the observed frequency in the two, so they are not comparable parameters although their interpretation is similar. They tend to be equivalent only when the effect has a very low frequency of occurrence. For these reason, the OR is the measure of association used in case-control studies and meta-analysis, whereas RR are preferable for cohort studies and clinical trials.
We’re leaving…
Just a couple of considerations before finishing the issue of OR. First, although it allows us to compare the association between two qualitative variables (categorized as yes or no), it doesn’t serve to establish a cause and effect relationship between them. Second, it’s useful because it allows evaluating the effect of other variables on the association, which has a role in the realization of logistic regression studies. But that’s another story…
