Estudio de la heterogeneidad en el metanálisis.

Métodos numéricos (Q, I, H) y gráficos (Galbraith y L’Abbé) para el estudio de la heterogeneidad de los estudios primarios del metanálisis.
Todos conoceréis el cuento chino del pobre grano de arroz solitario que se cae al suelo y no lo oye nadie. Claro que si en lugar de caerse un grano se cae un saco lleno de arroz eso ya será otra cosa. Hay muchos ejemplos de que la unión hace la fuerza. Una hormiga roja es inofensiva, salvo que te muerda en alguna zona blanda y noble, que suelen ser las más sensibles. Pero ¿qué me decís de una marabunta de millones de hormigas rojas? Eso sí que acojona, porque si se juntan todas y vienen a por ti, poco podrás hacer para parar su empuje. Sí, la unión hace la fuerza.
Y esto también pasa en estadística. Con una muestra relativamente pequeña de votantes bien elegidos podemos estimar quién va a ganar unas elecciones en las que votan millones. Así que, ¿qué no podríamos hacer con un montón de esas muestras? Seguro que la estimación sería más fiable y más generalizable.
Entrando en materia
Pues bien, esta es precisamente una de las finalidades del metanálisis, que utiliza diversas técnicas estadísticas para hacer una síntesis cuantitativa de los resultados de un conjunto de estudios que, aunque tratan de responder a la misma pregunta, no llegan exactamente al mismo resultado. Pero cuidado, no podemos ponernos a juntar estudios para sacar conclusiones sobre la suma de ellos sin antes tomar una serie de precauciones. Esto sería como mezclar churras con merinas que, no sé muy bien porqué, debe ser algo terriblemente peligroso porque todo el mundo sabe que es algo a evitar.
Pensad que tenemos un conjunto de ensayos clínicos sobre un mismo tema y queremos hacer un metanálisis para obtener un resultado global. Es más que conveniente que exista la menor variabilidad posible entre los estudios si queremos combinarlos. Porque, señoras y señores, aquí también impera aquello de juntos, pero no revueltos.
Antes de pensar en combinar los resultados de los estudios de una revisión sistemática para hacer un metanálisis debemos hacer siempre un estudio previo de la heterogeneidad de los estudios primarios, que no es más que la variabilidad que existe entre los estimadores que se han obtenido en cada uno de esos estudios.
Estudio de la heterogeneidad en el metanálisis
En primer lugar, investigaremos posibles causas de heterogeneidad, como pueden ser diferencias en los tratamientos, variabilidad de las poblaciones de los diferentes estudios y diferencias en los diseños de los ensayos. Si existe mucha heterogeneidad desde el punto de vista clínico, quizás lo más idóneo sea no hacer metanálisis y limitarnos a realizar un análisis de síntesis cualitativa de los resultados de la revisión.
Una vez que llegamos a la conclusión de que los estudios se parecen lo suficiente como para intentar combinarlos debemos tratar de medir esta heterogeneidad para tener un dato objetivo. Para esto, diversos cerebros privilegiados han creado una serie de estadísticos que contribuyen a nuestra cotidiana selva de siglas y letras.
Empezamos con las letras
Hasta hace poco el más famoso era la Q de Cochran, que no tiene nada que ver ni con el amigo de James Bond ni con nuestro amigo Archie Cochrane. Su cálculo tiene en cuenta la suma de las desviaciones entre el resultado del estudio y el resultado global (elevados al cuadrado por aquello de que no se anulen positivas con negativas), ponderando cada estudio según su contribución al resultados global. Parece impresionante pero, en realidad, no es para tanto. En el fondo no es más que una prima aristócrata de la ji-cuadrado.
En efecto, la Q sigue una distribución ji-cuadrado con k-1 grados de libertad (k es el número de estudios primarios). Calculamos su valor, buscamos en la distribución de frecuencias la probabilidad de que la diferencia no se deba al azar y tratamos de rechazar nuestra hipótesis nula (que asume que las diferencias entre estudios son debidas al azar). Pero la Q, a pesar de sus apariencias, tiene una serie de debilidades.
En primer lugar, es un parámetro conservador y debemos siempre tener en cuenta que no significativo no es sinónimo obligatoriamente de ausencia de heterogeneidad: simplemente, no podemos rechazar la hipótesis nula, así que la damos como buena, pero siempre con el riesgo de cometer un error de tipo II y columpiarnos. Por esto, algunos proponen utilizar un nivel de significación de p<0,1 en lugar de la p<0,05 habitual.
Otro fallo que tiene la Q es que no cuantifica el grado de heterogeneidad y, por supuesto, tampoco da razones de las causas que la producen. Y, por si fuera poco, pierde potencia cuando el número de estudios es pequeño y no permite comparar diferentes metanálisis entre sí si el número de estudios es diferente.
Por estos motivos se ha desarrollado otro estadístico que es mucho más celebre en la actualidad: la I2. Este parámetro proporciona una estimación de la variabilidad total entre los estudios respecto a la variabilidad total lo que, dicho de otro modo, es la proporción de la variabilidad debida a diferencias reales entre los estimadores respecto a la variabilidad debida al azar (dicho de forma aún más sencilla, la proporción de variabilidad no debida al azar). Además, es menos sensible a la magnitud del efecto y al número de estudios. También parece impresionante, pero en realidad es otra prima aventajada del coeficiente de correlación intraclase.
Su valor va de 0 a 100%, considerándose habitualmente los límites de 25%, 50% y 75% para delimitar cuando existe una heterogeneidad baja, moderada y alta, respectivamente. La I2 no depende de las unidades de medida de los efectos ni del número de estudios, por lo que sí permite comparaciones con distintas medidas de efecto y entre diferentes metanálisis con diferente número de estudios.
Si encontráis algún estudio con Q pero sin I2, o viceversa, y queréis calcular el que no tenéis, podéis utilizar la siguiente formulilla, donde k es el número de estudios primarios:
Existe un tercer parámetro menos conocido, pero no por ello menos digno de mención: la H2. Esta H2 mide el exceso del valor de Q respecto del valor que esperaríamos obtener si no existiese heterogeneidad. Por tanto, un valor de 1 significa que no hay heterogeneidad y su valor aumenta cuando aumenta la heterogeneidad entre los estudios. Pero su verdadero interés es que permite el cálculo de intervalos de confianza para la I2.
Otras veces los autores realizan un contraste de hipótesis con una hipótesis nula de no heterogeneidad y utilizan una chi ji-cuadrado o algún estadístico similar. En estos casos, lo que proporcionan es un valor de significación estadística. Si la p es < 0,05 se puede rechazar la hipótesis nula y decir que hay heterogeneidad. En caso contrario diremos que no podemos rechazar la hipótesis nula de no heterogeneidad.
En resumen, siempre que veamos un indicador de homogeneidad que represente un porcentaje nos indicará la proporción de variabilidad que no es debida al azar. Por su parte, cuando nos den una “p” habrá heterogeneidad significativa cuando la “p” sea menor de 0,05.
No os preocupéis por los cálculos de Q, I2 y H2. Para eso se usan programas específicos como RevMan o módulos que hacen la misma función dentro de los programas de estadística habituales.
Métodos gráficos para el estudio de la heterogeneidad en el metanálisis
Un punto de atención: recordad siempre que no poder demostrar heterogeneidad no siempre quiere decir que los estudios sean homogéneos. El problema es que la hipótesis nula asume que son homogéneos y las diferencias se deben al azar. Si podemos rechazarla podemos asegurar que hay heterogeneidad (siempre con un pequeño grado de incertidumbre). Pero esto no funciona al revés: si no podemos rechazarla quiere decir simplemente eso, que no podemos rechazar que no haya heterogeneidad, pero siempre habrá una probabilidad de cometer un error de tipo II si asumimos directamente que los estudios son homogéneos.
Por este motivo se han ideado una serie de métodos gráficos para inspeccionar los estudios y comprobar que no hay datos de heterogeneidad aunque los parámetros numéricos digan otra cosa.
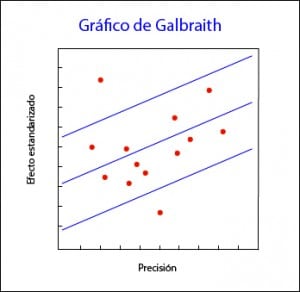
El gráfico de Galbraith puede resultar útil también para detectar fuentes de heterogeneidad, ya que se pueden etiquetar los estudios según diferentes variables y ver como contribuyen a la heterogeneidad global.
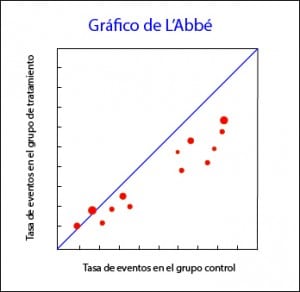
Por encima de la diagonal quedan los estudios con resultado favorable al tratamiento, mientras que por debajo están aquellos con resultado favorable al control. Los estudios suelen representarse con un área proporcional a su precisión y su dispersión indica heterogeneidad. Además, en ocasiones pueden dar información adicional.
Por ejemplo, en el gráfico que os adjunto podéis ver que a riesgos bajos los estudios están en el área del control, mientras que en riesgos altos van hacia la zona favorable al tratamiento. Esta distribución, además de ser sugestiva de heterogeneidad, puede sugerirnos que la eficacia del tratamiento depende del nivel de riesgo o, dicho de otro modo, que tenemos alguna variable modificadora de efecto en nuestro estudio. Una pequeña pega de esta herramienta es que solo es aplicable a metanálisis de ensayos clínicos y cuando la variable dependiente es dicotómica.
Hay que darle a cada uno su peso
Bien, supongamos que hacemos el estudio de heterogeneidad y decidimos que vamos a combinar los estudios para hacer el metanálisis. El siguiente paso es analizar los estimadores del tamaño de efecto de los estudios, ponderándolos según la contribución que cada estudio va a tener sobre el resultado global. Esto es lógico, no puede contribuir lo mismo al resultado final un ensayo con pocos participantes y un resultado poco preciso que otro con miles de participantes y una medida de resultado más precisa.
La forma más habitual de tener en cuenta estas diferencias es ponderar la estimación del tamaño del efecto por la inversa de la varianza de los resultados, realizando posteriormente el análisis para obtener el efecto medio. Para estos hay varias posibilidades, algunas de ellas muy complejas desde el punto de vista estadístico, aunque los dos métodos que se utilizan con más frecuencia son el modelo de efecto fijo y el modelo de efectos aleatorios. Ambos modelos difieren en la concepción que hacen de la población de partida de la que proceden los estudios primarios del metanálisis.
Los dos modelos
El modelo de efecto fijo considera que no existe heterogeneidad y que todos los estudios estiman el mismo tamaño de efecto de la población (todos miden el mismo efecto, por eso se llama de efecto fijo), por lo que se asume que la variabilidad que se observa entre los estudios individuales se debe únicamente al error que se produce al realizar el muestreo aleatorio en cada estudio. Este error se cuantifica estimando la varianza intraestudios, asumiendo que las diferencias en los tamaños de efecto estimados se deben solo a que se han utilizado muestras de sujetos diferentes.
Por otro lado, en el modelo de efectos aleatorios se parte de la base de que el tamaño de efecto varía en cada estudio y sigue una distribución de frecuencias normal dentro de la población, por lo que cada estudio estima un tamaño de efecto diferente. Por lo tanto, además de la varianza intraestudios debida al error del muestreo aleatorio, el modelo incluye también la variabilidad entre estudios, que representaría la desviación de cada estudio respecto del tamaño de efecto medio. Estos dos términos de error son independientes entre sí, contribuyendo ambos a la varianza del estimador de los estudios.
En resumen, el modelo de efecto fijo incorpora solo un término de error por la variabilidad de cada estudio, mientras que el de efectos aleatorios añade, además, otro término de error debido a la variabilidad entre los estudios.
Veis que no he escrito ni una sola fórmula. En realidad no nos hace falta conocerlas y son bastante antipáticas, llenas de letras griegas que no hay quien las entienda. Pero no os preocupéis. Como siempre, los programas estadísticos como RevMan de la Cochrane Collaboration permiten hacer los cálculos de forma sencilla, quitando y sacando estudios del análisis y cambiando de modelo según nos apetezca.
El tipo de modelo a elegir tiene su importancia. Si en el análisis previo de homogeneidad vemos que los estudios son homogéneos podremos utilizar el modelo de efecto fijo. Pero si detectamos que existe heterogeneidad, dentro de los límites que nos permitan combinar los estudios, será preferible usar el modelo de efectos aleatorios.
Otra consideración a realizar es la de la aplicabilidad o validez externa de los resultados del metanálisis. Si hemos utilizado el modelo de efecto fijo será comprometido generalizar los resultados fuera de las poblaciones con características similares a las de los estudios incluidos. Esto no ocurre con los resultados obtenidos utilizando el modelo de efectos aleatorios, cuya validez externa es mayor por provenir de poblaciones de diferentes estudios.
En cualquier caso, obtendremos una medida de efecto medio junto con su intervalo de confianza. Este intervalo de confianza será estadísticamente significativo cuando no cruce la línea de efecto nulo, que ya sabemos que es cero para diferencias de medias y uno para odds ratios y riesgos relativos. Además, la amplitud del intervalo nos informará sobre la precisión de la estimación del efecto medio en la población: cuánto más ancho, menos preciso, y viceversa.
Si pensáis un poco comprenderéis en seguida porqué el modelo de efectos aleatorios es más conservador que el de efecto fijo en el sentido de que los intervalos de confianza que se obtienen son menos precisos, ya que incorpora más variabilidad en su análisis. En algún caso puede ocurrir que el estimador sea significativo si usamos el de efecto fijo y no lo sea si usamos el de efectos aleatorios, pero esto no debe condicionarnos a la hora de escoger el modelo a utilizar. Siempre debemos basarnos en la medida previa de heterogeneidad aunque, si tenemos dudas, también podemos utilizar los dos y comparar los diferentes resultados.
¿Y si hay heterogeneidad?
Una vez estudiada la homogeneidad de los estudios primarios podemos llegar a la desoladora conclusión de que la heterogeneidad es la reina de la situación. ¿Podemos hacer algo? Claro, podemos. Siempre podemos no combinar los estudios o combinarlos a pesar de la heterogeneidad y obtener una medida resumen, pero habrá que calcular también medidas de variabilidad entre estudios y, aun así, no podremos estar seguros de nuestros resultados.
Otra posibilidad es hacer un análisis estratificado según la variable que cause la heterogeneidad, siempre que seamos capaces de identificarla. Para esto podemos hacer un análisis de sensibilidad, repitiendo los cálculos extrayendo uno a uno cada uno de los subgrupos y ver cómo influyen en el resultado global. El problema es que esto deja de lado el verdadero objetivo del metanálisis, que no es otro que el de obtener un valor global de estudios homogéneos.
Los más sesudos en estos temas pueden, por último, recurrir a la metarregresión. Esta técnica es similar a un modelo de regresión multivariante en el que las características de los estudios se usan como variables explicativas y la variable de efecto o alguna medida de la desviación de cada estudio respecto al global se usa como variable dependiente. Hay que hacer, además, una ponderación según la contribución de cada estudio al resultado global y procurar no meter muchos coeficientes al modelo de regresión si el número de estudios primarios no es muy grande. No os aconsejo que hagáis una metarregresión en vuestra casa si no es acompañados de personas mayores.
Nos vamos…
Y ya solo nos quedaría comprobar que no nos faltan estudios sin recoger y presentar los resultados de forma correcta. Los datos de los metanálisis suelen representarse en un gráfico específico que se suele conocer por su nombre en inglés: el forest plot. Pero esa es otra historia…

El meta análisis parece trabajar de forma similar a como lo hace el ANOVA.
Gracias Oma por tu comentario y por leer el blog.
En estadística hay métodos y herramientas que se reutilizan con frecuencia y conexiones entre unas técnicas y otras. Aunque creo que ANOVA y metanálisis son técnicas estadísticas diferentes que se utilizan en contextos diferentes, sí que se podría establecer una relación en el sentido de que resultados de los análisis de ANOVA individuales pueden combinarse a través de un metanálisis para obtener conclusiones más generales y sólidas sobre un tema de interés.
Además, de manera similar a como ANOVA compara la variabilidad dentro de grupos con la variabilidad entre grupos para determinar si hay diferencias significativas entre las medias de varios grupos, el metanálisis valora la variabilidad intraestudios debida al azar y la variabilidad entre estudios debida a diferencias de los mismos, con el objeto de hacer una mejor estimación de la medida de resumen global en la población.
Estoy de acuerdo contigo. De alguna manera, todo esto tiene cierto tipo de conexión.
Saludos
Manolo