Clinical relevance.

We describe how the clinical relevance of the results of a study should be assessed, without being limited only to their statistical significance.
In any epidemiological study, results and validity are always at risk of two fearsome dangers: random bias and systematic bias.
Systematic bias (or systematics errors) are related to study design defects in any of its phases, so we must be careful to avoid them in order to not to compromise the validity of the results.
Random bias is quite different kettle of fish. It’s inevitable and is due to changes beyond our control which occur during the process of measurement and data collection, so altering the accuracy of our results. But do not despair: we can’t avoid randomness, but we can control (within some limits) and quantify it.
Let’s suppose we have measured differences in oxygen saturation between lower and upper extremities in twenty healthy newborns and we’ve came up with an average result of 2.2%. If we repeat the experiment, even in the same infants, what value will we come up with?. In all probability, any value but 2.2% (although it will seem quite similar if we make the two rounds in the same conditions). That’s the effect of randomness: repetition tends to produce different results, although always close to the true value we want to measure.
Random bias can be reduced by increasing the sample size (with one hundred instead of twenty children the averages will be more the same if we repeat the experiment), but we’ll never get rid of it completely. To make things worse, we don’t even want to know the mean saturation’s differences in these twenty, but in the overall population from which they are extracted. How can we get out of this maze?. You’ve got it, using confidence intervals.
Statistical significance
When we establish the null hypothesis of no difference between measuring saturation on the leg or on the arm and we compare means with the appropriate statistical test, p-values will tell us the probability that the difference found is due to chance. If p<0.05 we’ll assume that the probability it is due to chance is small enough to calmly reject the null hypothesis and embrace the alternative hypothesis: it is not the same to measure oxygen saturation on the leg or on the arm. On the other hand, if p is not significant we won’t able to reject the null hypothesis, insomuch us we’ll always think about what if we would have obtained the p-value with 100 children, or even with 1000. p might have reach statistical significance and we might have rejected H0.
If we calculate the confidence interval of our variable we’ll get the range in which the real value is with a certain probability (typically 95%). The interval will inform us about the accuracy of the study. It will not be the same to come up with oxygen saturation’s difference from to 2 to 2.5% than from 2 to 25% (in this case, we should distrust study results no matter it had a five-zero p value).
Clinical relevance
And what if p is non-significant?. Can we draw any conclusions from the study?. Well, that depends largely on the importance of what we are measuring, on its clinical relevance. If we consider as clinically significant a saturation difference of 10% and the interval is below this value, clinical importance will be low no matter the significance of p. But the good news is that this reasoning can also be state in the reverse way: non-statistically significant intervals can have a great impact if any of its limits intersect with the area of clinical importance.
Let’s see some examples in the figure above, in which a difference of 5% oxygen saturation has been considered as clinically significant (I apologize to the neonatologists, but the only thing I know about saturation is that it’s measured by a device that now and then is not capable of doing its task and beeps).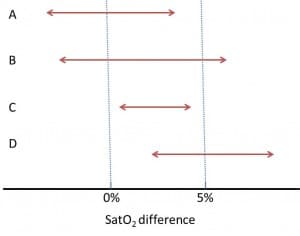
Study A is not statistically significant (its confidence interval intersects with the null effect, which is zero in our example) and, also, it doesn’t seem to be clinically important.
Study B is not statistically significant but it may be clinically important, since its upper limits falls into the clinical relevance’s area. If you’d increase the accuracy of the study (increasing sample size), who assures us that the interval could not be narrower and above the null effect line, reaching statistical significance?. In this case the question is not very important because we are measuring a bit nonsense variable, but think about how the situation would change if we were considering a harder variable, as mortality.
Studies C and D reach statistical significance, but only study D’s results are clinically relevant. Study C shows a statistically significant difference, but its clinical relevance and therefore its interest are minimal.
We’re leaving…
So, you see, there are times that a non-statistically significant p-value can provide information of interest from a clinical point of view, and vice versa. Furthermore, all that we have discussed is important to understand the designs of superiority, equivalence and non-inferiority trials. But that’s another story…
