Tau-squared.

My brother-in-law, who is a private detective, told me the other day about a puzzling crime investigation he had to deal with: several witnesses had seen the suspect, but each described him differently. One said he was tall and blond; another said he was short and dark-skinned; a third insisted he limped, while the fourth swore he ran like an athlete. How is this possible? Did they all see the same culprit, or is there more than one suspect involved?

My brother-in-law quickly understood: the key is to understand that each testimony comes from a different perspective and with its own margin of error. And this is where we connect with our statistical mystery in this post.

When a meta-analysis is performed, the primary studies act like those witnesses: each one provides their own estimate of the effect of an intervention, but not all of them do so in the same way. It is not just that there are differences due to pure chance, but that they are often analyzing slightly different populations. And here comes the random effects model, which not only accepts this variability, but embraces it. What it really tries to assess is not just how dispersed the results of the studies are, but how diverse the reality they are measuring is.

And then comes the tau squared (τ²), which many interpret only a measure of heterogeneity between the studies included in the review. But actually, it goes further: it tells us how the effects we want to estimate vary in the different populations from which those studies come.

Indeed, τ² is not a simple reflection of the inconsistency in the data, but a window into the diversity of the real effects in different contexts. So, like a good detective, instead of getting stuck with the confusion of the testimonies, let’s better understand what they are telling us about the case… before accusing the wrong suspect.

One suspect or several?

As we already know from a previous post, when we want to combine the primary studies of a meta-analysis to calculate the global summary measure, we can adopt two approaches or, in other words, apply two different models.

The first is the fixed effect model. Let’s see the assumption on which it is based.

When we carry out a systematic review with its meta-analysis, our ultimate goal, as in most of our studies, is to estimate the value of a variable in the population, which is inaccessible and, therefore, impossible to measure directly. To do this, we carry out a study with a series of participants, which is nothing more than a sample of that population from which we want to estimate the parameter.

The fixed effect model assumes, as its name indicates, that the effect is the same (fixed) in all the populations from which each of the primary studies of the review comes.

But things get complicated if we take into account that the results of each primary study are also estimates of the population effect and, as they are carried out with a sample of the population from which they come, there is always a margin of error.

In this way, the different studies provide different values ​​of the target variable (although the true effect is the same in all their populations), but these differences are only due to chance, to sampling errors, since the true value of the effect, which we cannot measure directly, is fixed.

Forgive me, but I am going to summarize the above with a small and relatively harmless formula:

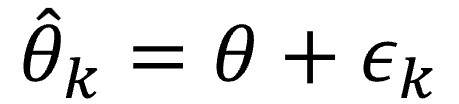
This would be the formula for the k^th study of the review, which attempts to estimate the population effect, represented by the letter θ with the hat (the circumflex accent, the hat, usually means that the parameter is an estimate). This estimate will resemble the unknown real effect in the population, θ, modified by the sampling error of the study, ε_k, our inseparable companion, chance.

Thus, all the studies are similar (they try to estimate the same effect in the population) and the only variation that exists is that which occurs within studies due to chance.

The problem with this model is that it is too simplistic and may not fit well with reality, which is much more complex, in which the populations from which the studies come may not be so homogeneous.

In these cases, it can be assumed that, in addition to the intra-study variations, there will be variations between the different studies that will no longer be due only to chance, but to differences between the different populations. This is the assumption on which the random effects model is based, which attempts to better adjust to the reality of our studies.

The random effects model thus adds another source of variability, due to the fact that the studies do not come from a single population, but from a “universe” of populations, each with its own effect. To put it very simply, the effect is no longer fixed, the same for all, but each population from which each primary study comes will have its own.

Returning to our beloved mathematical notation, in the previous equation we will have to replace the value of the effect (θ, which was fixed) by its new value, which will take into account this new source of variation:

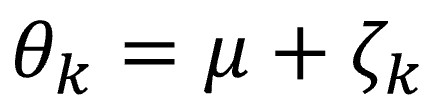
In this case, μ represents the mean of that universe of true effects of the different populations from which the studies come, while ζ_k represents the error of each study in estimating the effect of its population, the variability between the different studies.

If we combine the equations seen so far, we obtain the one for the random effects model, which includes the intra- and inter-study variability:

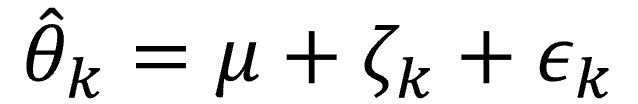
Tau-squared: measuring diversity

Returning to the general approach to meta-analysis, we saw earlier that we cannot simply average the primary results, but rather we have to make a weighted combination of the effects of each study to the final result.

With the fixed-effect model it is simple: it is usually weighted by the inverse of the variance. The result will be that the most precise studies (lower variance) will have a greater weight in the global result.

However, if we use a random-effects model, we will have to include in the weighting a term that considers the variability between studies to calculate the weighting of the studies. This parameter is known as tau-squared (τ²).

Where does this τ² come from? We have already said that the random-effects model assumes the existence of a universe of populations, each with its effect. If we sample a very large number of populations, we can obtain a large number of estimates of the average effect. This is the μ of the formula we saw above. But if we calculate the variance of this set of estimates, do you know what we get? In effect, the value of τ².

Thus, τ² represents nothing more and nothing less than the variability of the effect between different populations.

As you can easily imagine, in practice we cannot make a large number of estimates in a large number of samples, so the problem of how to calculate the value of this parameter arises.

In practice, there are several methods for estimating the value of τ², all of them with mathematics that is sufficiently unpleasant so as not to go into detail in this post. In addition, you already know that statistical programs do it quickly and easily.

The most famous of these methods is the classic DerSimonian-Laird method, easy to calculate, widely used and available in most computer packages, such as the much-acclaimed RevMan. The problem is that its results may be biased if the review has few primary studies and high heterogeneity, so there are currently other methods that may be more suitable.

One of them is the restricted maximum likelihood method, which is more computationally expensive but more accurate and less subject to bias. There is a variant, the maximum likelihood method, which is simpler and faster but not as effective in avoiding bias as its older brother.

Another method is the Paule-Mandel method, which works well, like the previous ones, with continuous variables, but also with binary results. The problem is that it falls flat when the studies are small, especially if there is a large variation in sample size between the studies in the review. Another similar method is the empirical Bayes method, which provides a Bayesian approach, which is usually more complex to implement.

Finally, we should mention the Sidik-Jonkman method, which claims to prevent the risk of false positives, especially when there is a lot of heterogeneity between the studies.

And which one should we use? you may ask. To give some simple recommendations, you can use the restricted maximum likelihood method when the effect is measured with a continuous variable, the Paul-Mandel method when it is a binary variable (unless there is a lot of variation between the sample sizes of the studies), and the Sidik-Jonkman method when you have high heterogeneity and it is a priority to avoid a false positive.

In any case, if what you are looking for is to easily share the results so that other authors can learn about them and even try to replicate them, the classic DerSimonian-Laird method may be a good option.

Tau-squared: the confidence of the unpredictable

Let’s look at one of the uses of τ². We have already said that it quantifies the variance of the distribution of true effects in populations. And, as with any variance, we can take a squared root to obtain τ, the standard deviation of this distribution of effects.

Well, we can combine τ² and the standard error of the summary measure to calculate the confidence interval around the mean value of the effects in the different populations. This is what is known as the prediction interval, which gives us an idea of ​​where the effect would be in new studies that could be added with the same criteria as those of the primary studies in the review.

This interval, which only applies to the summary measure of the meta-analysis, gives us an idea of ​​the confidence we can have about the validity of the result. The more precise (narrower) the interval is and the further away its extremes are from the null value (1 for relative risks and odds ratios, 0 for means difference), the more confident we can be in the overall result obtained.

Authors will have to specify that this is a prediction interval and will represent it by adding two “whiskers” to the diamond of the overall measure of the forest plot.

Heterogeneity is something else

To finish this post, I would like to clarify that, although it is usually represented and discussed as a measure of heterogeneity, τ² is not exactly that.

Heterogeneity is quantified using Cochran’s Q, which is a weighted sum of the squared differences in the overall effect and that of each study, as we saw in a previous post that you can review if you want.

These differences follow a chi-squared distribution with k-1 degrees of freedom (being k the number of studies). Knowing this, we can know what probability there is that the observed differences are due to chance, making the relevant hypothesis test. If the chi-squared value is significant, we conclude that it is very unlikely that the differences are due only to chance, so we assume that there is heterogeneity between the studies.

The τ² is used to quantify this heterogeneity and to make a weighted sum of the results of the studies (together with the variance, which will take into account the variability due to chance) but, strictly speaking, it is not a measure of heterogeneity between studies.

Let’s think about it for a moment. Cochran’s Q and I² assess the dispersion of the results of the primary studies with respect to the overall result obtained by the meta-analysis. For its part, the τ² estimates how the effects of the different populations from which the primary studies come vary with respect to the hypothetical average value of the effect of all these populations.

Obviously, the τ² is closely related to the heterogeneity between studies, but its meaning goes much further.

We’re leaving…

And here we are going to leave it for today.

We have seen the differences between the two most commonly used models to combine the results of the primary studies of a meta-analysis, the fixed effect model (both words are singular) and the random effects model.

We have also seen how to quantify the variability between the different populations that the random effects model supposes, which usually resembles reality more than the simplistic fixed effect model.

Finally, we have reflected on the fact that τ² is, in reality, more than a simple measure of heterogeneity, as it is usually treated. In any case, it is good to provide its value together with the heterogeneity parameters and, even better, to combine these parameters with the prediction interval, since in this way we will be able to better assess to what extent we can trust in the validity of the results of the meta-analysis.

Finally, if we observe that the values ​​of τ² and heterogeneity are high, we must ask ourselves whether the studies are really different or whether there is some black sheep with a very large effect (or a very small one, but with a very large sample size) that may be skewing our results, which brings us to the detection of studies that can act as influencers, as if it were a social network. But that is another story…