Tau-cuadrado.

Mi cuñado, que es detective privado, me contó el otro día la desconcertante investigación de un crimen a la que tuvo que enfrentarse: varios testigos habían visto al sospechoso, pero cada uno lo describía de manera distinta. Para uno, era alto y rubio; para otro, bajito y moreno; un tercero insistía en que cojeaba, mientras que el cuarto juraba que corría como un atleta. ¿Cómo es posible? ¿Vieron todos al mismo culpable o hay más de un sospechoso en juego?

Mi cuñado lo comprendió rápidamente: la clave está en entender que cada testimonio proviene de una perspectiva diferente y con su propio margen de error. Y justo aquí es donde enlazamos con nuestro misterio estadístico en esta entrada.

Cuando se realiza un metanálisis, los estudios primarios funcionan como esos testigos: cada uno aporta su propia estimación del efecto de una intervención, pero no todos lo hacen de la misma manera. No es solo que haya diferencias por puro azar, sino que, a menudo, están analizando poblaciones ligeramente distintas. Y aquí entra en escena el modelo de efectos aleatorios, que no solo acepta esta variabilidad, sino que la abraza. Lo que realmente intenta valorar no es solo qué tan dispersos están los resultados de los estudios, sino qué tan diversa es la realidad que están midiendo.

Y entonces aparece la tau cuadrado (τ²), que muchos interpretan solo como una medida de heterogeneidad entre los estudios incluidos en la revisión. Pero en realidad, va más allá: nos informa de cómo varían los efectos que queremos estimar en las diferentes poblaciones de las que proceden esos estudios.

En efecto, la τ² no es un simple reflejo de la inconsistencia en los datos, sino una ventana a la diversidad de los efectos reales en distintos contextos. Así que, como buen detective, en lugar de quedarnos con la confusión de los testimonios, mejor entendamos qué nos están diciendo sobre el caso… antes de acusar al sospechoso equivocado.

¿Un sospechoso o varios?

Como ya sabemos de una entrada anterior, cuando queremos combinar los estudios primarios de un metanálisis para calcular la medida de resumen global, podemos adoptar dos enfoques o, dicho de otra manera, aplicar dos modelos diferentes.

El primero es el modelo de efecto fijo. Veamos la suposición en que se basa.

Cuando realizamos una revisión sistemática con su metanálisis, nuestro objetivo último, como en la mayoría de nuestros estudios, es estimar el valor de una variable en la población, que es inaccesible y, por tanto, imposible de medir de forma directa. Para ello, realizamos un estudio con una serie de participantes, que no es más que una muestra de esa población de la que queremos estimar el parámetro.

El modelo de efecto fijo supone, como su propio nombre indica, que el efecto es fijo en todas las poblaciones de las que proceden cada uno los estudios primarios de la revisión.

Pero la cosa se complica si tenemos en cuenta que los resultados de cada estudio primario son también estimaciones del efecto poblacional y como se realizan con una muestra de la población de la que proceden, siempre hay un margen de error.

De esta manera, los diferentes estudios proporcionan diferentes valores de la variable objetivo (aunque el efecto verdadero sea el mismo en todas sus poblaciones), pero estas diferencias se deben solo al azar, a los errores de muestreo, ya que el verdadero valor del efecto, que no podemos medir directamente, es fijo.

Me vais a perdonar, pero voy a resumir lo anterior con una fórmula, pequeña y relativamente inofensiva:

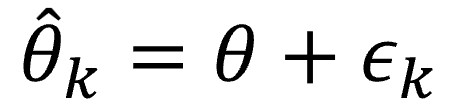
Esta sería la fórmula para el estudio k de la revisión, que trata de hacer una estimación del efecto poblacional, representado con la letra θ con el sombrero (el acento circunflejo, el sombrero, suele significar que el parámetro es una estimación). Esta estimación se parecerá al efecto real desconocido en la población, θ, modificado por el error de muestreo del estudio, ε_k, nuestro inseparable compañero, el azar.

Así, todos los estudios son similares (tratan de estimar el mismo efecto en la población) y la única variación que hay es la que se produce intra-estudios debida al azar.

El problema de este modelo es que es demasiado simplista y puede no ajustarse bien a la realidad, mucho más compleja, en la que las poblaciones de las que proceden los estudios pueden no ser tan homogéneas.

En estos casos, puede asumirse que, además de las variaciones intra-estudios, habrá variaciones entre los diferentes estudios que ya no serán debidas solo al azar, sino a diferencias entre las diferentes poblaciones. Esta es la suposición en la que se basa el modelo de efectos aleatorios, que trata de ajustarse mejor a la realidad de nuestros estudios.

El modelo de efectos aleatorios añade, pues, otra fuente de variabilidad, debida al hecho de que los estudios no proceden de una sola población, sino de un “universo” de poblaciones, cada una con su efecto propio. Por decirlo de forma muy sencilla, el efecto ya no es fijo, para todos el mismo, sino que cada población de la que proceda cada estudio primario tendrá el suyo.

Volviendo a nuestra querida notación matemática, en la ecuación anterior habrá que sustituir el valor del efecto (θ, que era fijo) por su nuevo valor, que tendrá en cuenta esta nueva fuente de variación:

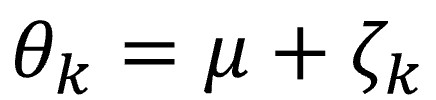
En este caso, μ representa la media de ese universo de efectos verdaderos de las diferentes poblaciones de las que proceden los estudios, mientras que ζ_k representa el error de cada estudio al hacer la estimación del efecto de su población, la variabilidad entre los diferentes estudios.

Si combinamos las ecuaciones vistas hasta ahora, obtendremos la del modelo de efectos aleatorios, que incluye la variabilidad intra y entre-estudios:

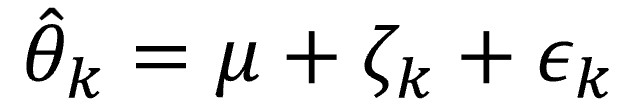
Tau-cuadrado: midiendo la diversidad

Volviendo al planteamiento general del metanálisis, vimos anteriormente que no podemos hacer una media de los resultados primarios sin más, sino que tenemos que hacer una combinación ponderada de los efectos de cada estudio al resultado final.

Con el modelo de efecto fijo es sencillo: se suele ponderar por el inverso de la varianza. El resultado será que los estudios más precisos (menor varianza) tendrán un peso mayor en el resultado final.

Sin embargo, si utilizamos un modelo de efectos aleatorios, tendremos que incluir en la ponderación un término que considere la variabilidad entre-estudios para el cálculo de la ponderación de los estudios. Este parámetro es el que se conoce como tau-cuadrado (τ²).

¿De dónde sale esta τ²? Ya hemos dicho que el modelo de efectos aleatorios supone la existencia de un universo de poblaciones, cada una con su efecto. Si muestreamos un número muy grande de poblaciones, podremos obtener un número grande de estimaciones del efecto medio. Esta es la μ de las fórmulas que vimos más arriba. Pero, si calculamos la varianza de este conjunto de estimaciones, ¿sabéis que conseguimos? En efecto, el valor de la τ².

Así, la τ², representa nada más y nada menos, que la variabilidad del efecto entre las diferentes poblaciones.

Como es fácil de imaginar, en la práctica no podemos hacer un número grande de estimaciones en un número grande de muestras, por lo que surge el problema de cómo calcular el valor de este parámetro.

En la práctica existen varios métodos para estimar el valor de τ², todos ellos con una matemática lo suficientemente antipática como para no entrar en detalles en esta entrada. Además, ya sabéis que los programas estadísticos lo hacen de manera rápida y sencilla.

El más célebre de estos métodos es el clásico de DerSimonian-Laird, fácil de calcular, ampliamente utilizado y disponible en la mayoría de los paquetes informáticos, como el tan aclamado RevMan. Tiene el problema de que su resultado puede estar sesgado si la revisión tiene pocos estudios primarios y alta heterogeneidad, por lo que, en la actualidad, hay otros métodos que pueden ser más adecuados.

Uno de ellos es el método de la máxima verosimilitud restringida, más costoso desde el punto de vista computacional, pero más preciso y menos sujeto a sesgos. Hay una variante que es el método de máxima verosimilitud, más sencillo y rápido, pero no tan eficaz en la evitación de sesgos como su hermano mayor.

 Otro método es el de Paule-Mandel que funciona bien, como los anteriores, con variables continuas, pero también con resultados binarios. El problema es que hace aguas cuando los estudios son pequeños, sobre todo si hay una gran variedad en el tamaño entre los estudios de la revisión. Otro método similar es el de Bayes empírico, que aporta un enfoque bayesiano, que suele ser más complejo de implementar.

Por último, mencionar el método de Sidik-Jonkman, que presume de prevenir el riesgo de falsos positivos, sobre todo cuando existe mucha heterogeneidad entre los estudios.

¿Y cuál tenemos que emplear?, os preguntaréis. Por dar unas recomendaciones simples, podéis usar el de máxima verosimilitud restringida cuando el efecto se mida con una variable continua, el de Paul-Mandel cuando se trate de una variable binaria (salvo que haya mucha variación entre los tamaños muestrales de los estudios), y el de Sidik-Jonkman cuando tengáis alta heterogeneidad y sea prioritario evitar un falso positivo.

En cualquier caso, si lo que buscáis es compartir fácilmente los resultados para que otros autores puedan conocerlos e, incluso, tratar de replicarlos, puede ser una buena opción el clásico de DerSimonian-Laird.

Tau-cuadrado: la confianza de lo impredecible

Vamos a ver una de las utilidades que tiene la τ². Ya hemos dicho que cuantifica la varianza de la distribución de los efectos verdaderos de las poblaciones. Y, como a toda varianza, podemos hacerle una raíz cuadrada para obtener τ, la desviación estándar de esta distribución de efectos.

Pues bien, podemos combinar τ² y el error estándar de la medida resumen para calcular el intervalo de confianza alrededor de valor medio de los efectos en las diferentes poblaciones. Esto es lo que se conoce como intervalo de predicción, que nos da una idea de por donde estaría el efecto en nuevos estudios que pudiesen añadirse con los mismos criterios que los de los estudios primarios de la revisión.

Este intervalo, que solo se aplica a la medida resumen del metanálisis, nos da una idea de la confianza que podemos tener acerca de la validez del resultado. Cuanto más preciso sea (más estrecho) y más lejos estén sus extremos del valor nulo (1 para riesgos relativos y odds ratios, 0 para diferencia de medias), más podremos fiarnos del resultado global obtenido.

Los autores tendrán que especificar que se trata de un intervalo de predicción y lo representarán añadiendo dos “bigotes” al diamante de la medida global del forest plot.

La heterogeneidad es otra cosa

Para ir terminando esta entrada, me gustaría aclarar que, aunque suele representarse y discutirse como una medida de heterogeneidad, la τ² no es exactamente eso.

La heterogeneidad se cuantifica a partir de la Q de Cochran, que es una suma ponderada de las diferencias del efecto global y el de cada estudio elevadas al cuadrado, tal como vimos en una entrada anterior que podéis repasar si queréis.

Estas diferencias siguen una distribución de la ji-cuadrado con k-1 grados de libertad (k es el número de estudios). Sabiendo esto, podemos saber qué probabilidad hay de que las diferencias observadas se deban al azar, haciendo el pertinente contraste de hipótesis. Si el valor de ji-cuadrado es significativo, concluimos que es muy poco probable que las diferencias se deban solo al azar, con lo que asumimos que existe heterogeneidad entre los estudios.

La τ² nos sirve para cuantificar esta heterogeneidad y poder hacer la suma ponderada de los resultados de los estudios (junto con la varianza, que tendrá en cuenta la variabilidad debida al azar) pero, en sentido estricto, no es una medida de heterogeneidad entre los estudios.

Pensémoslo un momento. La Q de Cochran y la I² valoran la dispersión de los resultados de los estudios primarios respecto al resultado global obtenido por el metanálisis. Por su parte, la τ² lo que estima es cómo varían los efectos de las diferentes poblaciones de las que proceden los estudios primarios respecto al hipotético valor medio del efecto de todas esas poblaciones.

Como es lógico, la τ² está íntimamente relacionada con la heterogeneidad entre estudios, pero su significado va mucho más allá.

Nos vamos…

Y aquí lo vamos a dejar por hoy.

Hemos visto las diferencias entre los dos modelos más utilizados para combinar los resultados de los estudios primarios de un metanálisis, el de efecto fijo (en singular las dos palabras) y el de efectos aleatorios.

También hemos visto cómo cuantificar la variabilidad entre las diferentes poblaciones que supone el modelo de efectos aleatorios, que suele parecerse más a la realidad que el simplista modelo de efecto fijo.

Por último, hemos reflexionado sobre el hecho de que la τ² sea, en realidad, más que una simple medida de heterogeneidad, como suele ser tratada. De todas formas, está bien proporcionar su valor junto con los parámetros de heterogeneidad y, aún mejor, combinar estos parámetros con el intervalo de predicción, ya que así podremos valorar mejor hasta que punto podemos confiar en la validez de los resultados del metanálisis.

Por último, si observamos que los valores de τ² y de heterogeneidad son elevados, habrá que preguntarse si los estudios son realmente diferentes o si hay alguna oveja negra con un efecto muy grande (o muy pequeño, pero con un tamaño muestral muy grande) que pueda estar desviando nuestros resultados, lo que nos lleva de la mano al estudio de los estudios que pueden actuar como influencers, como si de una red social se tratase. Pero esa es otra historia…