Umbral diagnóstico.

El otro día fui a una fiesta de disfraces, una de esas donde todos llevan máscaras idénticas. Pensaréis que me divertiría mucho, pero la verdad es que mi felicidad se vio empañada por un pequeño contratiempo: encontrar a mi primo, con el que había quedado allí, entre la multitud de enmascarados.

Por una parte, si me equivocaba de persona, podría acabar saludando efusivamente a un desconocido (¡vaya momento incómodo!). No sabía si arriesgarme a saludar a cualquiera que se pareciese un poco a mi primo para no perder la oportunidad, o esperar hasta estar casi seguro de que era él, aunque eso significase arriesgarme a no encontrarle, aunque ya estuviese allí.

¿Os resulta familiar la situación? Es, básicamente, la eterna lucha que enfrentamos los clínicos entre detectar a tiempo a los enfermos y evitar falsos positivos.

Curiosamente, esta tensión entre actuar rápido o ser prudente ha marcado decisiones históricas. Durante la Segunda Guerra Mundial, los operadores de radar británicos enfrentaban un dilema similar: identificar aviones enemigos a tiempo (evitando ataques) sin alarmar a la población con falsas advertencias. Si bajaban demasiado el umbral de detección, cualquier bandada de aves podría ser confundida con bombarderos alemanes. Si lo subían demasiado, los verdaderos ataques podrían pasar desapercibidos. El equilibrio era una cuestión de vida o muerte.

Y en el mundo de las pruebas diagnósticas, nos enfrentamos a una versión menos dramática, pero igual de incómoda: elegir el punto de corte óptimo en una curva ROC. ¿Deberíamos priorizar identificar todos los casos positivos, aunque eso implique aceptar más falsos positivos? ¿O ser más conservadores y reducir los errores, aunque se nos escapen algunos verdaderos positivos? Al final, como en la fiesta de disfraces o en los radares de la guerra, todo depende de lo que esté en juego.

La curva ROC

Pongamos, por ejemplo, que elaboramos un modelo de regresión logística que nos ofrece la probabilidad de que un sujeto sea positivo frente a una determinada enfermedad. En un caso así, nos enfrentaremos a una decisión clave: ¿en qué punto de corte consideramos un resultado como positivo?

Lo primero que se nos ocurre es fijar este umbral en p = 0,5. De este modo, si la probabilidad es mayor o igual a 0,5, clasificamos al sujeto como positivo; si es menor, como negativo. Sin embargo, este umbral no siempre es el más adecuado, especialmente cuando las categorías están desbalanceadas (la probabilidad de estar sano o enfermo es muy diferente), además de no tener en cuenta el contexto clínico, que nos puede condicionar el mayor o menor riesgo de cometer falsos negativos frente a falsos positivos.

Por ejemplo, si estamos diagnosticando una enfermedad rara como la temible fildulastrosis, usar p = 0,5 podría llevar a perder muchos casos reales (bajos verdaderos positivos y muchos falsos negativos), ya que el modelo tenderá a clasificarlos como negativos. En cambio, en situaciones donde un falso positivo tiene consecuencias graves (como un diagnóstico erróneo que llevaría a tratamientos peligrosos, molestos o muy caros), tal vez queramos un umbral más alto para minimizar estos errores.

Aquí es donde entra en juego la curva ROC (Receiver Operating Characteristic). Esta curva muestra el desempeño global de la prueba al trazar la sensibilidad (verdaderos positivos) frente a la tasa de falsos positivos (1 – especificidad) para diferentes puntos de corte.

El desempeño global de la prueba se estima calculando el área bajo la curva (ABC). Una prueba perfecta tendría una curva que pasa por la esquina superior izquierda (donde habría 100% de sensibilidad y 0% de falsos positivos) y un ABC = 1.

El problema es que las pruebas perfectas no existen, así que este punto máximo, el denominado punto o índice de Youden, se ve desplazado hacia abajo y hacia la derecha. Pensaríamos que el problema está resuelto: elegiremos el punto de corte que marca el índice de Youden, donde se maximizan sensibilidad y especificidad. Pues no, esto tampoco nos soluciona el problema en muchos casos.

En la práctica, el punto óptimo depende de lo que más valoremos según el contexto clínico en el que apliquemos la prueba diagnóstica. Si nos interesa maximizar los verdaderos positivos (que no se quede casi ningún enfermo sin diagnosticar), elegimos un umbral más bajo de probabilidad para considerar el resultado de la prueba como positivo.  El punto de corte se moverá hacia la derecha de la curva, con lo que aumentarán los falsos positivos.

Por el contrario, si lo que queremos es reducir los falsos positivos, elevamos el umbral de probabilidad, con lo que el punto de corte se desplazará hacia la izquierda: menor sensibilidad (se nos escaparán enfermos sin diagnosticar) y menor número de falsos positivos.

El problema es encontrar el umbral perfecto que nos proporcione el equilibrio que deseamos, lo cual puede ser especialmente complicado cuando la prevalencia de la enfermedad que queremos diagnosticar es baja, tal como explicamos en una entrada anterior.

El umbral perfecto, o casi

En definitiva, no existe un punto de corte universalmente óptimo, sino que cada escenario requiere ajustar el umbral en función del equilibrio deseado entre sensibilidad (S) y especificidad (E).

Pero no os engañéis, el umbral perfecto no existe. Siempre habrá que pagar un precio en falsos positivos o negativos. Eso sí, podemos regatear ese precio según nos interese. Vamos a verlo con un ejemplo práctico.

Vamos a jugar un poco con los puntos de corte, utilizando para ello el programa R, de acceso libre. Si queréis ver cómo hago los diferentes cálculos, podéis bajaros el script de este enlace.

Para este ejemplo, voy a utilizar el conjunto de datos Pima.te, del paquete MASS de R. Contiene un registro de 332 mujeres gestantes mayores de 21 años que son evaluadas para un diagnóstico de diabetes gestacional según los criterios de la OMS. Además del diagnóstico de diabetes (sí/no), contiene información sobre el número de gestaciones, glucemia plasmática, presión arterial sistólica, pliegue tricipital, índice de masa corporal, antecedente de diabetes y edad.

En este conjunto de datos hay 109 diabéticas y 223 no diabéticas, lo que supone una prevalencia de diabetes gestacional de 0,33.

Lo primero que hacemos es elaborar un modelo de regresión logística múltiple con el diagnóstico de diabetes (1 = sí, 0 = no) como variable dependiente y el resto como variables independientes. No vamos a preguntarnos si este es el mejor modelo posible, ya que no es el tema de esta entrada y, tal como lo hemos descrito, nos sirve perfectamente para lo que queremos mostrar.

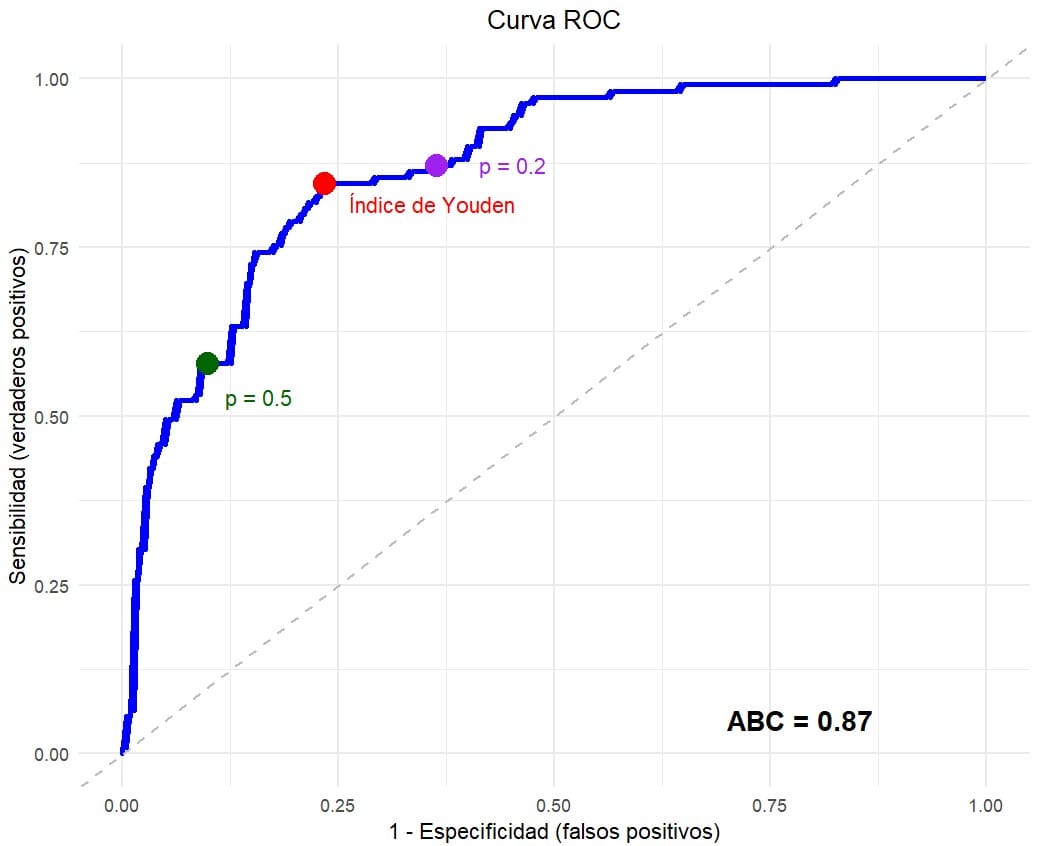
Una vez elaborado el modelo, lo primero que podemos hacer es estimar su desempeño global dibujando la curva ROC y calculando el ABC, que podéis ver en la figura adjunta. Nuestro cálculo nos dice que la prueba tiene un ABC = 0,87, lo que nos sugiere que tiene un buen desempeño en la discriminación entre resultados positivos y negativos. Ignorad, por el momento, los tres puntos que aparecen representados sobre la curva, sobre los que hablaremos a continuación.

El umbral conveniente

Ya estamos listos para empezar el regateo con nuestros puntos de corte. Vamos a empezar con el punto de corte por defecto de la regresión logística, que suele ser considerar positivo el que tiene una probabilidad mayor o igual a 0,5 y negativo el que tiene una probabilidad inferior a este valor. Podéis ver representado este umbral de corte sobre la curva ROC como un punto de color verde.

El modelo de regresión logística que hemos construido nos da la probabilidad de que cada participante pertenezca a la categoría 1 de la variable dependiente o, dicho de forma más sencilla, de que sea diabética. Si elegimos el punto de corte p = 0,5, estaremos marcando este umbral de probabilidad de 0,5 para considerar la prueba como positiva (será negativa si la probabilidad es menor de ese valor).

Así, nos vamos al conjunto de datos y miramos quiénes son o no diabéticas y qué predice el modelo si considera como diabética a la que tenga un valor de probabilidad de serlo (según el modelo) mayor o igual a 0,5. Con esto, podemos calcular la tabla de contingencia y los valores de S, E, verdaderos positivos (VP), verdaderos negativos (VN), falsos positivos (FP), falsos negativos (FN) y la exactitud diagnóstica (la proporción de pacientes correctamente clasificadas). Lo podéis ver en la primera tabla de la figura siguiente.

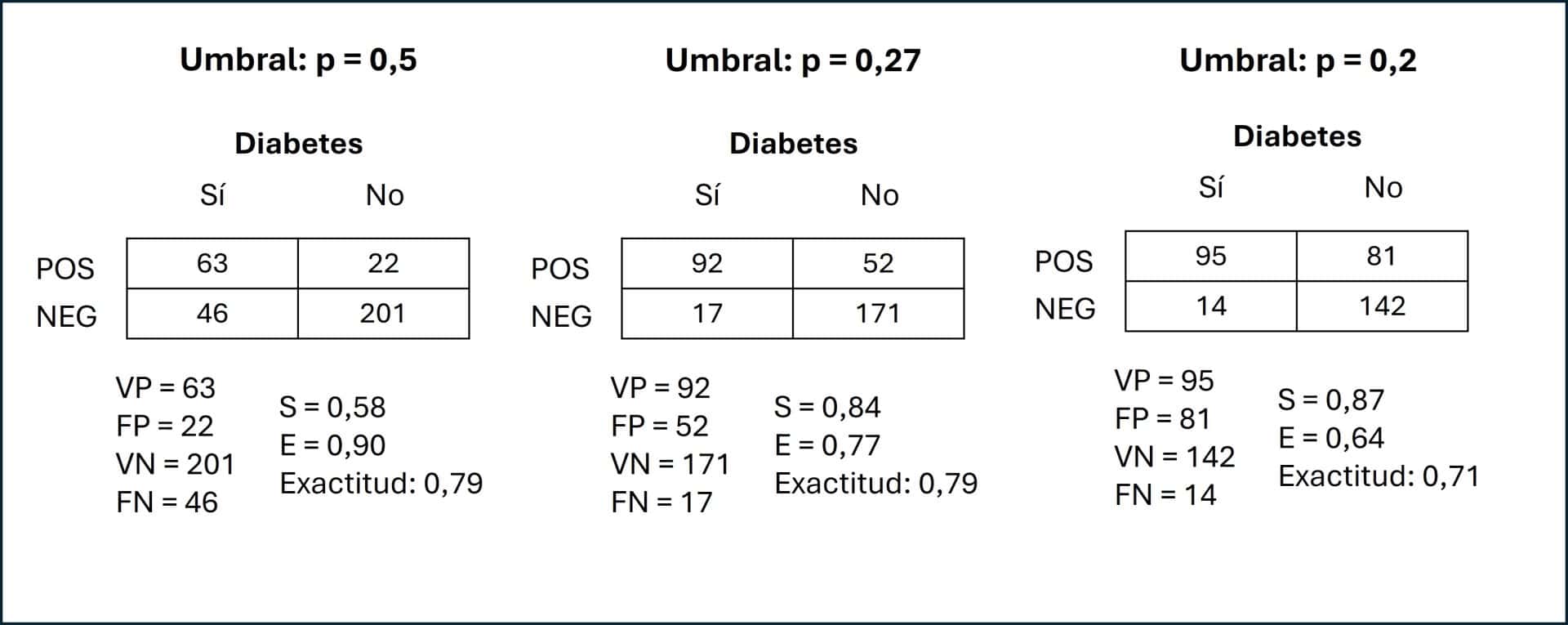
Podemos ver que el 79% de las pacientes están bien diagnosticadas, con una S = 0,58 y una E = 0,90. Aunque la exactitud diagnóstica y la E no son malas, la S es un poco baja para nuestro gusto, lo que se traduce en 46 gestantes que vamos a dejar sin diagnosticar y 22 diagnósticos falsamente positivos.

Yo diría que este umbral no nos conviene mucho, pero ya podíamos imaginarlo. La prevalencia de diabetes en el conjunto de datos es de 0,33, así que este punto de corte nos penaliza la sensibilidad de la prueba.

Vamos a ver qué pasa con el punto de Youden, que maximiza S y E y que veis representado en la curva en color rojo. Este punto equivaldría a elegir un valor de probabilidad mayor o igual a 0,27 para considerar el resultado del modelo como positivo (categoría 1: diabetes). Podéis ver la tabla de contingencia en el centro de la figura anterior.

Como nos hemos movido hacia la derecha sobre la curva ROC, esperaremos una mejora de la S, con un aumento de los FP. Efectivamente, en la tabla observamos una S = 0,84, una E = 0,77 y un total de 52 FP. Lo bueno es que ya solo dejamos a 17 gestantes diabéticas sin diagnosticar (frente a las 46 de la tabla anterior).

En mi opinión, este umbral de corte sería más adecuado para este escenario. Yo diría que es peor dejar una diabética sin diagnosticar que tener que realizar la prueba para confirmar el diagnóstico en los FP (aunque este es un criterio subjetivo que depende del que tenga que establecer el umbral).

Es más, dejar 17 gestantes diabéticas sin diagnosticar me sigue pareciendo demasiado, así que me muevo un poco más hacia la derecha de la curva y elijo un umbral de probabilidad de 0,2, marcado en color púrpura. Fijaos ahora en la tercera tabla de contingencia.

Como era de esperar, la S sube un poco, hasta 0,87, y los FN se quedan solo en 14 totales. El precio que hay que pagar es un aumento de los FP hasta 81. Habrá que valorar riesgo, costes y demás, pero yo diría que entre este y el punto de Youden estaría el umbral óptimo para este escenario.

Nos vamos…

Y aquí vamos a dejar los puntos de corte por hoy.

Hemos visto cómo la elección del punto de corte puede modificar de manera importante el rendimiento de una misma prueba diagnóstica aplicada en un mismo escenario clínico.

Me interesa que, antes de despedirnos, nos fijemos en un detalle que me parece interesante.

La curva ROC y el ABC representan el rendimiento global de la prueba para clasificar correctamente enfermos y sanos. Si os fijáis, solo hemos calculado un ABC, aunque hayamos calculado múltiples valores de S y E para distintos puntos de corte. Además, la exactitud diagnóstica es prácticamente la misma para todos los puntos de corte (hay pequeñas diferencias debidas a errores de redondeo).

Esto es lógico, porque estos parámetros indican solo el rendimiento global, por lo que no son los únicos a tener en cuenta al elegir la utilidad de una determinada prueba en un escenario específico. Puede ocurrir que curvas con un ABC elevada tengan un rendimiento menor en algunos escenarios, sobre todo cuando la prevalencia de la enfermedad a diagnosticar es muy baja.

Claro que en estos casos no hay que despreciar la prueba de entrada. Siempre podemos jugar con el umbral de probabilidad de corte para adaptar el rendimiento a nuestros intereses y aplicar alguna otra herramienta para estos casos de categorías diagnósticas muy desbalanceadas, como es el caso de la razón de enriquecimiento de la precisión. Pero esa es otra historia…