La distribución beta.

Hace ya algún tiempo os conté el aprieto en el que se vio mi primo cuando tuvo que dar una fiesta y él era el encargado de hacer el postre. Aunque se sabía una receta muy buena, el pastel solo le salía bien el 50% de las veces que lo hacía y, claro, quería saber cuántos pasteles cocinar para estar razonablemente seguro de tener uno en condiciones para sus invitados.

Pues resulta que ahora soy yo el que me veo en esa tesitura, así que aquí estoy dándole vueltas al asunto, para no quedar mal con mis invitados. Mi primo recurrió a la probabilidad binomial para estimar que, haciendo 5 pasteles, tenía una probabilidad de casi el 97% de cocinar, al menos, un pastel comestible. Pero a mí me sigue pareciendo mucho riesgo, así que he pensado que sería mucho más seguro contratar un cocinero profesional.

Contratar a un cocinero no debería ser complicado, así que busqué uno que afirmaba que le salen estupendos el 80% de los pasteles que hace. Los que me conocéis sabéis que soy de naturaleza desconfiada, así que quise ver si eso era verdad.

Le di los ingredientes, le metí en la cocina y le pedí que cocinase 10 pasteles. Y aquí es donde comenzaron de verdad los problemas, porque solo 6 de los 10, el 60%, estaban decentes, mientras que los 4 restantes fueron una verdadera catástrofe culinaria.

El pobre cocinero trata de convencerme de que no es más que un simple golpe de mala suerte. Todos tenemos días malos: un error en la receta, un horno caprichoso, un ingrediente en mal estado. Pero también existe una posibilidad más inquietante: que el cocinero haya exagerado sobre sus habilidades. O incluso peor: que, directamente, me haya mentido.

¿Cómo podemos saber si solo tuvo un mal día o si, en realidad, su promedio de pasteles buenos es más bajo de lo que prometió? Aquí es donde entra en juego la estadística. Así como mi primo recurrió a la probabilidad binomial para solucionar su problema, en esta ocasión podemos usar la función beta para estimar la verdadera probabilidad de éxito del cocinero.

Seguid leyendo y trataremos de averiguar si el cocinero es un mentiroso o si, simplemente, ha tenido un día de mala suerte. La incertidumbre está servida, y vamos a calcularla.

El planteamiento binomial del problema

Vamos a empezar por lo más sencillo para intentar comprender cómo podemos averiguar si nuestro cocinero dice la verdad.

Si afirma que el 80% de sus pasteles salen buenos, eso quiere decir que el 80% de sus pasteles salen buenos. Ni más ni menos. ¿Y cómo será el próximo pastel? La respuesta es fácil, habrá un 80% de que sea bueno y un 20% de que vaya a la basura. En resumen: esto es como lo del gato de Schrödinger, que no sabemos si está vivo o muerto hasta que abrimos la caja. En este caso, hasta que probamos el pastel.

Dejando de lado el problema de la decoherencia cuántica, podemos decir sin miedo a equivocarnos que, cuántos más pasteles haga, más probable será que al menos uno de ellos salga bueno. Así, podemos saber la probabilidad de poder contar con un pastel comestible sabiendo el número de intentos que hará el cocinero. Para ello, aplicamos la fórmula para el cálculo de probabilidad binomial.

Si me lo permitís, la fórmula para calcularlo es la siguiente:

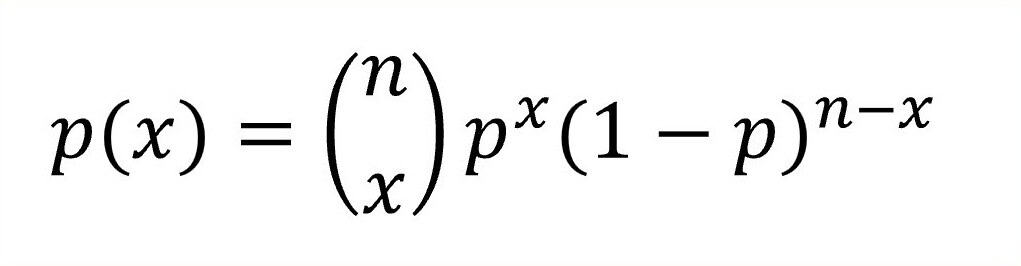
En esta fórmula, n es el número de pasteles que se cocinan, x es el número de pasteles que salen buenos y p es la probabilidad de que un pastel determinado salga bueno.

Este cocinero presume de una tasa de éxitos del 80%. ¿Cuál es la probabilidad de que, cocinando 10 pasteles, 8 o más de ellos salgan buenos? Podemos sustituir los valores en la fórmula anterior o, mejor, utilizar un programa estadístico o una calculadora para obtener el resultado.

Yo he escrito el comando dbinom(8, size = 10, prob = 0.8) en R y me dice que la probabilidad de obtener exactamente 8 pasteles buenos es del 30%. Pero a mí no me importa, e incluso me quedo más tranquilo, si salen 8 o más de los 10.

Para ello, introduzco el comando pbinom(7, size = 10, prob = 0.8, lower.tail = FALSE), obteniendo un valor de probabilidad de casi el 68%. O sea, que no hay garantía de que siempre haya 8 o más de cada 10 pasteles buenos. Eso solo pasará en el 68% de las veces que sometamos al cocinero a la prueba de cocinar 10 pasteles.

Hasta ahora la razón parece inclinarse de parte del cocinero. Es posible que diga la verdad y haya tenido un mal día, después de todo.

Pero como posible no es lo mismo que probable, nos gustaría saber qué probabilidad hay de que, si no miente, obtenga un porcentaje de éxitos tan bajo. La respuesta nos la da una distribución de probabilidad diferente de la binomial, la distribución beta.

La distribución beta

Para situarnos bien, cuando decimos que esperamos que el cocinero consiga 8 pasteles buenos cocinando 10, estamos asumiendo que dice la verdad y que su tasa de éxitos global es del 80%.

Pero vamos a contemplar la situación desde otro punto de vista. ¿Es posible que con otras tasas de éxito diferentes al 80% sea probable obtener 8 pasteles buenos? Esto podría ocurrir con tasas de éxito más bajas, en cuyo caso podría ser que el cocinero fuese un mentiroso.

Para responder a esta pregunta, podríamos empezar a imaginar un montón de situaciones posibles y solucionarlas con otro montón de cálculos con la distribución binomial, pero, en su lugar, vamos a recurrir a la distribución de probabilidad beta, que nos va a permitir hacerlo de forma más directa y sencilla.

Con la distribución beta podemos estimar la verosimilitud de diferentes tasas de éxito para un determinado valor de éxitos y fracasos. Rizando el rizo, podemos decir que la distribución beta muestra las probabilidades de cada probabilidad de éxito, dados un número de éxitos y de fracasos determinados.

Al ser una distribución de probabilidad, la distribución beta nos mostrará una curva entre los valores de x de 0 y 1, con un área bajo la curva global igual a 1. Para calcular la probabilidad de un rango determinado de probabilidad de éxito, tendremos que calcular el área bajo la curva para ese rango.

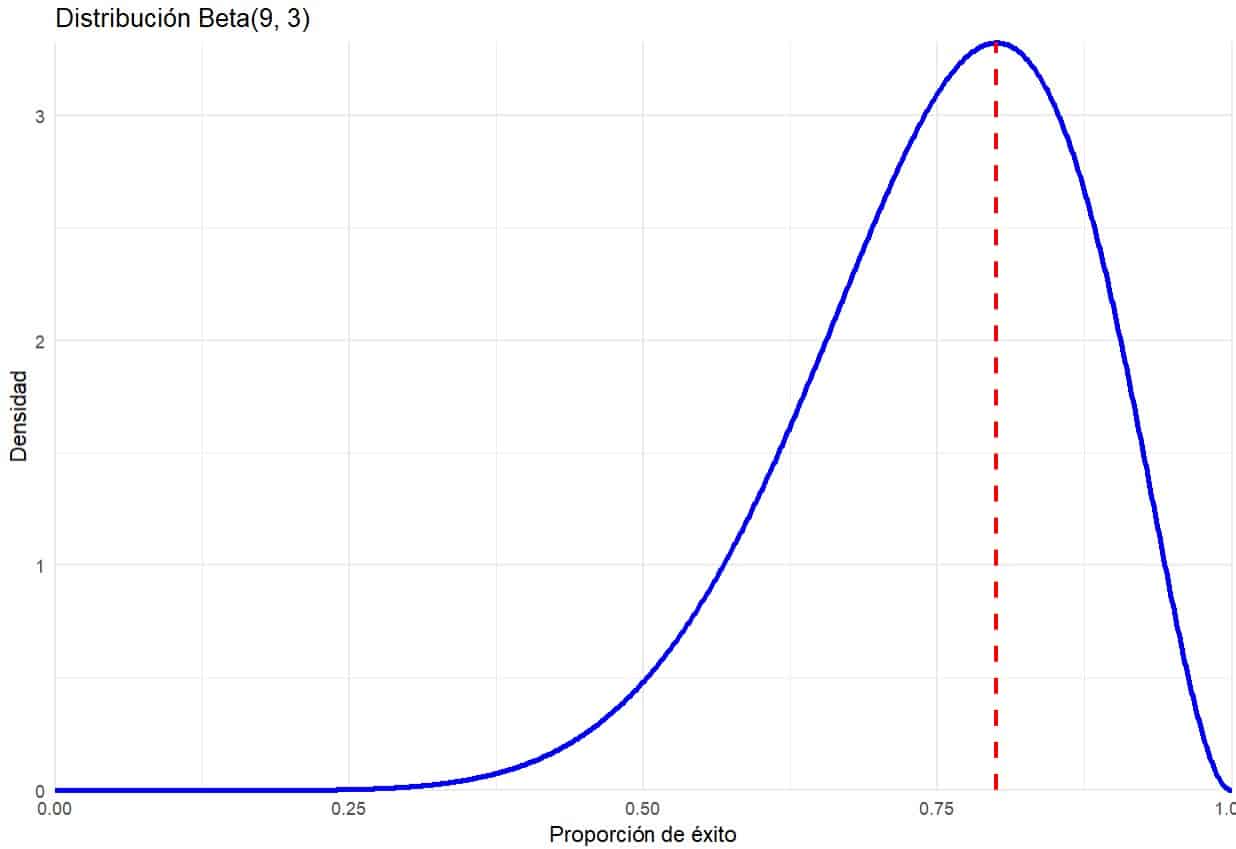
Como la mayoría de las funciones de densidad, la de la distribución beta es lo suficientemente antipática como para que no la pongamos en esta entrada, pero sí os puedo decir que se basa en dos parámetros: alfa, que es el número de éxitos más 1, y beta, que es el número de fracasos más 1. Podemos utilizar la función dbeta() de R para calcularla y representarla gráficamente, tal como podéis ver en la figura.

Podéis ver que, para 8 éxitos de 10 intentos, la tasa de éxito con mayor verosimilitud es, en efecto, la del 80%, tal como afirma el cocinero. Pero ya sabemos que, al tratarse de una función continua, para calcular probabilidades tenemos que integrar el área bajo la curva en un determinado intervalo.

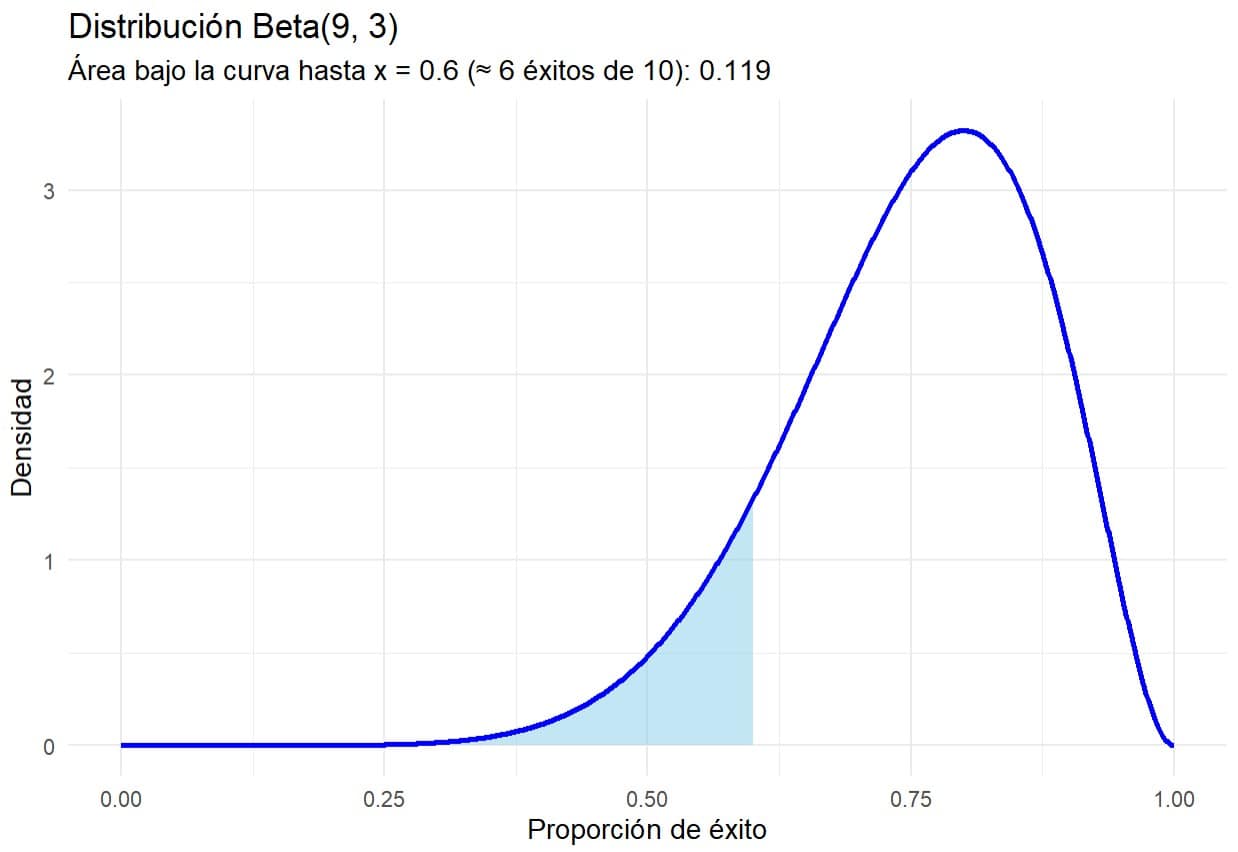
Como nuestro cocinero solo tuvo 6 éxitos cuando le hicimos la prueba, podemos pedirle a R que nos calcule la probabilidad de obtener 6 o menos éxitos si fuese verdad que la tasa de éxitos fuese del 80%. Podéis ver el área representada en la segunda figura.

El área sombreada en azul indica la probabilidad de que un cocinero con una tasa de éxito del 80%, obtenga 6 éxitos o menos en una prueba de cocinar 10 pasteles. El valor de probabilidad es, redondeando, de un 12%. La verdad es que es baja, pero no demasiado. Es posible que el cocinero diga la verdad y solo haya tenido un mal día. Para tener más seguridad, tendríamos que repetir más pruebas o hacer cocinar más pasteles en cada prueba.

Claro que otra opción sería pensar en otro postre diferente más seguro. A este paso, la fiesta me va a salir bastante cara.

Nos vamos…

Y así nos quedamos, mirando esos 6 pasteles buenos de 10 y preguntándonos si este chef es un artista incomprendido o un farsante con delantal.

Gracias a la función beta, podemos no solo estimar cuál podría ser la verdadera habilidad pastelera del cocinero, sino también expresar esa incertidumbre de forma razonada. ¿Es probable que su tasa real sea del 80%? ¿O más bien del 60%… o incluso menos?

Al final tendremos que repetir más pruebas para irnos haciendo una idea de la capacidad del cocinero. Esto es, en esencia, lo que hace la estadística bayesiana: actualizar nuestras creencias a medida que obtenemos nuevos datos, ayudándonos a afinar esa intuición con algo más de rigor. Pero esa es otra historia…