Bayes’ theorem.

We describe the concept of conditional probability and the development of Bayes’ theorem, used to calculate the conditional probability of an event.
Today we are going to see another of those examples where intuition about the value of certain probabilities plays tricks on us. And, for that, we will use nothing less than Bayes’ theorem, playing a little with conditioned probabilities. Let’s see step by step how it works.
What is the probability of two events occurring? The probability of an event A occurring is P(A) and that of B, P(B). Well, the probability of the two occurring is P(A∩B), which, if the two events are independent, is equal to P(A) x P(B).
Imagine that we have a die with six faces. If we throw it once, the probability of taking out, for example, a five is 1/6 (one result among the six possible). The probability to draw a four is also 1/6. What will be the probability of getting a four, once in the first roll we get a five? Since the two runs are independent, the probability of the combination five followed by four will be 1/6 x 1/6 = 1/36.
Conditional probability
Now let’s think of another example. Suppose that in a group of 10 people there are four doctors, two of whom are surgeons. If we take one at random, the probability of being a doctor is 4/10 = 0.4 and that of a surgeon is 2/10 = 0.2. But if we get one and know that he is a doctor, the probability that he is a surgeon will no longer be 0.2, because the two events, being a doctor and a surgeon, are not independent. If you are a doctor, the probability that you are a surgeon will be 0.5 (half the doctors in our group are surgeons).
When two events are dependent, the probability of occurrence of the two will be the probability of occurrence of the first, once the second occurs, by the probability of occurrence of the second. So the P(surgeon) = P(surgeon|doctor) x P(doctor). We can generalize the expression as follows:
P(A∩B) = P(A|B) x P(B), and changing the order of the components of the expression, we obtain the so-called Bayes rule, as follows:
P(A|B) = P(A∩B) / P(B).
The P(A∩B) will be the probability of B, once A is produced, by the probability of A = P(B|A) x P(A). On the other hand, the probability of B will be equal to the sum of the probability of occurrence B once A is produced plus the probability of occurring B without occurring A, which put in mathematical form is of the following form:
P(B|A) x P(A) + P(B|Ac) x P(Ac), being P(Ac) the probability of not occurring A.
If we substitute the initial rule for its developed values, we obtain the best known expression of the Bayes theorem:
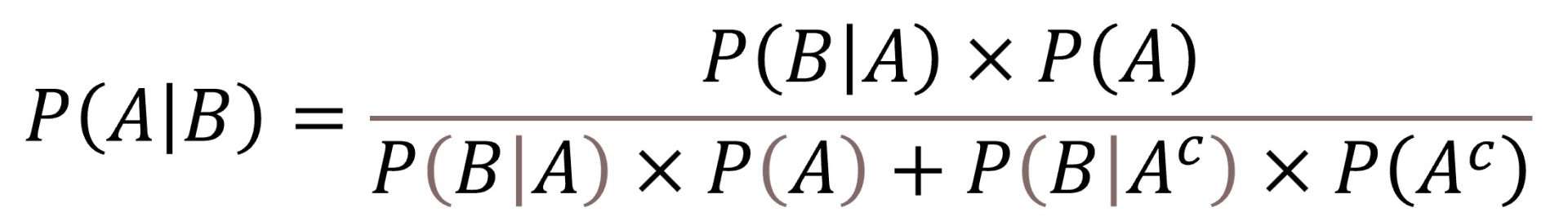
Let’s see how the Bayes theorem is applied with a practical example. Consider the case of acute fildulastrosis, a serious disease whose prevalence in the population is, fortunately, quite low, one per 1000 inhabitants. Then, the P(F) = 0.001.
Let’s see an example
Luckily we have a good diagnostic test, with a sensitivity of 98% and a specificity of 95%. Suppose now that I take the test and it gives me a positive result. Do I have to scare myself a lot? What is the probability that I actually have the disease? Do you think it will be high or low? Let’s see.
A sensitivity of 98% means that the probability of giving positive when having the disease is 0.98. Mathematically, P(POS|F) = 0,98. On the other hand, a specificity of 95% means that the probability of a negative result being healthy is 0.95. That is, P(NEG|Fc) = 0.95. But what we want to know is neither of these two things, but we really look for the probability of being sick once we test positive, that is, P (F|POS).
To calculate it, we have only to apply the theorem of Bayes:
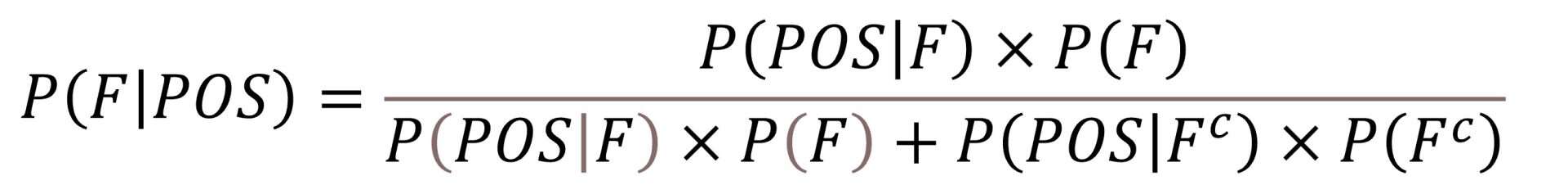
Then we replace the symbols with their values and solve the equation:
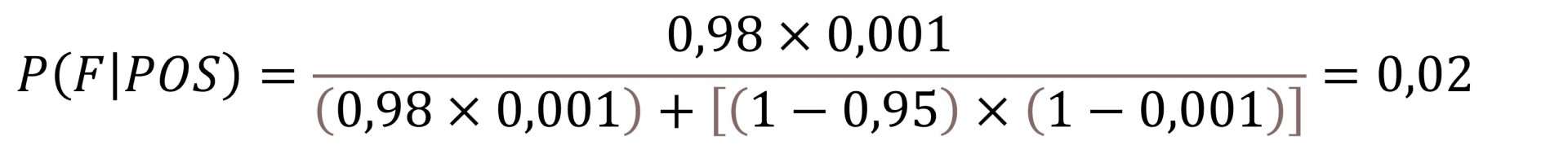
So we see that, in principle, I do not have to scare a lot when the test gives me a positive result, since the probability of being ill is only 2%. As you see, much lower than intuition would tell us with such a high sensitivity and specificity. Why is this happening? Very simple, because the prevalence of the disease is very low. We are going to repeat the experiment assuming now that the prevalence is 10% (0,1):
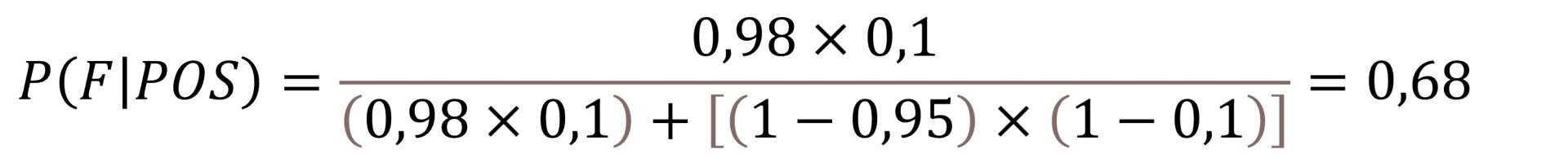
As you see, in this case the probability of being ill if I give positive rises to 68%. This probability is known as positive predictive value which, as we can see, can vary greatly depending on the frequency of the effect we are studying.
We’re leaving…
And here we leave it for today. Before closing, let me warn you not to seek what the fildulastrosis is. I would be very surprised if anyone found it in a medical book. Also, be careful not to confuse P (POS|F) with P (F|POS), since you would make a mistake called reverse fallacy or fallacy of transposition of conditionals, which is a serious error.
We have seen how the calculation of probabilities gets somewhat complicated when the events are not independent. We have also learned how unreliable predictive values are when the prevalence of the disease changes. That is why the likelihood ratios were invented, which do not depend so much on the prevalence of the disease that is diagnosed and allow a better overall assessment of the power of the diagnostic test. But that is another story…
