Clinical relevance.

Clinical relevance should guide us when assessing the results of a study. For this, we will use confidence intervals.
We, the so-called human beings, tend to be too categorical. We love to see things in black and white, when the reality is that life is neither black nor white, but manifest itself in a wide range of grays. Some people think that life is rosy or that the color lies in the eye of the beholder, but do not believe it: life if gray colored.
And, sometimes, this tendency to be too categorical leads us to very different conclusions about a particular topic depending on the white or black eye that the beholder has. So, it’s not uncommon to observe opposing views on certain topics.
And the same can happen in medicine. When there’s a new treatment and it starts running papers about its efficacy or toxicity, it’s not uncommon to find similar studies in which the authors come to very different conclusions. In many times this is due to the effort we do to see things in black or white, drawing categorical conclusions based on parameters like statistical significance, the value of p. Actually, data in many cases don’t say so different things, but we have to look at the range of grays provided to us by confidence intervals.
As I imagine you do not understand quite well what the heck I’m talking about, I’ll try to explain myself better and to give an example.
Not everything is black or white
You know that we can never ever prove the null hypothesis. We can only be able or unable to reject it (in this last case we assume that it’s true, but with a probability of error). This is why when we study the effect of an intervention we state the null hypothesis that the effect does not exist and we design the trial to give us the information about whether or not we can reject it. In case of rejecting it, we assume the alternative hypothesis that says that the effect of the intervention exists. Again, always with a probability of error; this is the p-value or statistical significance.
In short, if we reject the null hypothesis we assume that the intervention has an effect and if we cannot reject it we assume the effect doesn’t exist. Do you realize?: black or white. This so simplistic interpretation doesn’t consider all the grays related to important factors such us clinical relevance, the precision of the estimation or the power of the study.
Clinical relevance: use confidence intervals
In a clinical trial it is usual to provide the difference found between the intervention and control groups. This is a punctual estimation but, as we have performed the trial with a sample from a population, the right thing is to complement the estimate with a confidence interval that provides the range of values that includes the true value in the inaccessible population with a certain probability or confidence. By convention, confidence is usually set at 95%.
This 95% value is usually chosen because we also often use a statistical significance level of 5%, but we must not forget that these are arbitrary values. The great quality of confidence intervals, opposite to p-values, is that no dichotomous conclusions (the kind of white or black) can be drawn.
A confidence interval is not statistically significant when it intersects the line of no effect, which is 1 for relative risks and odds ratios and 0 for absolute risks and mean differences. If you just look at the p-value you can only conclude if the interval reached or not statistical significance, coming up sometimes to very different conclusions with very similar intervals.
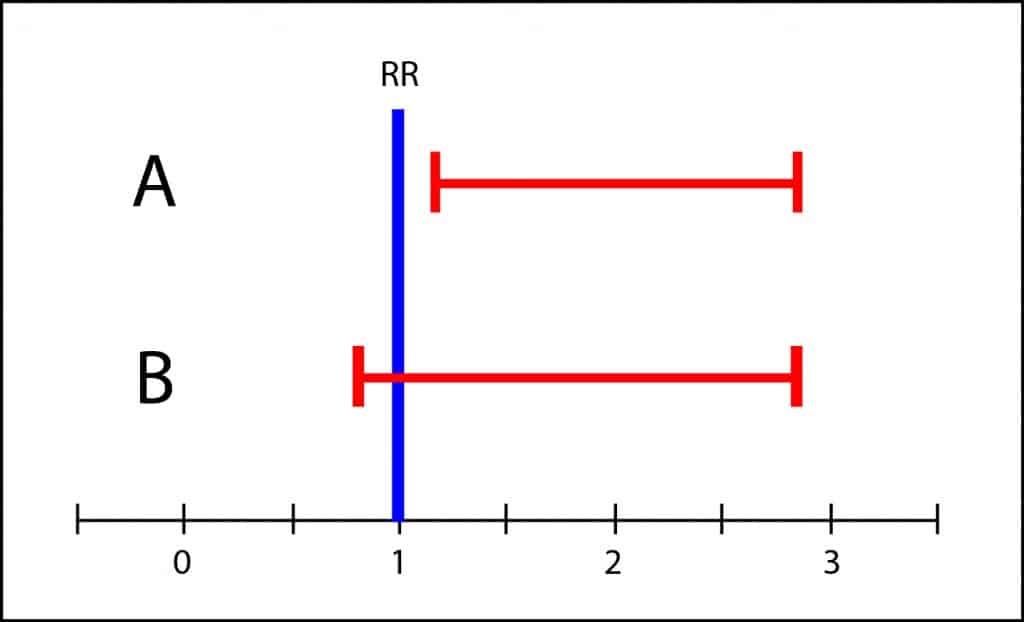
However, the interval of B covers from slightly less than 1 to about 3. This means that the population’s value may be any value in the interval. It could be 1, but it could be also 3, so it’s not impossible that toxicity in the intervention group could be three times greater than in the control group. If the side effects were serious, it wouldn’t be appropriate to recommend the treatment until more conclusive studies with more precise intervals were available. This is what I mean by the scale of grays and the clinical relevance of results. It is unwise to draw black or white conclusions when there’s overlapping of confidence intervals.
So better follow my advice. Pay less attention to p-values and always seek the information about the possible range of effect provided by confidence intervals. Don’t settle for statistical significance and assess the clinical relevance of the results.
We’re leaving…
And that’s all for now. We could talk more about similar situations but when dealing with efficacy studies, or superiority or non-inferiority studies. But that’s another story…
