Analysis of variance (ANOVA).

Analysis of variance (ANOVA) is the test used to compare the differences among more than two means of a quantitative variable.
At least when it comes to contrast of means.
Let’s suppose we want to know if a population of Eskimos eats an amount of seal meat above a certain value. We can calculate the average in a sample, estimate its population’s confidence interval and check whether or not it includes that average value.
Let’s suppose now that we have two populations of Eskimos and we want to know if there’s any difference in their consumption of seal meat. We just have to calculate the means and to do a simple Student’s t test to compare the means. We could also calculate the confidence intervals and check if there’s any overlapping.
Analysis of variance (ANOVA)
But, what if we have three or more populations? Well, it’s not useful to do a Student’s t test neither to compare the intervals. In these cases, we have to use a technique with the misleading name of analysis of variance (ANOVA). And I say misleading name because it compares means, not variances. However, it compares means based on the way data vary, following a rather ingenious reasoning. Let me try to explain it with the help of a real life example.
As in a joke from my childhood, we have five French, five Spanish and five Italians (jokes used to have a Frenchman, an Italian and a Spanish, but little variance we could analyze with so few people). We ask these 15 people how many liters of wine do they drink per month, obtaining the distribution you can see in the table.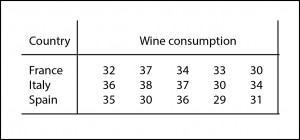
If we calculate the mean values of each group we’ll see that French drink 33.2 liter per month, Italians 35 and Spanish 32.2. Does this mean that French are more drunk than Italians, and Italians more than Spanish?. Well, we cannot know knowing only the means. Even if we have chosen samples that are representatives of their populations, there’s always the possibility that the differences are due to pure chance. So, as always, we have to do a hypothesis testing to find out.
As first step we set the null hypothesis that there are no real differences among the three groups and that the differences observed are due to chance. The alternative hypothesis, meanwhile, says that there are differences among the three groups. So, under the assumption of the null hypothesis, we’ll do the analysis of variance of one factor, which would be the country of origin.
Decomposing the variance
Mean wine consumption of our 15 drunkards is 33.5 liters per month. Assuming the null hypothesis is true, if we take one of them at random, from any country, his expected consumption will be 33.5. However, it is easy to understand that the majority of subjects drawn at random will have a value different than the expected mean. The value of that individual can be decompound into three parts: the global mean, the variation due to the country of origin and the variance due to chance. If you let me give you a little formula, it would be as follows:
x = mean + effect due to the country + random error effect
If the null hypothesis is true and there’re no differences among groups, the variation due to the country will be very small (similar to random variation), whereas if it is false, this variation will be greater. Think now about the value of the quotient country/random error. If there’re not differences among groups (the null is true), the quotient will equal 1 or less than 1. But if the groups have different means, this quotient will equal more than 1, the greater than 1 the wider the differences among groups are, whereas random error will always be more or less the same.
Well, we’re almost there. We know that variance is the average sum of the squares of the distance of each value from the mean. Remember that we squared the differences to avoid negative ones cancel out positive ones.
This variance can be decomposed into the two components we have already explained: the variance among groups (called sum of squares) and the variance by chance (called squares residuals).
Total squares sum = squares sum by group + squares residuals.
The sum of squares
I’m not going to show you the formulas to calculate these sums of squares, although they are not very complex and the example that we are seeing can be solve easily we a simple calculator. There is no point. Any statistical program calculates these sums of squares effortlessly.
And once we have these sums of squares is when the magic of numbers shows up, because it happens that the ratio between squares by group and residuals (country/random) follows a known probability distribution, which is none other than Snedecor’s F with groups-1, n-groups degrees of freedom.
If we calculate it (I’ve done it using the R’s command aov), we’ll come up with an F-value of 1.14. The probability of obtaining this F-value with these degrees of freedom is 0.35. As it is greater than 0.05, we cannot reject the null hypothesis, so we have no choice but to conclude that French, Italian and Spanish are just equally drunks.
We’re leaving…
I’ll make just a couple of comments before finishing this post. First, before to do this type of analysis, we have to check that three conditions are fulfilled: the samples must be independent, they must follow a normal distribution and they have to have equal variances (which is known with the friendly name of homocedasticity). We have assumed the three conditions.
Second, if we had gotten an F-value with p<0.05 and we had rejected the null hypothesis we could had said that there were differences among groups but, between what groups?. First thing that comes to one’s mind is to take the groups by pairs and to do a contrast with the two means, but this cannot be done just like that. The more pairs you compare, the greater the likelihood of committing a type I error and finding a significant difference just by chance, because global significances changes when comparing the means in pairs.
To do that we should have to use other techniques that take into account this effect, such us the Bonferroni’s or Tukey’s tests. But that’s another story…
