Confounding in cohort studies.

Confounding in cohort studies can be controlled by stratifying and calculating an adjusted risk measure.

Sometimes, we cannot help confounding factors getting involved in our studies, both known and unknown. These confounding variables open a backdoor through which our data can slip, making those measures of association between exposure and effect that we estimate not to correspond to reality.

Confounding in cohort studies

During the phase of analysis it is often used techniques as stratification or regression models to measure the association adjusted by the confounding variable. But we can also try to prevent confusion in the design phase. One way is to restrict the inclusion criteria in accordance with the confounding variable. Another strategy is to select controls to have the same distribution of confounding variable than the intervention group. This is what is known as pairing.

Pairing

Suppose we want to determine the effect of smoking on the frequency of laryngeal cancer in a population distribution that you see in the first table. We can see that 80% of smokers are men, while only 20% of non-smokers are. We invented the risk of cancer in men is 2%, but rises to 6% for smokers. For its part, the risk in women is 1%, reaching 3% if they smoke. So, although all of them will double the risk if they practice the more antisocial of the vices, men always have twice the risk than women (while being equal the exposure to tobacco between the two sexes, because men smokers have six times more risk than non-smoker women). In short, sex acts as a confounding factor: influencing the likelihood of exposure and the likelihood of the effect, but is not part of the causal sequence between smoking and cancer of the larynx. This would be taken into account when analyzing and calculating the adjusted relative risk by Mantel-Haenszel technique or using a logistic regression model.

Let’s see another possibility, if we know the confounding factor, which is trying to prevent its effect during the planning phase of the study. Suppose we start from a cohort of 500 smokers, 80% out of them are men and 20% are women. Instead of randomly taking 500 non-smokers controls, we include in the unexposed cohort one non-smoker man per each smoker man in the exposed cohort, and the same with women. We will have two cohorts with a similar distribution of the confounding variable and, of course, also similar in the distribution of the remaining known variables (otherwise we could not compare them).

Risk ratio

Have we solved the problem of confusion? Let’s check it out.

We see the contingency table of our study with 1000 people, 80% men and 20% women in both groups exposed and unexposed. As we know the risk of developing cancer by gender and smoking status, we can calculate the number of people we expect to develop cancer during the study: 24 men smokers (6% of 400), eight non-smoking men (2% of 400), three women smokers (3% of 100) and one non-smoker women (1% of 100).

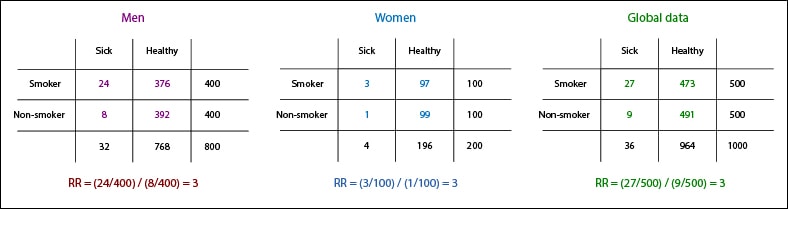
With these data we can build the contingency tables, global and stratified by gender, we expect to find at the end of follow-up. If we calculate the measure of association (in this case, the relative risk) in men and women separately we see that coincides (RR = 3). Plus, it’s the same risk as the global cohort, so it seems we have managed to close the back door. We know that in a cohort study, matching the confounding factor allows us to counteract its effect.

Odds ratio

Now suppose that instead of a cohort study we conduct a case-control study. Can we use the pairing? Of course we can, who’s going to stop us? But there is one problem.

If we think about it, we realize that pairing with cohorts influences both the exposure and the effect. However, in case-control studies, forcing a similar distribution of confounding affects only its influence on the effect, not the one that has over exposure. This is so because homogenizing according to the confounder we also do it according to other related factors, among other, the exposition itself. For this reason, pairing doesn’t guarantee closing the back door in case-control studies.

Someone does not buy it? Let’s assume that we have 330 people with laryngeal cancer (80% male and 20% female). To do the study, we selected a group of similar controls from the same population (what is called a case-control study nested in a cohort study).

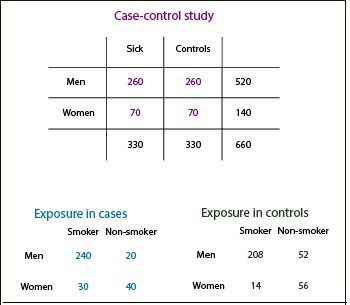
We know the number of expose and non-exposed from data we gave at the beginning of the general population, knowing the risk of cancer arising by gender and exposure to tobacco. In addition, we can also build the table of controls, since we know the percentage of exposure to tobacco by sex.

Finally, with the data from these three tables we can build the contingency tables for the overall study and those for men and women.

In this case, the suitable measure of association is the odds ratio, which has a value of three for men and women, but is 2.18 for the overall study population. Thus we see that they do 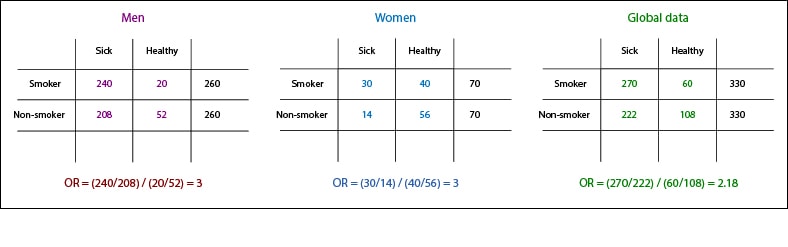not match, which is telling us that we have not completely escaped from the effect of the confounder even though we used the technique of pairing to select the control group.

We’re leaving…

So pairing cannot be used in case-control studies? Yes, yes it can, although the analysis of the results to estimate the extent of adjusted association is a little different. But that is another story…