Stratification.

Stratification is one of the techniques to study the effect of confounding and effect modifiers variables on risk measures.
Who has not heard this sentence a lot of times? Although it’s quite famous, it’s strange that its origin is not well known. Some say it was an occurrence of Julius Caesar, but there seems to be no written evidence to prove it. Others say it was an inspiration of Machiavelli, much given to fuck his neighbors up to obtain personal gain.
I think it’s likely that the award is for neither of them and that the phrase concerned is one more of the vast cultural heritage of ours, the so-called human-beings. What is not in doubt, however, is that it forms the core of a useful strategy for solving problems of some complexity. The problem is divided into smaller parts which are resolved more easily and then these solutions are used to build the complex solution of the initial problem.
Confounding factor
Do you remember the study about tobacco and coronary disease when we speak of confounding? We demonstrate that the effect of the confounding variable was masking the true effect of tobacco on the disease. Well, let’s divide to conquer.
To do this we will use one of the techniques that exist to estimate the effect of the confounding variable: stratification. This consists in creating subgroups from the initial sample, so that each subgroup is free of the confusion produced by the factor. Once this is done, we estimate separate measures of association and, if they are not equal (due to the confounding variable), calculate the estimate of the adjusted association by the factor by which we have stratified (the confusion).
When the confounding variable is not continuous (e.g., male or female) it’s very easy to stratify. However, if the confounder is a continuous variable, such as age, it can be difficult to decide how many strata we need. As much strata we made, less confusion we’ll have, although it’ll be more difficult to obtain useful information from too small strata. And conversely, if there’re few strata we’ll run the risk of not to adjust well the estimate of the measure of association.
Stratification
So I myself am quite sloppy and do not want to do a lot of numbers, I’m going to put the example stratifying into two age groups: older and younger than 50 years.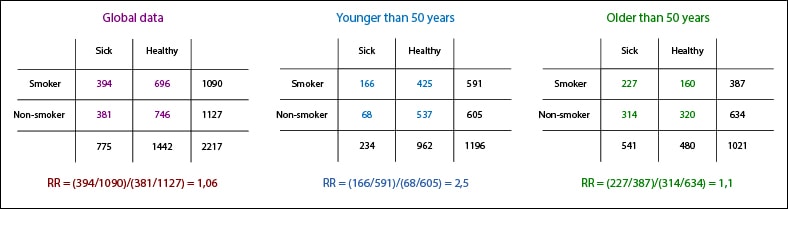
This method weights in a combined way the three factors of the contingency table that reflect the information about exposure and effect: the frequency of effect in exposed and unexposed, the relative sizes of the comparison groups and the overall size of each stratum. Of course, these two gentlemen explain this with a huge equation you’re going to forgive me for not to put it here. Simply, let’s see how the new adjusted RR is calculated.
To calculate the weighted risk in exposed, rather than dividing the number of exposed patients by total exposed as normally would (166/591, for under 50 years), we divide by the total of the stratum and multiplied by the total unexposed as follows:
- Younger than 50 years: Re = 166 x (605/1196) = 83.97.
- Older than 50 years: Re = 227 x (634/1021) = 140.95.
In a similar way, we calculate the weighted risk in non-exposed multiplying the non-exposed who are sick by the total number of exposed and divide it by the total of the stratum:
- Younger than 50 years: Ro = 68 x (591/1196) = 33.60.
- Older than 50 years: Ro = 314 x (387/1021) = 119.01.
Finally, we add the weighted risks in exposed and divide it by the sum of the weighted risks in non-exposed, obtaining the adjusted RR:
aRR = (83,97+140,95) / (33,60+119,01) = 1,47.
It means that the risk of developing coronary heart disease is approximately 50% greater if you smoke, regardless of age.
This simple calculation is much more unfriendly if we are not so shoddy and divide the sample into a greater number of strata. And imagine if the contingency tables get complicated. Of course, that is what computers, calculators, and statistical programs are for; they do all this in a jiffy, we don’t know whether effortless or not, but without any claim.
We’re leaving…
However, there are other methods to calculate the estimate of the adjusted association. The most fashionable now is logistic regression. With the computers actually available to any of us, a paper that doesn’t analyze this problem by applying a regression model is going to get only dirty looks. But that is another story…
