Modifier of effect.

Modifier of effect takes place when the magnitude of a variable interferes with the effect of the exposure on the result.

In this post we will give another twist to the issue of the variables that can disturb the harmonious relationship of the couple formed by exposure and effect, so that all those dirty minds waiting else reading the title can move to the next result of Google, for sure who match what they were looking for.

Confounding variable

We saw that there exist confounding variables that are related to the effect and the exposure and how they can alter our estimates of the measures of association if these variables are not distributed evenly among the study groups. We talk about our backdoor, how to avoid it and how close it both in cohort and in case and control studies.

Modifier of effect

But sometimes the effect of exposure on the outcome studied is not always the same and can vary in intensity as the value or the level of a third variable is changed. As was the case with confounding, we observe it better stratifying the results for analysis, but in these cases is not due to the uneven distribution of the variable, but the effect of exposure is actually modified by the magnitude of this variable, which is called modifying variable or interaction effect.

Naturally, it is essential to distinguish between confounding and interaction variable. The effect of the confounding variable depends on its distribution among the study groups. In experimental studies, this distribution may vary according to the distribution occurred during randomization, so a variable can act as confounder in one trial and not in another. However, in observational studies they always exert their effect, as they are associated both with the exposure and the effect. When we find a confounding variable our goal is to control its effect and estimate an adjusted measure of association.

On the other hand, effect modifier variables represent characteristics of the relationship between exposure and effect whose intensity depends on the ménage à trois created by the interaction of this third variable. If you think about it, in the event that there’s a modification of effect we’ll not be interested in calculating an adjusted measure of association, as we could do with the Mantel-Haenszel test, because it wouldn’t be representative of the overall action of exposure on effect. Neither is good idea to do the simple arithmetic average of the measures of association we observe in each stratum. In any case what we have to do is to describe it and not try to control it, as we do with confounding variables.

Stratification

Before we can say that there is an effect modifier variable we must discard that the observed differences are due to chance, confounding or bias of our study. Observing the confidence intervals of the estimated measures can help to rule out chance, as it will be more unlikely if the intervals do not overlap. We can also calculate whether differences among strata are statistically significant, using the appropriate test according to the design of the study.

And can we estimate an overall measure of the influence of exposure on the effect that takes into account the existence of an interaction variable?. Of course we can, does anyone doubt it?.

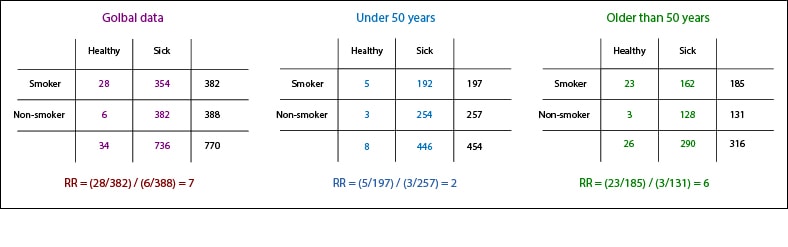
Perhaps the easiest way is to calculate a standardized measure. To do so we compare two different measures, one which assumes that each element of each stratum has the risk of the exposed and another which assumes the same but in non-exposed. Doing so we estimate a measure of the association in the global standard population we have set. Confused?. Let’s see an example. We’re going to continue boring you to exhaustion with poor smokers and their coronary artery disease. In the first table are the results of a study that I just invented over smoking and myocardial infarction.

We see that, overall, smokers have seven times higher risk of suffering infarction than non-smokers (relative risk, RR = 7). Let’s assume that smokers and nonsmokers have a similar age distribution, but that if we break down the data into two age groups the risks are different. The RR under 50 years is 2, compared to the older than 50, whose risk of heart attack is three times higher for smokers than for non-smokers.

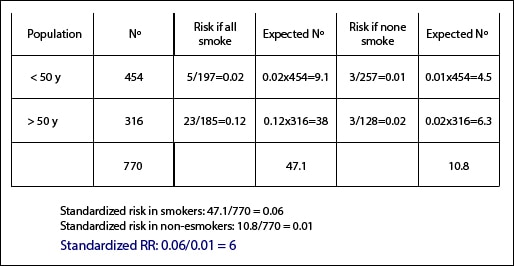
We will calculate two measures of association, one assuming that everyone smokes and the other assuming none smokes. In younger than 50 years, the risk of myocardial infarction if all smoke is 5/197 = 0.02. If we have 454 people less than 50, the expected number of infarctions would be 454×0.02 = 9.1. The risk in non-smokers would be 3/257 = 0.01, so we expect to find 0.01×454 = 4.5 cases of infarction in non-smokers.

We do the same calculations with the older than 50 and we add the total number of people (770), the total number of heart attacks in smokers (47.1) and nonsmokers (10.8). The standardized risk in smokers in this population is 47.1 / 770 = 0.06. The standardized risk in nonsmokers, 10.8 / 770 = 0.01. Finally, we calculate the standardized RR: 0.06 / 0.01 = 6. This means that, globally, smoking increases six time the risk of myocardial infarction, but do not forget that this result is valid only for this standard population and it would probably not for a different population.

We’re leaving…

Just one more thing before finishing. As with the analysis of confounding variables, the analysis of effect modifiers can also be done by regression, introducing an interaction coefficient in the obtained equation to correct the effect of the modifier. Moreover, these coefficients are very useful to us because their statistical significance serves to distinguish between confusion and interaction. But that is another story…