Association measures.

The measures of association are described and how it is preferable to use absolute measures of impact over relative ones.
If you have at home a bottle of wine that has gotten a bit chopped up, take my advice and don’t throw it away. Wait until you receive one of those scrounger visits (I didn’t mention any brother-in-law!) and offer it to drink it. But you have to combine it with a rather strong cheese. The stronger the cheese is, the better the wine will taste (you can have other thing with any excuse). Well, this trick almost as old as the human species has its parallels in the presentation of the results of scientific work.
Association measures
Let’s suppose we conduct a clinical trial to test a new antibiotic (call it A) for the treatment of a serious infection that we are interesting in. We randomize the selected patients and give them the new treatment or the usual one (our control group), as chance dictates. Finally, we measure in how many of our patients there’s a treatment failure (how many has the event we want to avoid).
Thirty-six out of the 100 patients receiving drug A presented the event to avoid. Therefore, we can conclude that the risk or incidence of presenting the event in the exposed group (Ie) is 0.36 (36 out of 100). Moreover, 60 out of the 100 controls (we call them the non-exposed group) presented the event, so we quickly compute the risk or incidence in non-exposed (Io) is 0.6.
Risk ratio
We see at first glance that risks are different in each group, but as in science we have to measure everything, we can divide risks between exposed and 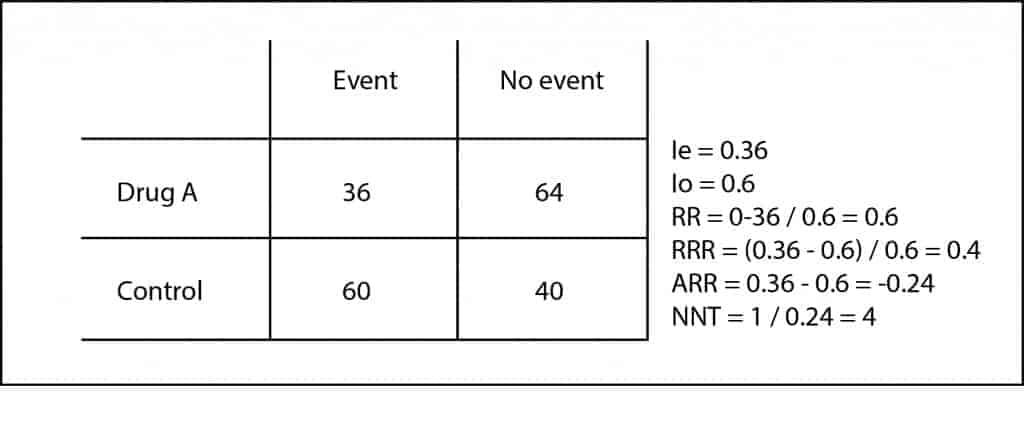
In our case, RR = 0.36 / 0.6 = 0.6. It’s easier to interpret the RR when its value is greater than one. For example, a RR of 2 means that the probability of the event is two times higher in the exposed group. Following the same reasoning, a RR of 0.3 would tell us that the event is two-thirds less common in exposed than in controls.
Risk reduction
But what interests us is how much decreases the risk of presenting the event with our intervention, in order to estimate how much effort is needed to prevent each event. So we can calculate the relative risk reduction (RRR) and the absolute risk reduction (ARR). The RRR is the difference in risk between the two groups with respect to the control group (RRR = [Ie-Io] / Io). In our case its value is 0.6, which mean that the tested intervention reduces the risk by 60% compared to standard therapy.
Number needed to treat
The ARR is simpler: it’s the subtraction between the exposes’ and control’s risks (ARR = Ie – Io). In our case is 0.24 (we omit the negative sign; that means that for every 100 patients treated with the new drug, it will occur 24 less events than if we had used the control therapy. But there’s more: we can know how many patients we have to treat with the new drug to prevent each event just using a rule of three (24 is to 100 as 1 is to x) or, more easily remembered, calculating the inverse of the ARR.
Thus, we come up with the number needed to treat (NNT) = 1 / ARR = 4.1. In our case we would have to treat four patients to avoid an adverse event. The clinical context will tell us the clinical relevance of this figure.
Use absolute measures
As you can see, the RRR, although technically correct, tends to magnify the effect and don’t clearly quantify the effort required to obtain the result. In addition, it may be similar in different situations with totally different clinical implications. Let’s look at another example. Suppose another trial with a drug B in which we get three events in the 100 patients treated and five in the 100 controls.
If you do the calculations, the RR is 0.6 and the RRR is 0.4, as in our previous example, but if you compute the ARR you’ll come up with a very 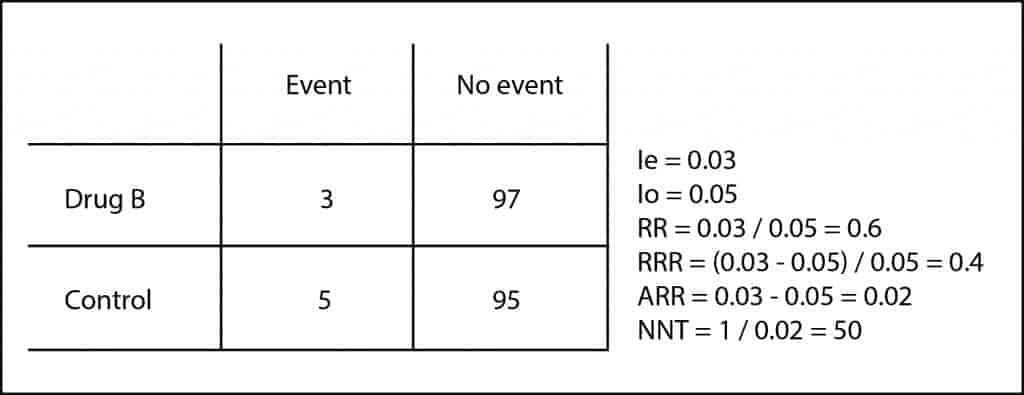
So, at this point, let me advice you. As the data needed to calculate RRR are the same than to calculate the easier ARR (and NNT), if a scientific paper offers you only the RRR and hide the ARR, distrust it and do as with the brother-in-law who offers you wine and strong cheese, asking him to offer an Iberian ham pincho. Well, I really wanted to say that you’d better ask your shelves why they don’t give you the ARR and compute it using the information from the article.
Of course, all these measurements can be easily calculated using one of the calculators available on the Internet.
We’re leaving…
One final thought to close the topic. There’s a tendency and confusion when using or analyzing another measure of association employed in some observational studies: the odds ratio. Although they can sometimes be comparable, as when the prevalence of the effect is very small, in general, odd ratio has other meaning and interpretation. But that’s another story…
