Confounding variable.

A confounding variable is associated with the exposure and the effect without being part of the cause-effect chain between the two.
I wish I had a time machine!. Think about it for a moment. We should not have to work (we would have won the lottery several times), we could anticipate all our misfortunes, always making the best decision … It would be like in the movie “Groundhog Day”, but without acting the fool.
Counterfactuals outcomes
Of course if we had a time machine that worked, there would be occupations that could disappear. For example, epidemiologists would have a hard time. If we wanted to know, imagine, if the snuff is a risk factor for coronary heart disease we only would’ve to take a group of people, tell them not to smoke and see what happened twenty years later. Then we would go back in time, require them to smoke and see what happen twenty years later and compare the results of the two tests. How easy, isn’t it?. Who would need an epidemiologist and all his complex science about associations and study designs?. We could study the influence of exposure (the snuff) on the effect (coronary heart disease) comparing these two potential outcomes, also called counterfactual outcomes (pardon the barbarism).
However, not having a time machine, the reality is that we cannot measure the two results in one person, and although it seems obvious, what it actually means is that we cannot directly measure the effect of exposure to a particular person.
So epidemiologists resort to study populations. Normally in a population will be exposed and unexposed subjects, so we can try to estimate the counterfactual effect of each group to calculate what would be the average effect of exposure on the population as a whole. For example, the incidence of coronary heart disease in nonsmokers may serve to estimate what would have been the incidence of disease in smokers if they had not smoked. This enables that the difference in disease between the two groups (the difference between its factual outcomes), expressed as the applicable measure of association, is an estimate of the average effect of smoking on the incidence of coronary heart disease in the population.
All that we have said requires a prerequisite: counterfactual outcomes have to be interchangeable. In our case, this means that the incidence of disease in smokers if they had not smoked would have been the same as that of nonsmokers, who have never smoked. And vice versa: if the group of non-smokers had smoked they would have the same incidence than that observed in those who are actually smokers. This seems like another truism, but it’s not always the case, since in the relationship which exists between effect and exposure frequently exist backdoors that make counterfactual outcomes of the two groups not interchangeable, so the estimation of measures of association cannot be done properly. This backdoor is what we call a confounding factor o confounding variable.
Confounding variable
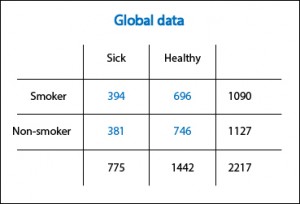
Let’s clarify a bit with a fictional example. In the first table I present the results of a cohort study (that I have just invented myself) that evaluates the effects of smoking on the incidence of coronary heart disease. The risk of disease is 0.36 (394/1090) among smokers and 0.34 (381/1127) among nonsmokers, so the relative risk (RR, the relevant measure of association in this case) is 0.36 / 0.34 = 1.05. I knew it!. As Woody Allen said in “Sleeper”!. The snuff is not as bad as previously thought. Tomorrow I go back to smoking.
Sure?. It turns out that mulling over the matter, it just occurs to me that something may be wrong. The sample is large, so it is unlikely that chance has played me a bad move. The study does not apparently have a substantial risk of bias, although you can never completely trust. So, assuming that Woody Allen wasn’t right in his film, there is only the possibility that there’s a confounding variable implicated altering our results.
Requirements for a confounding variable
The confounding variable must meet three requirements. First, it must be associated with exposure. Second, it must be associated with the effect of exposure independently of the exposure we are studying. Third, it should not be part of the chain of cause-effect relationship between exposure and effect.
This is where the imagination of researcher comes into play, which has to think what may act as a confounder. To me, in this case, the first that comes to mind is age. It fulfills the second point (the oldest are at increased risk of coronary heart disease) and third (no matter how the snuff is, it doesn’t increase your risk of getting sick because it makes you older). But, does it fulfill the first condition?. Is there an association between age and the fact of be a smoker?. It turns out that we had not thought about it before, but if this were so, it could explain everything. For example, if smokers were younger, the injurious effect of snuff could be offset by the “benefit” of younger age. Conversely, the benefit of the elderly for not smoking would vanish because of the increased risk of older age.
Stratification
How can we prove this point?. Let’s separate the data of younger and older than 50 years and let’s recalculate the risk. If the relative risks are different, you will probably want to say that age is acting as a confounding variable. Conversely, if they are equal there will be no choice but to agree with Woody Allen.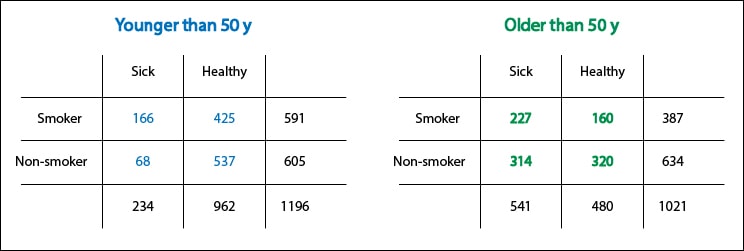
With this example we realize how important it is what we said before about counterfactual outcomes being interchangeable. If the age distribution is different between exposed and unexposed and we have the misfortune of that age is a confounding variable, the result observed in smokers will no longer be interchangeable with the counterfactual outcome of nonsmokers, and vice versa.
Controlling confounding variables
Can we avoid this effect?. We cannot avoid the effect of a confounding variable, and this is even a bigger problem when we don’t know that it can play its trick. Therefore it’s essential to take a number of precautions when designing the study to minimize the risk of its occurrence and having backdoors which data squeeze through.
One of these is randomization, with which we will try that both groups are similar in terms of the distribution of confounding variables, both those known and unknown. Another would be to restrict the inclusion in the study of a particular group as, for instance, those less than 50 years in our example. The problem is that we cannot do so for unknown confounders. Another third possibility is to use paired data, so that for every young smoker we include, we select another young non-smoker, and the same for the elderly. To apply this paired selection we also need to know beforehand the role of confounding variables.
We’re leaving…
And what do we do once we have finished the study and found to our horror that there is a backdoor?. First, do not despair. We can always use the multiple resources of epidemiology to calculate an adjusted measure of association which estimate the relationship between exposure and effect regardless of the confounding effect. In addition, there are several methods for doing the analysis, some simpler and some more complex, but all very stylish. But that’s another story…