Histograma y diagrama de barras.

Se revisan las diferencias entre el diagrama de barras, útil para representar variables cualitativas, y el histograma, para cuantitativas.
¿En qué se parecen un huevo y una castaña?. Si disparamos nuestra imaginación podemos dar algunas respuestas tan absurdas como rebuscadas. Los dos son de forma más o menos redondeada, los dos pueden servir de alimento y los dos tienen una cubierta dura que encierra la parte que se come. Pero, en realidad, un huevo y una castaña no se parecen en nada aunque queramos buscar similitudes.
Lo mismo les pasa a dos herramientas gráficas muy utilizadas en estadística descriptiva: el diagrama de barras y el histograma. A primera vista pueden parecer muy similares pero, si nos fijamos bien, existen claras diferencias entre ambos tipos de gráficos, que encierran conceptos totalmente diferentes.
Tipos de variables
Ya sabemos que hay distintos tipos de variables. Por un lado están las cuantitativas, que pueden ser continuas o discretas. Las continuas son aquellas que pueden tomar un valor cualquiera dentro de un intervalo, como ocurre con el peso o la presión arterial (en la práctica pueden limitarse los valores posibles debido a la precisión de los aparatos de medida, pero en la teoría podemos encontrar cualquier valor de peso entre el mínimo y máximo de una distribución). Las discretas son las que solo pueden adoptar ciertos valores dentro de un conjunto como, por ejemplo, el número de hijos o el número de episodios de isquemia coronaria.
Por otra parte están las variables cualitativas, que representan atributos o categorías de la variable. Cuando las variable no incluye ningún sentido de orden, se dice que es cualitativa nominal, mientras que si se puede establecer cierto orden entre las categorías diríamos que es cualitativa ordinal. Por ejemplo, la variable fumador sería cualitativa nominal si tiene dos posibilidades: sí o no. Sin embargo, si la definimos como ocasional, poco fumador, moderado o muy fumador, ya existe cierta jerarquía y hablamos de variable cualitativa ordinal.
Diagrama de barras
Pues bien, el diagrama de barras sirve para representar las variables cualitativas ordinales. En el eje horizontal se representan las diferentes categorías y sobre él se levantan unas columnas o barras cuya altura es proporcional a la frecuencia de cada categoría. También podríamos utilizar este tipo de gráfico para representar variables cuantitativas discretas, pero lo que no es correcto hacer es usarlo para las variables cualitativas nominales.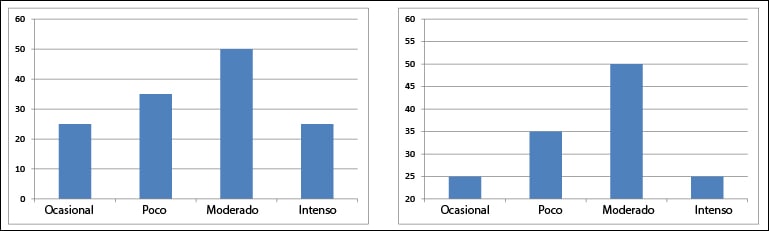
El gran mérito de los diagramas de barras es expresar la magnitud de las diferencias entre las categorías de la variable. Pero ahí está precisamente, su punto débil, ya que son fácilmente manipulables si modificamos los ejes. Como podéis ver en la primera figura, la diferencia entre poco y fumadores ocasionales parece mucho mayor en el segundo gráfico, en el que nos hemos comido parte del eje vertical. Por eso hay que tener cuidado al analizar este tipo de gráficos para evitar que nos engañen con el mensaje que el autor del estudio pueda querer transmitir.
Histograma
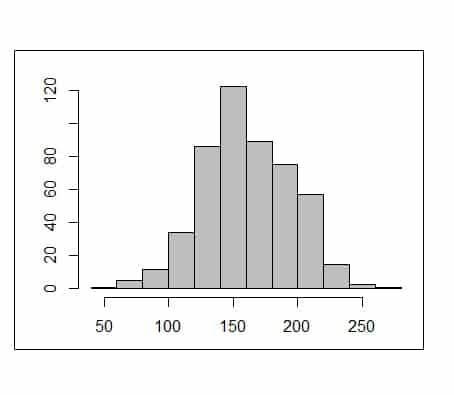
Como veis en la segunda figura, las columnas, a diferencia del diagrama de barras, están todas juntas y el punto medio es el que da el nombre al intervalo. Los intervalos no tienen por qué ser todos iguales (aunque es lo más habitual), pero siempre tendrán un área mayor aquellos intervalos con mayor frecuencia.
Existe, además, otra diferencia muy importante entre el diagrama de barras y el histograma. En el primero solo se representan los valores de las variables que hemos observado al hacer el estudio. Sin embargo, el histograma va mucho más allá, ya que representa todos los valores posibles que existen dentro de los intervalos, aunque no hayamos observado ninguno de forma directa.
Permite así calcular la probabilidad de que se represente cualquier valor de la distribución, lo que es de gran importancia si queremos hacer inferencia y estimar valores de la población a partir de los resultados de nuestra muestra.
Nos vamos…
Y aquí dejamos estos gráficos que pueden parecer lo mismo pero que, como queda demostrado, se parecen como un huevo a una castaña.
Solo un último comentario. Dijimos al principio que era un error utilizar diagramas de barras (y no digamos ya histogramas) para representar variables cualitativas nominales. ¿Y cuál utilizamos?. Pues un diagrama de sectores, la famosa y ubicua tarta que se utiliza en más ocasiones de las debidas y que tiene su propia idiosincrasia. Pero esa es otra historia…

Que fácil lo haces todo, Manuel! Me encanta la claridad con la que sabes exponer temas tan áridos como este que dominas.
Muchísimas gracias por compartirlo.
Excelente idea explicar aspectos que habitualmente uno no se plantea pero que aparecen con gran frecuencia en los estudios.