Signs test.

Signs test compares two medians using the direction of the values with respect to the mean and binomial probability.
In the world of science in general and of medicine in particular, we are used to doing everything in a very precise and detailed way. Who has not ever ordered Amoxicillin 123.5 mg every eight hours to a patient?. However, things can be done in a rougher although not botched way. Of course, ir must be done according to certain rules. Let’s see an example.
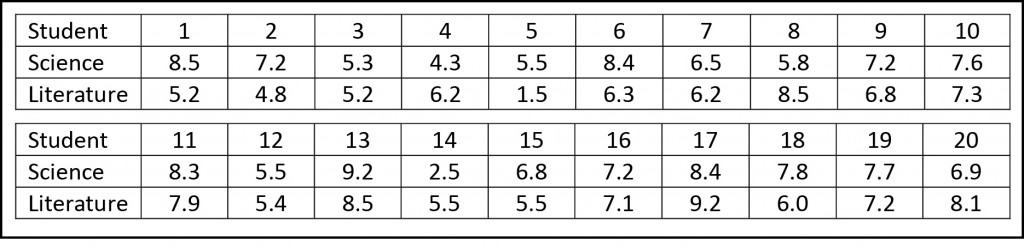
Suppose we want to know if our education system is as good as it should be. Consider that we select a class of twenty students in the first year of high school and that we make them to take two easy examinations, one on natural history and another one on literature. You can see their results in the attached table.
If you take the time to calculate it, students obtain an average score of 6.8 points in science, with a standard deviation (SD) of 1.6. Meanwhile, their literature’s scores have an average mark of 6.4 with a SD of 1.7. It seems, then, that our students are better prepared for sciences than for literature. The immediate question is: can we extrapolate this results to all students in our educational system?.
Let’s calculate
If we want to know it, we just have to do a Student’s t test, assuming that distribution of scores fits a normal curve, which seems reasonable to me. We could use a statistical software or do it by ourselves, calculating the mean’s difference and the standard error of the difference to get the value of t and its probability, so that we can find out if we can reject or accept the null hypothesis, which in this case is that the observed difference is due to chance and that the knowledge of our guys are similar in both subjects.
But we said we were going to do it in a rougher and much simpler way. If you review the results, most of the students (fifteen) have higher scores in science, while only five (numbers 4, 8, 14, 17 and 20) have a better mark in literature. Let’s think about it a little.
If the null hypothesis that knowledge on the two subjects are similar were true, the probability of having a better mark in any of the two subjects would be 50% (0.5). It means that ten students should have better marks in science and ten in literature. So we ask: what is the probability that the observed difference (fifteen instead of ten) is due to chance?.
And this, ladies and gentlemen , is a typical case of binomial probability, where n=20, p=0.5 and k>14 (being n the number of students, p the probability of having a better mark in science, and k the number of students with a higher science score). We can solve the problem using the binomial probability equation or using one of the available calculators on the Internet. In any case, we’ll reach the conclusion that the probability of coming up with fifteen higher scores in science by chance is 2.07%. Therefore, as it’s less than 5%, we’ll reject our null hypothesis and will conclude that our students are more gifted for science, always, of course, with a 5% probability of committing a type 1 error.
Signs test
This test that we have done have the beautiful name of signs test, and it’s one of the many non-parametric tests that can be used for statistical inference. As we have seen, it doesn’t take into account either the value of the parameters (for some reason it’s called non-parametric) or the magnitude of the differences, neither it requires that the data follow a normal distribution or a very large sample size.
This is why non-parametric tests are often used when normality cannot be assumed or when the sample size is small, but we could use them in any situation. Why are they not always used? Well, mainly because they are more stringent than parametric tests and require a greater magnitude of effect in order to reject the null hypothesis.
We’re leaving…
And with that we end this post. Do not think that all non-parametric tests are so simple. Here we have talked about a simple way to compare two means (actually, two medians), but there are also ways to compare more than two, such as the Kruskal-Wallis test. But that’s another story…