Survival tables and censored data.

We describe the methodology of preparing survival tables and the treatment of censored data in this type of study with time to event variables.
In the best-known sense, censorship is the action of examining a work intended for the public, suppressing or modifying the part that does not fit certain political, moral or religious aspect, to determine whether or not it can be published or exhibited. So what do we mean in statistics when we talk about censored data? Nothing to do with politics, morality or religion. In order to explain what a censored data is, we must first discuss the time-to-event variables and survival analyzes.
In general, we can say that there are three types of variables: quantitative, qualitative and time-to-event. The first two are fairly well understood in general, but the time-to-event are a little more complicated to understand.
Time-to-event variables
Imagine that we want to study the mortality of that terrible disease that fildulastrosis is. We could count the number of deaths at the end of the study period and divide them by the total population at the beginning. For example, if at the beginning there are 50 patients and four die during follow-up, we could calculate the mortality as 4/50 = 0.08, or 8%. Thus, if we have followed the population for five years, we can say that the survival of the disease at five years is 92% (100-8 = 92).
Simple, isn’t it? The problem is that this is only valid when all subjects have the same follow-up period and no losses or dropouts occur throughout the study, a situation that is often far from the reality in most cases.
In these cases, the correct thing to do is to measure not only if death occurs (which would be a dichotomous variable), but also when it occurs, also taking into account the different follow-up period and the losses. Thus, we would use a time-to-event variable, which is composed of a dichotomous variable (the event being measured) and a continuous variable (the follow-up time when it occurs).
Following the example above, participants in the study could be classified into three types: those who die during follow-up, those who remain alive at the end of the study, and those who are lost during follow-up.
Of those who die we can calculate their survival but, what is the survival of those who are alive at the end of the study? And what is the survival of those who are lost during follow-up? It is clear that some of the lost may have died at the end of the study without us detecting it, so our measure of mortality will not be accurate.
Survival tables and censored data
And this is where we find the censored data. All those who do not present the event during the survival study are called censored (losses and those who finish the study without presenting the event). The importance of these censored data is that they must be taken into account when doing the survival study, as we will see below.
The methodology to be followed is to create a survival table that takes into account the events (in this case the deaths) and the censored data, as we can see in the attached table.
The columns of the table represent the following: x, the year number of the follow-up; Nx, the number of participants alive at the beginning of that year; Cx, the number of losses of that year (censored); Mx, the number of deaths during that period; PD, probability of dying in that period; PPS, the probability of surviving in that period (the probability of not presenting the event); And PGS, the global probability of survival up to that point.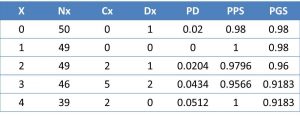
As we see, the first year we started with 50 participants, one of whom died. The probability of dying in that period is 1/50 = 0.02, so the probability of survival in the period (which is equal to the global since it is the first period) is 1-0.02 = 0, 98.
In the second period we start with 49 and no one dies or is lost. The PD in the period is zero and survival one. Thus, the overall probability will be 1×0.98 = 0.98.
In the third period we continue with 49. Two are lost and one dies. The PD is 1/49 = 0.0204 and the PPS is 1-0.0204 = 0.9796. If we multiply the PSP by the global of the previous period, we obtain the overall survival of this period: 0.9796×0.98 = 0.96.
In the fourth period we started with 46 participants, resulting in five losses and two deaths. The PD will be 2/46 = 0.0434, the PPS of 1-0.0434 = 0.9566 and the PGS of 0.9566×0.96 = 0.9183.
And last, in the fifth period we started with 39 participants. We have two censored and no event (death). PD is zero, PPS is equal to one (no one dies in this period) and PGS 1×0.9183 = 0.9183.
Finally, taking into account the censored data, we can say that the overall survival at five years of fildulastrosis is 91.83%.
We’re leaving…
And with this we are going to leave it for today. We have seen how a survival table with censored data is constructed to take into account unequal follow-up of participants and losses during follow-up.
Only two thoughts before finishing. First, even if we talk about survival analysis, the event does not have to be the death of the participants. It can be any event that occurs throughout the study follow-up.
Second, the time-to-event and censored data are the basis for performing other statistical techniques that estimate the probability of occurrence of the event under study at a given time, such as the Cox regression models. But that is another story…
