Theoretical quantiles graph.

The theoretical quantiles graph (q-q plot), used to check the normality of the data of a distribution, is reviewed.

It’s often said that comparisons are odious. And the truth is that it is not appropriate to compare people or things together, since each has its values and there’s no need of being slighted for doing something differently. So it’s not surprising that even the Quixote said that comparisons are always odious.

Of course, this may be said about everyday life, because in medicine we are always comparing things together, sometimes in a rather beneficial way.

Today we are going to talk about how to compare two data distributions graphically and we’ll look at an application of this type of comparison that helps us to check whether our data follow a normal distribution.

Graphics methods to assess normality

Imagine for a moment that we have a hundred serum cholesterol values from schoolchildren. What will we get if we plot the value against themselves linearly? Simple: the result would be a perfect straight line cross the diagonal of the graph.

Now think about what would happen if instead of comparing with themselves we compare them with a different distribution. If the two data distributions are very similar, the dots on the graph will be placed very close to the diagonal. If the distributions differ, the dots will go away from the diagonal, the further the more different the two distributions. Let’s look at an example.

Let’s suppose we divide our distribution into two parts, the cholesterol of boys and girls. According to what our imagination tells us, the boys eat more industrial bakery than the girls, so their cholesterol level are higher, as you can see if you compare the curve from girls (black) with those of children (blue). Now, if we represent the values of the girls against the values of the boys linearly, as can be seen in the figure, the dot are far from the diagonal, being evenly over it. What is the reason of this? The values of boys are higher than the values of girls.

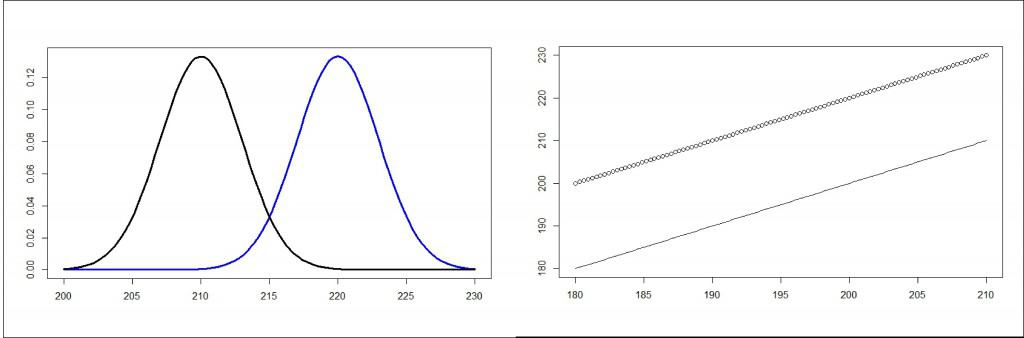
You will tell me that all this is fine, but it can be a bit unnecessary. After all, if we want to know who have the highest values all that we have to do is look at the curves. And you will be right in your reasoning, but this type of graph has been designed for something different, which is to compare a distribution with its normal equivalent.

Theoretical quantiles graph (q-q plot)

Imagine that we have our first global distribution and we want to know if it follows a normal distribution. We only have to calculate its mean and standard deviation and represent its quantiles against the theoretical quantiles of a normal distribution with the same mean and standard deviation. If our data are normally distributed, the dots will align with the diagonal of the graph. The more they go away from it, the less likely that our data follow a normal distribution. This type of graph is called quantile-quantile plot or, more commonly, q-q plot.

Let’s see an example of q-q plot for its better understanding. In the second graph you can see two curves, one blue colored representing a normal distribution and a black one following a Student’s t distribution. On the right side you can see the q-q plot of the Student’s distribution. Central data fits quite well the diagonal, but extreme data do it worse, varying the slope of the line. This indicates that there are more data under the tails of the distribution that the data that there would be if it were a normal distribution. Of course, this should not surprise us, since we know that the “heavy tails” are a feature of the Student’s distribution.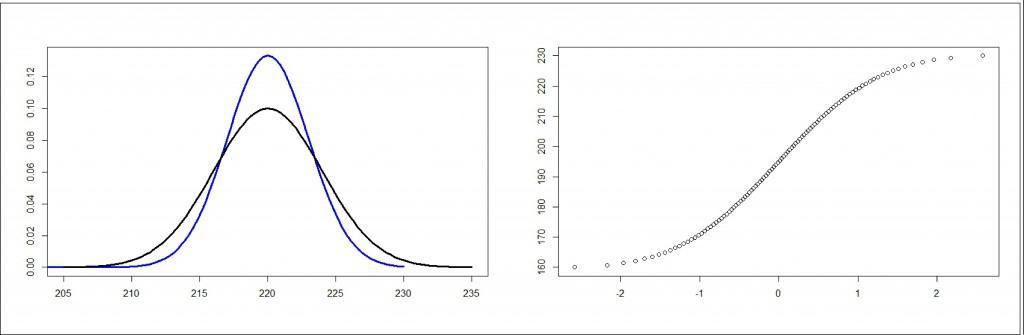

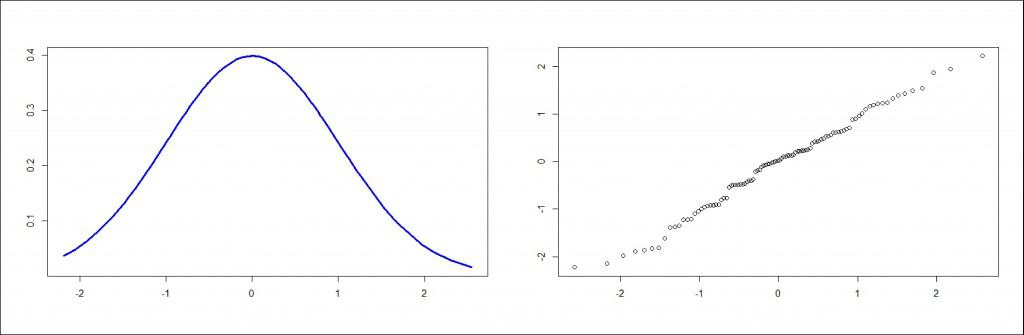
Finally, in the third graph you can see a normal distribution and its q-q plot, in which we can see how the dots fit quite well to the diagonal of the graph.

As you can see, the q-q plot is a simple graphical method to determine if the data follow a normal distribution. You may say that it would be a bit tedious to calculate the quantiles of our distribution and those of the equivalent normal distribution, but remember that most statistical software can do it effortlessly. For instance, R has a function called qqnorm() that draws a q-q plot in a blink.

We’re leaving…

And here we are going to end with the normal fitting by now. Just remember that there’re other more accurate numerical methods to find out if data fit a normal distribution, such as the Kolmogorov-Smirnov’s test or the Shapiro-Wilk’s test. But that’s another story…