Probabilidad y regresión lineal.

En 1665, el físico Christiaan Huygens, inventor del reloj de péndulo, se encontraba en cama, convaleciente de una enfermedad, mirando cómo dos relojes de péndulo colgados de la misma viga tendían a oscilar en sincronía, fenómeno que él describió como una «extraña simpatía».

Al principio, el fenómeno parecía un simple capricho de la mecánica. Durante mucho tiempo se aceptó como una curiosidad sin preguntarse demasiado por qué ocurría. Pero Huygens, intrigado, descubrió que la causa estaba en las vibraciones casi imperceptibles que los péndulos transmitían a través de su soporte común.

Lo que parecía una coincidencia era, en realidad, el resultado inevitable de una conexión física sutil.

Y os cuento esta historia porque algo parecido pasa con la famosa práctica de minimizar la suma de los errores al cuadrado en la regresión lineal. Muchos manuales justifican esta elección de los mínimos cuadrados diciendo que así evitamos que los errores positivos se anulen con los negativos. Para evitar esto también podrían sumarse los valores absolutos de los errores, llamados residuos, pero lo cuadrados tienen la ventaja de que penalizan más los errores mayores que los más pequeños.

Y esta es la razón que os contarán los libros de estadística para elegir la suma de cuadrados. Y no es mentira, pero hay una razón mucho más profunda.

Al igual que pasaba con los péndulos de Huygens, aceptar esas explicaciones sin profundizar, nos deja a mitad de camino. ¿Por qué usar los cuadrados y no alguna otra fórmula razonable, como el cubo u otra potencia más alta?

La clave está, esta vez, en una necesidad oculta: si asumimos que los residuos son aleatorios y siguen una distribución normal, minimizar los cuadrados no será una simple preferencia práctica, sino consecuencia obligada de esa hipótesis probabilística. Hoy vamos a ver cómo, detrás de decisiones que parecen cómodas o convenientes, a veces se esconden principios fundamentales que nos obligan, suavemente, pero sin escapatoria, a seguir ciertos caminos.

Una visión probabilística de la regresión lineal

Ya hemos visto cómo la explicación tradicional de la regresión lineal suele empezar con una especie de acto de fe: el mejor modelo es aquel que minimiza la suma de las distancias al cuadrado entre los puntos observados y la recta de regresión (o, lo que es lo mismo, la predicción del modelo para esos puntos). Estas distancias son los errores o residuos.

Y aunque las razones para minimizar los cuadrados parecen adecuadas, el fondo del asunto es un poco más complejo y, para llegar a él, emplearemos un enfoque probabilístico de la regresión lineal que nos dará otra forma de mirar el problema, mucho más rica y reveladora.

Como ya sabemos, el objetivo de la regresión lineal es predecir el valor de una variable dependiente continua en función de la suma ponderada de los valores de una serie de variables independientes. Esta ponderación se hace mediante los llamados coeficientes de regresión, según la fórmula que os muestro a continuación:

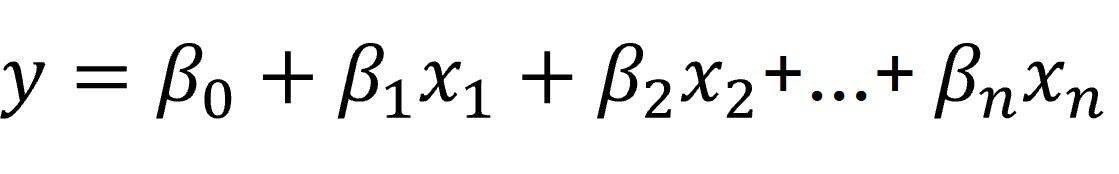
La regresión lineal consiste, entonces, en averiguar qué conjunto de coeficientes (B) hace que nuestro modelo explique los datos lo mejor posible.

El problema con el que nos enfrentamos es que el modelo lineal subyacente a esta ecuación no es perfecto y siempre habrá diferencias entre los valores predichos por el modelo y los valores reales observados. Las predicciones estarán corrompidas por una especie de ruido, que vendrá de múltiples factores existentes en la vida real. Este ruido es todo lo que no podemos explicar con el modelo, pero que debemos incluir en su definición:

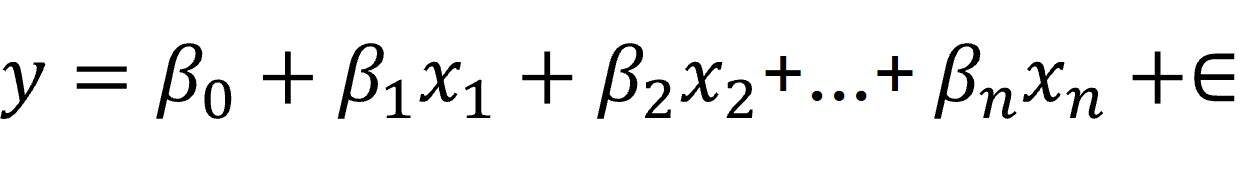
Así, debemos reescribir la frase que enunciamos un poco más arriba: la regresión lineal consiste, entonces, en averiguar qué conjunto de coeficientes (B) hace que nuestro modelo explique los datos lo mejor posible… teniendo en cuenta ese ruido, los residuos del modelo.

Y la clave está en que la ecuación de regresión que obtengamos dependerá de las suposiciones que hagamos sobre estos residuos.

Una suposición muy normal

Ya entendemos cómo la naturaleza de los residuos es clave para el cálculo de los coeficientes de regresión.

También sabemos que estos errores pueden deberse a errores de medición, variables que no estamos considerando, o incluso simples caprichos del azar. En cualquier caso, los residuos están formados por la suma de muchas pequeñas influencias independientes que se añaden.

Y aquí es donde entra en acción uno de los pilares de la estadística. Según el teorema del límite central, cuando agrupemos todas estas variables aleatorias, la suma resultante se aproximará a una distribución normal.

Así que, siguiendo las indicaciones de este teorema, parece conveniente asumir que los residuos siguen una distribución normal.

En busca de la verosimilitud

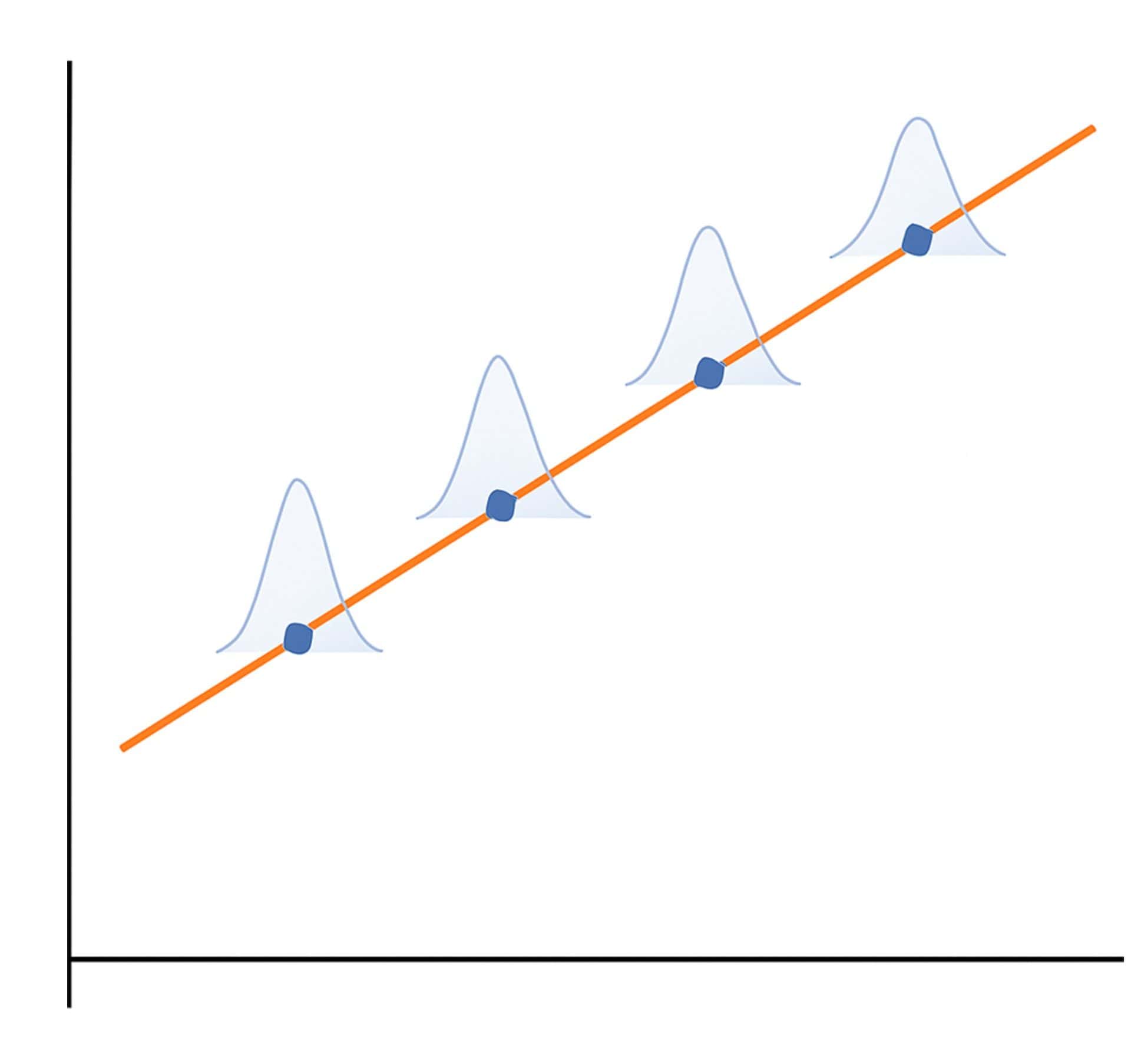
Ahora que hemos asumido que los residuos siguen una distribución normal, cuando observamos un determinado punto de la recta, podemos estimar cuánto ruido puede agregarse a nuestra hipótesis del modelo ideal. Alrededor del punto estimado por el modelo, hay una zona de incertidumbre en forma de campana centrada en el punto ideal, tal como veis en la figura adjunta. Esta zona representa la cantidad de error que puede cometer el modelo y su probabilidad.

Para que parezca que sabemos de qué estamos hablando, vamos a poner un poco de notación matemática. Esta probabilidad puede expresarse de la siguiente manera:

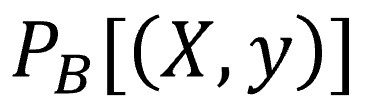
En esta notación, B representa el conjunto de los coeficientes del modelo, X representa un determinado conjunto de valores de las variables independientes (por eso está en mayúscula, porque, en realidad, es una matriz de variables) e “y” representa el valor de la variable dependiente (que es solo una variable, por eso está en minúscula).

Esta probabilidad, que sigue una distribución normal y está centrada en el punto, tendrá una amplitud que dependerá del valor de los coeficientes de regresión. Así, para un mismo conjunto de coeficientes B, podemos calcular la probabilidad de obtener una determinada cantidad de error utilizando la fórmula de la distribución normal, que nos vamos a ahorrar, por ahora.

Si vamos un paso más allá, bajo el supuesto de que todos los puntos se muestrearon de forma independiente, la probabilidad de obtener nuestro conjunto de datos completos puede expresarse como el producto de las probabilidades individuales de cada punto.

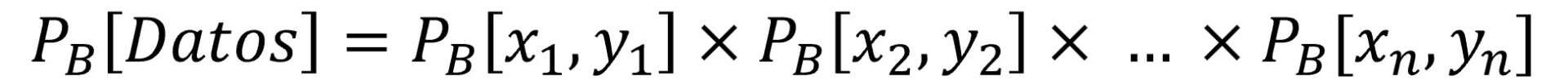
Esta probabilidad de obtener nuestro conjunto de datos para un determinado conjunto de coeficientes de regresión es lo que llamamos la verosimilitud del modelo. Si tenemos varios modelos con sus distintos coeficientes, será mejor modelo aquel que tenga mayor verosimilitud o, lo que es lo mismo, una mayor probabilidad de obtener los datos actuales con sus coeficientes específicos.

Y fijaos un momento que hemos hecho un cambio de punto de vista importante. El objetivo a la hora de elaborar el modelo ya no es minimizar los errores, sino maximizar la verosimilitud: encontrar los coeficientes que hacen más probable que el modelo genere los datos que hemos observado. Pongamos otra formulita para celebrarlo debidamente:

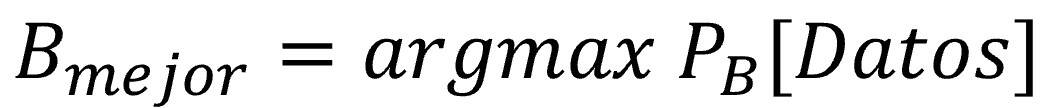
Para completar el panorama, en la fórmula anterior podemos expresar la probabilidad de los datos como el producto de las probabilidades independientes de cada uno de los puntos:

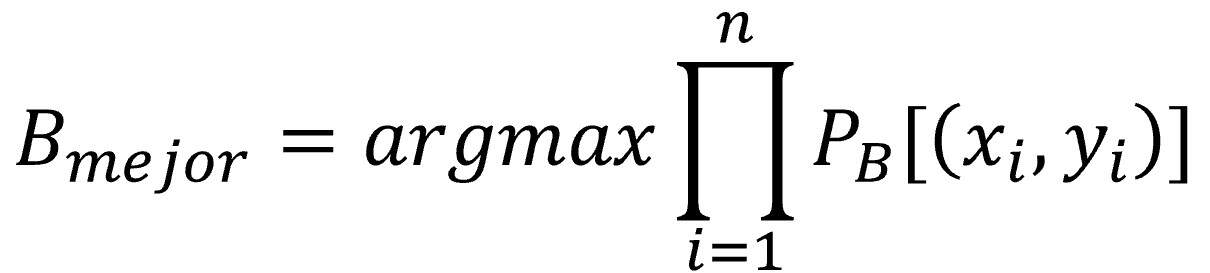
Todos los caminos conducen a Roma

Ya estamos en la recta final de esta carrera, así que nos vamos a permitir complicar un poco (no mucho) la notación matemática para acabar de completar lo que queremos demostrar. Ya sabéis, una imagen vale más que mil palabras (o eso dicen).

Como la fórmula anterior parece un poco antipática y difícil de manejar, vamos a simplificarla, aunque parezca mentira, aplicando logaritmos a su parte derecha.

La gran ventaja de aplicar los logaritmos es que el logaritmo de un producto es igual a la suma de logaritmos y nos va a resultar más fácil manejar la suma que el producto. La ecuación nos queda así:

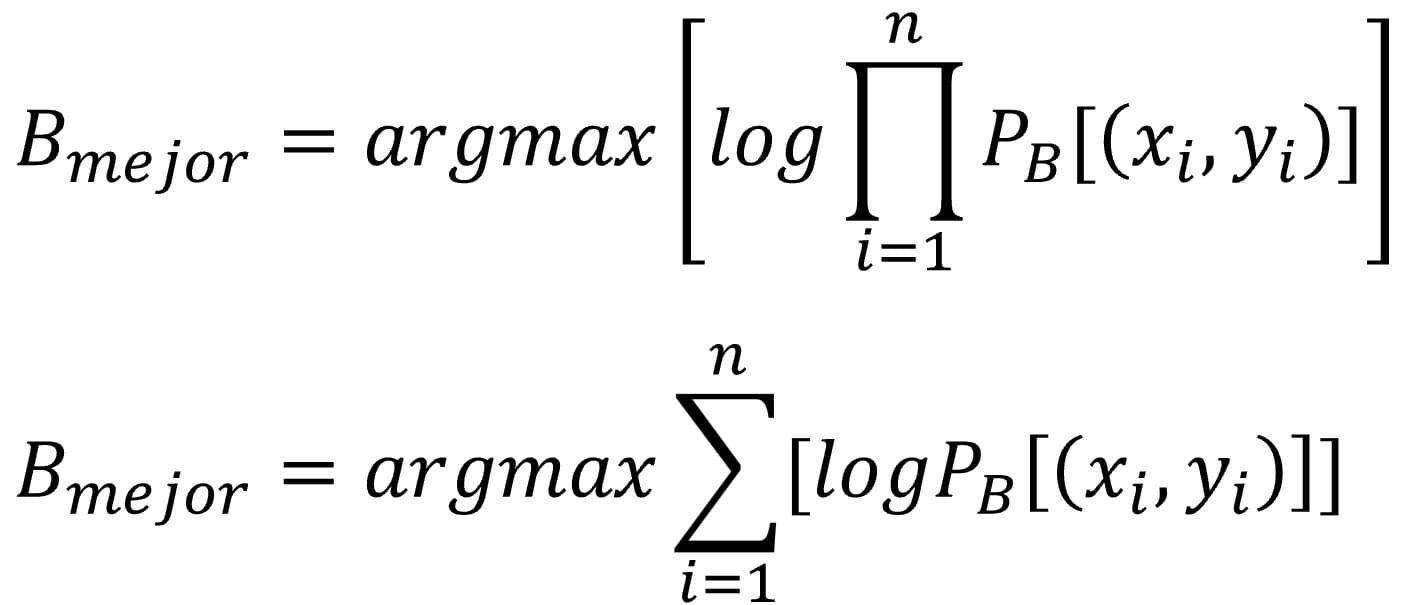
Y ahora, que nadie desespere, vamos a sustituir la verosimilitud por su valor según la ecuación de la distribución normal, tal como veis a continuación:

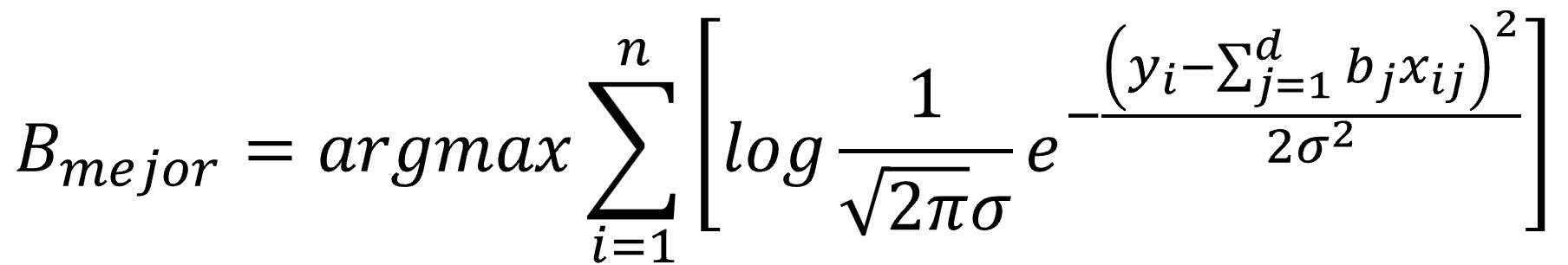
Por favor, que nadie se vaya todavía. A estas alturas, alguno pensará que he puesto la fórmula anterior en un acto de puro sadismo, pero nada más lejos de la realidad.

Lo primero, aclarar que el término “d” de la ecuación representa el número de variables independientes del modelo. Ahora vamos a fijarnos en el resto de los componentes de la fórmula.

Aparte de nuestros datos y nuestros coeficientes, todos los componentes de la ecuación normal son constantes, salvo la desviación estándar, sigma. Pero resulta que sigma no influye sobre el conjunto de coeficientes que maximicen la verosimilitud del modelo, ya que es un valor fijo que no influye desde el punto de vista de la optimización del modelo.

En resumen, podemos simplificar la ecuación quitando sigma y las constantes (que no influyen en el procedimiento de optimización), además del logaritmo, que se anula con la exponencial (todo lo que está elevado al número e). Mirad con atención lo que obtenemos:

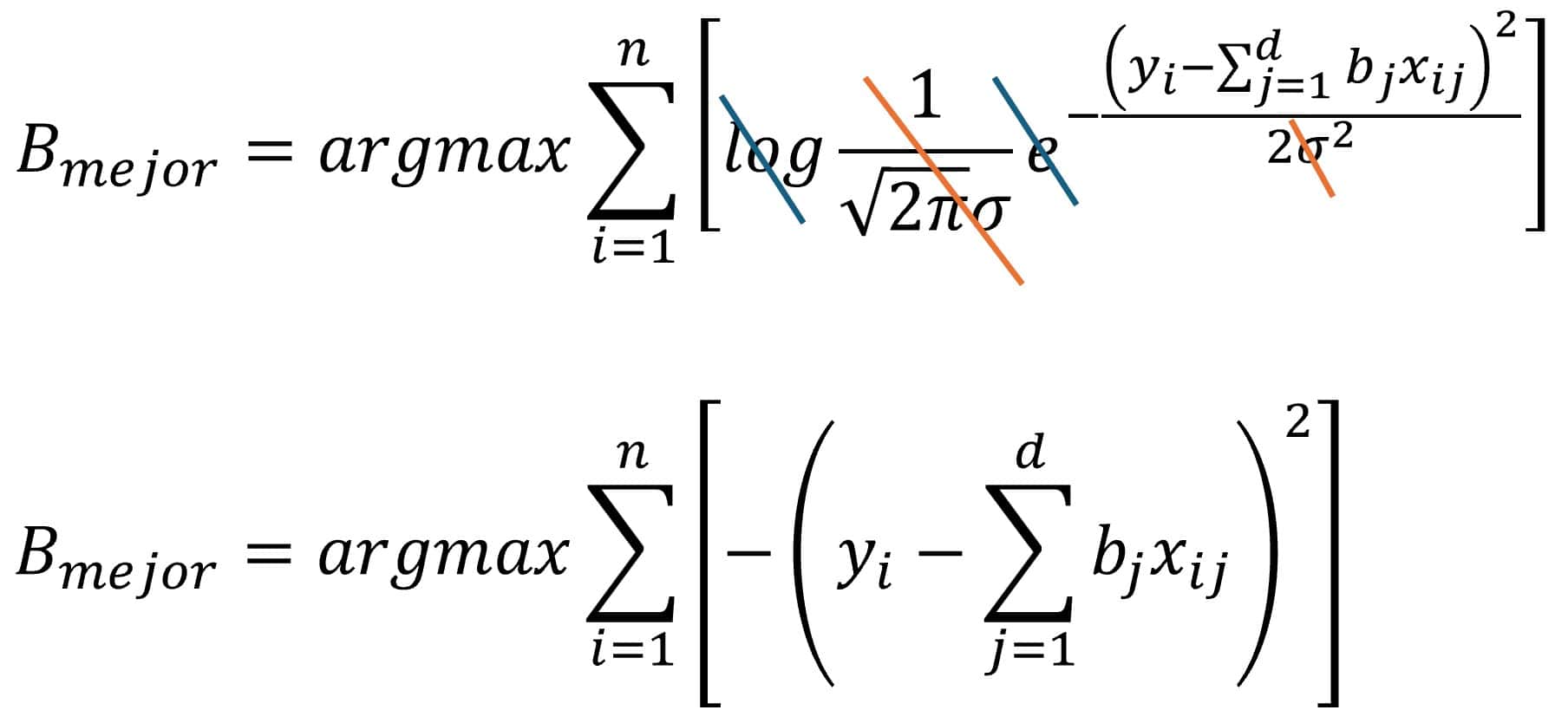
Según esta fórmula, los coeficientes óptimos deben maximizar el negativo de la suma de los cuadrados de los errores entre el ajuste lineal y los puntos observados, o sea, la suma del cuadrado de los residuos.

Para iluminar este punto, que ahora parece oscuro, vamos a hacer una última transformación a la ecuación para manejar los valores positivos de los errores que, lógicamente, querremos minimizar (pensadlo, maximizar el negativo del valor o minimizar el positivo del mismo valor viene a ser la misma cosa):

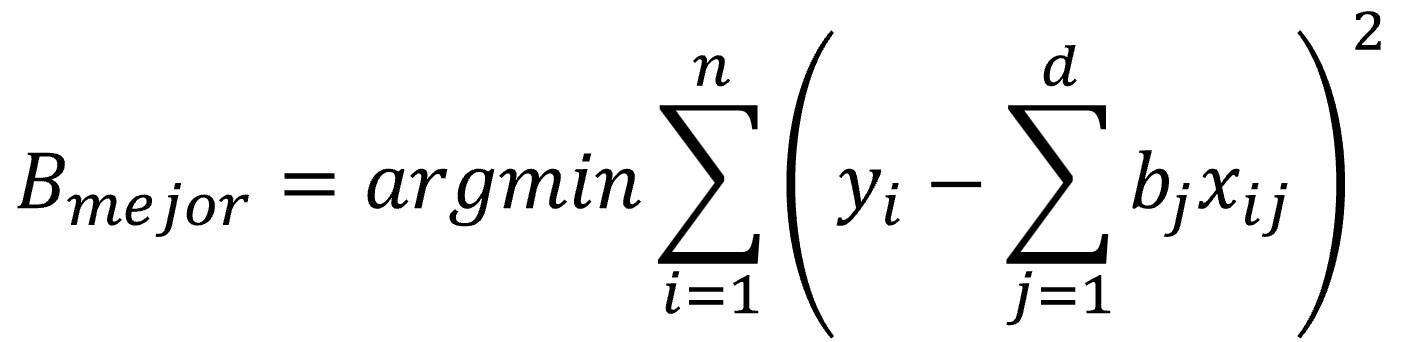
Una vez más, todos los caminos conducen a Roma. Si partimos de la hipótesis de que los residuos siguen una distribución normal y eliminamos todo aquello que no influye en la optimización del modelo, lo que aparece como por arte de magia es… ¡la famosa fórmula de los mínimos cuadrados!

Para decirlo de una forma mucho más elegante, hemos visto que maximizar la log-probabilidad o verosimilitud es equivalente a minimizar la suma de los cuadrados de los residuos.

Nos vamos…

Y aquí me despido, por hoy, de los que aun sigáis leyendo esta entrada, suponiendo que quede alguien.

Hemos visto que no elevamos los residuos al cuadrado porque sea más fácil o más justo. Lo hacemos porque es lo que hay que hacer si creemos que los residuos siguen una distribución normal, lo que no deja de ser un supuesto que debe cumplirse para poder aplicar la regresión lineal.

Minimizar la suma de los cuadrados es maximizar la verosimilitud bajo esa suposición. Y por eso, aunque parezca una costumbre sin sentido, hay toda una lógica matemática marcando el paso de este baile. El cuadrado es una consecuencia directa de suponer que los errores son normales.

Como los péndulos de Huygens, que parecían coordinarse por pura cortesía mecánica, nuestros modelos estadísticos también entran en sintonía… pero con la campana de Gauss. Cuando todo vibra a la misma frecuencia, ocurre algo casi mágico: el modelo no solo funciona, sino que, en ocasiones, hasta tiene sentido. Y si pensabais que esto era lo más elegante que podía ofrecer la regresión lineal, esperad a ver qué ocurre cuando empecemos a penalizar a los modelos demasiado entusiastas. Porque sí, la elección de los términos de regularización (como ridge o lasso) también tiene su explicación probabilística, añadiendo nuestra suposición previa de cómo debería funcionar el modelo, al más puro estilo bayesiano. Pero esa es otra historia…