Regresión logística multinomial.

En los años 60 del siglo pasado, la NASA tenía un problema. Bueno, varios, pero uno particularmente molesto: ¿cómo decidir si un astronauta estaba lo suficientemente sano como para ir a la Luna? No podían arriesgarse a enviar a alguien con una enfermedad oculta, pero tampoco podían descartar a candidatos solo por precaución. Así que diseñaron un protocolo de evaluación médica con pruebas y criterios específicos: cada astronauta se clasificaba como “apto” o “no apto” para la misión.

Todo bien… hasta que se dieron cuenta de que el problema no terminaba ahí. No solo había que decidir quién volaba, sino también qué rol se le adjudicaba: comandante, piloto o especialista de misión. Y entonces quedó claro que, a veces, más de dos no son multitud, sino la oportunidad de una clasificación mejor.

La vida está llena de decisiones que no se reducen a un simple “sí o no”. Diagnosticar una infección, clasificar imágenes o incluso recomendar películas, no es tan simple como dividir el mundo en dos categorías. Necesitamos herramientas que nos permitan distribuir probabilidades entre múltiples opciones sin perder precisión.

La regresión logística binaria nos ayuda a tomar decisiones entre dos opciones, pero cuando el problema se complica y hay más categorías en juego, necesitamos una versión más poderosa.

Es aquí donde la regresión logística multinomial entra en escena: una evolución natural de la regresión logística binaria que nos permite manejar situaciones donde hay más de dos posibles respuestas.

Seguid leyendo y veréis cómo dar el salto más allá de lo binario.

La doble opción de lo binario

La base de la que vamos a partir es la regresión logística binaria, que vamos a ilustrar sirviéndonos del programa R y de un conjunto de datos totalmente inventado sobre la marcha. Los más atrevidos podéis acceder al código de R que utilizaremos en esta entrada haciendo clic en este enlace.

Volviendo al problema inicial de la NASA, vamos a suponer que nuestros ingenieros tienen los registros de 20 astronautas, de los que han recogido dos variables. Una variable cuantitativa que es la puntuación de una prueba de desempeño físico, a la que llamaremos test_score, y una variable binaria codificada como 1, cuando el astronauta fue considerado “apto” para el vuelo, y 0, cuando fue considerado “no apto”. A esta variable la podemos llamar aptitude, como harían nuestros americanos ingenieros. Los datos son los siguientes:

test_score: 3.1, 2.5, 2.7, 5.7, 2.5, 3.7, 1.8, 3.1, 4.0, 3.0, 5.0, 4.2, 2.2, 4.1, 4.3, 1.3, 5.1, 2.1, 2.8 y 2.7.

aptitude: 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1.

Ahora queremos construir un modelo que nos permita predecir, para futuros candidatos al programa espacial, la probabilidad de que sean o no “aptos” para el mismo. Como la variable diana es binaria (0 / 1), no podemos utilizar la regresión lineal, pensada para predecir valores continuos y cuya predicción puede ser cualquier número real, cuando necesitamos que se acote al intervalo [0, 1], el de los valores posibles de probabilidad.

Para garantizar que la predicción del modelo esté entre 0 y 1, transformamos la salida de la regresión lineal aplicando la función logística o sigmoide, que toma la siguiente forma:

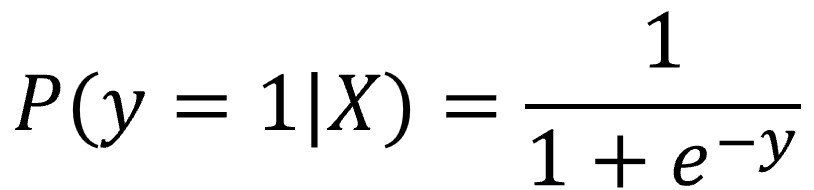
Así, sustituyendo el valor de “y” según la ecuación de la regresión lineal, podemos calcular la probabilidad de que la variable dependiente valga 1 de la siguiente manera:

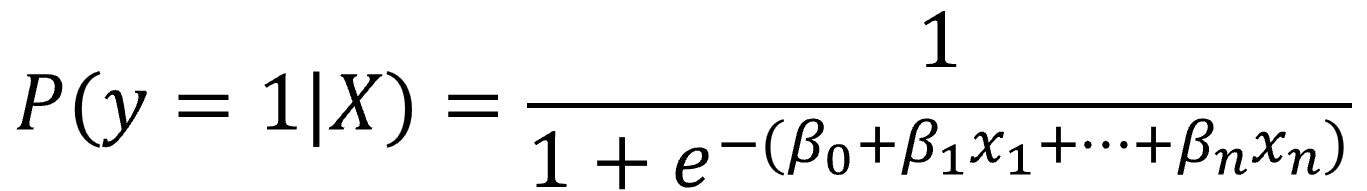
En la regresión logística, en lugar de modelar directamente P(y = 1), modelamos el logaritmo del cociente de probabilidades (odds), obteniendo la ecuación final del modelo:

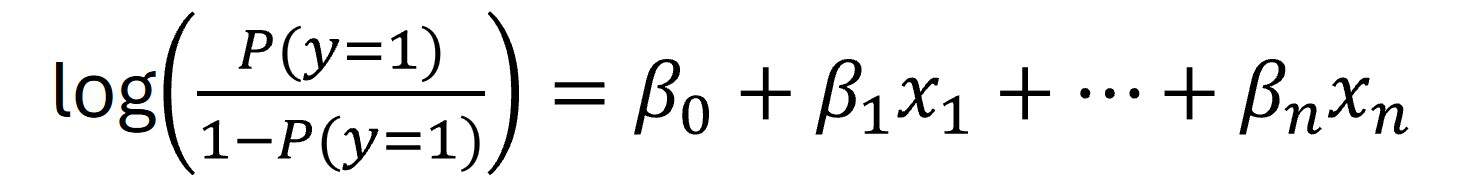
Una vez aclarado todo esto, nos vamos a R, introducimos el comando adecuado y obtenemos el siguiente modelo:

aptitude = -6,7 + 2,1 x test_score

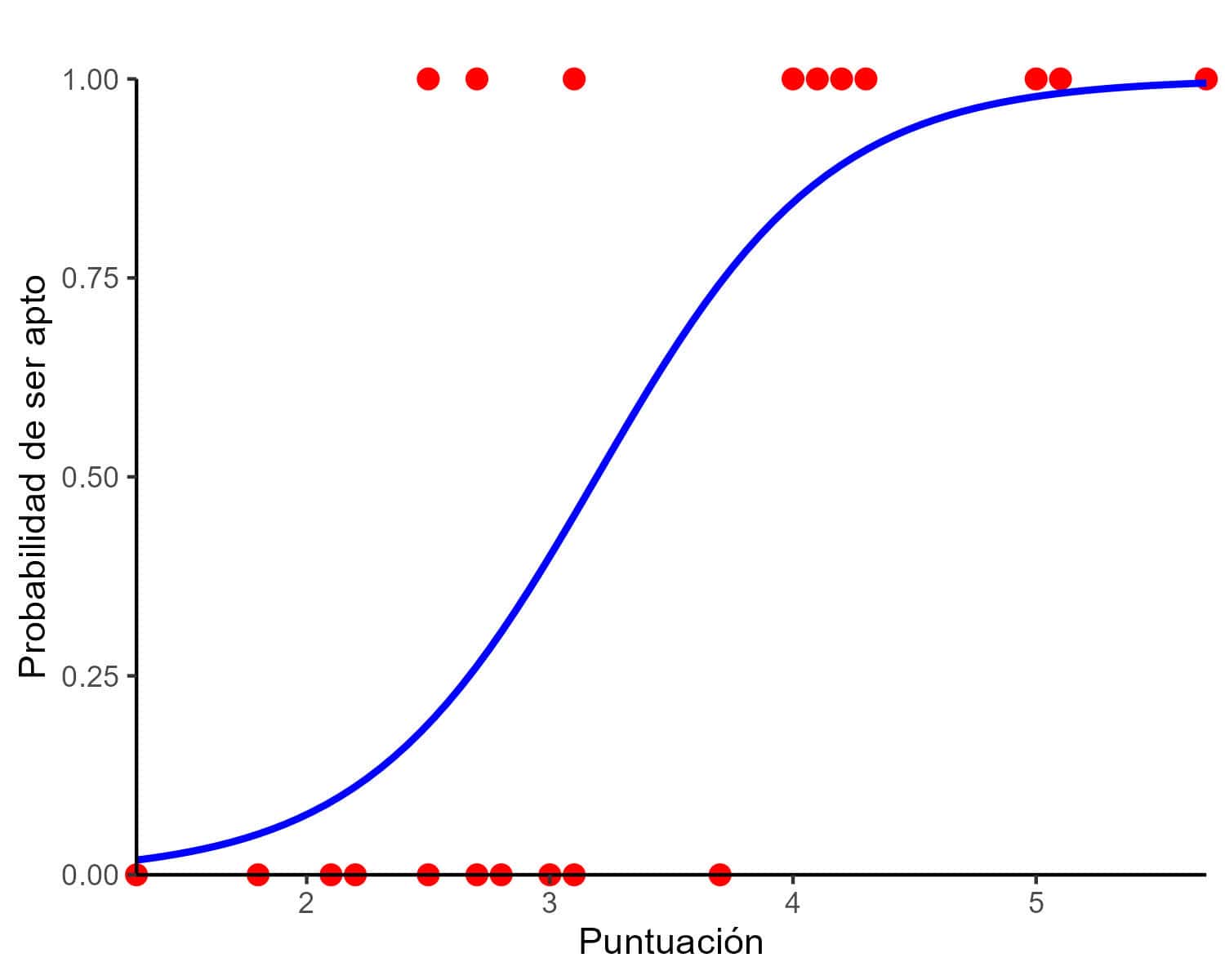
Podemos ver una representación del modelo en la figura adjunta. Con esta figura, podríamos aproximar cuál sería la probabilidad de ser “apto” de un nuevo candidato que tuviese una puntuación de, digamos, 3,5: un poco por encima del 50%.

Pero podemos obtener una estimación más precisa, introduciendo la puntuación en la ecuación del modelo y utilizando la función sigmoide para calcular la probabilidad:

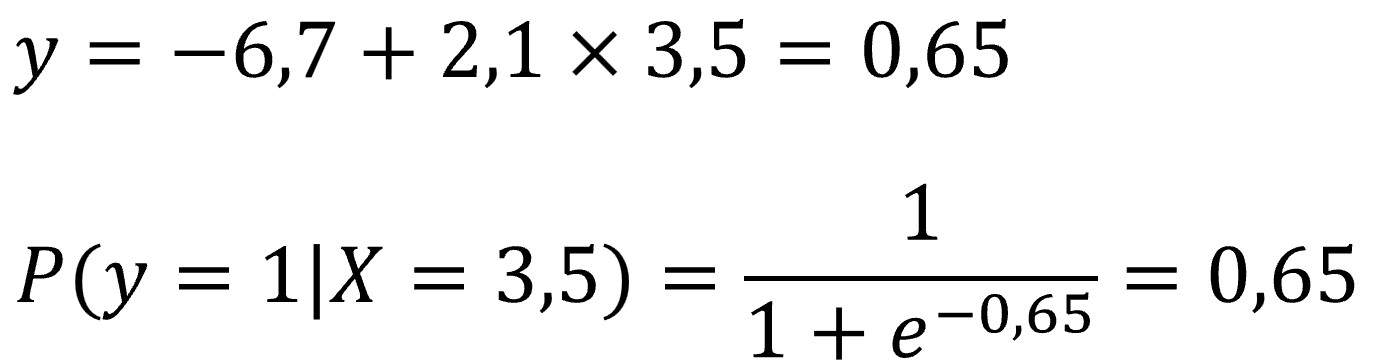
Ya sabemos que un candidato con una puntuación de 3,5 tendrá una probabilidad del 65% de ser “apto” para el programa espacial.

Cuando lo binario no es suficiente

Nuestros chicos de la NASA ya saben cómo predecir qué candidatos al puesto de astronauta pueden contratar para el programa. Solo tendrían que rechazar a aquellos que, según el modelo anterior, tuviesen una probabilidad inferior a la que considerasen adecuada como punto de corte.

Ahora bien, una vez admitidos, falta decidir qué rol desempeñarán durante el vuelo: comandante, especialista de misión o piloto. Para ello cuentan con otro conjunto de 15 astronautas con los resultados de otra prueba de evaluación, que podéis ver en la siguiente figura.

A los ingenieros, contentos con el buen resultado que les dio el modelo de regresión logística binaria, lo primero que se les ocurre es hacer algo parecido, pero, como hay tres categorías en la variable que se quiere predecir (ya no es binaria), optan por la llamada estrategia de todos contra uno.

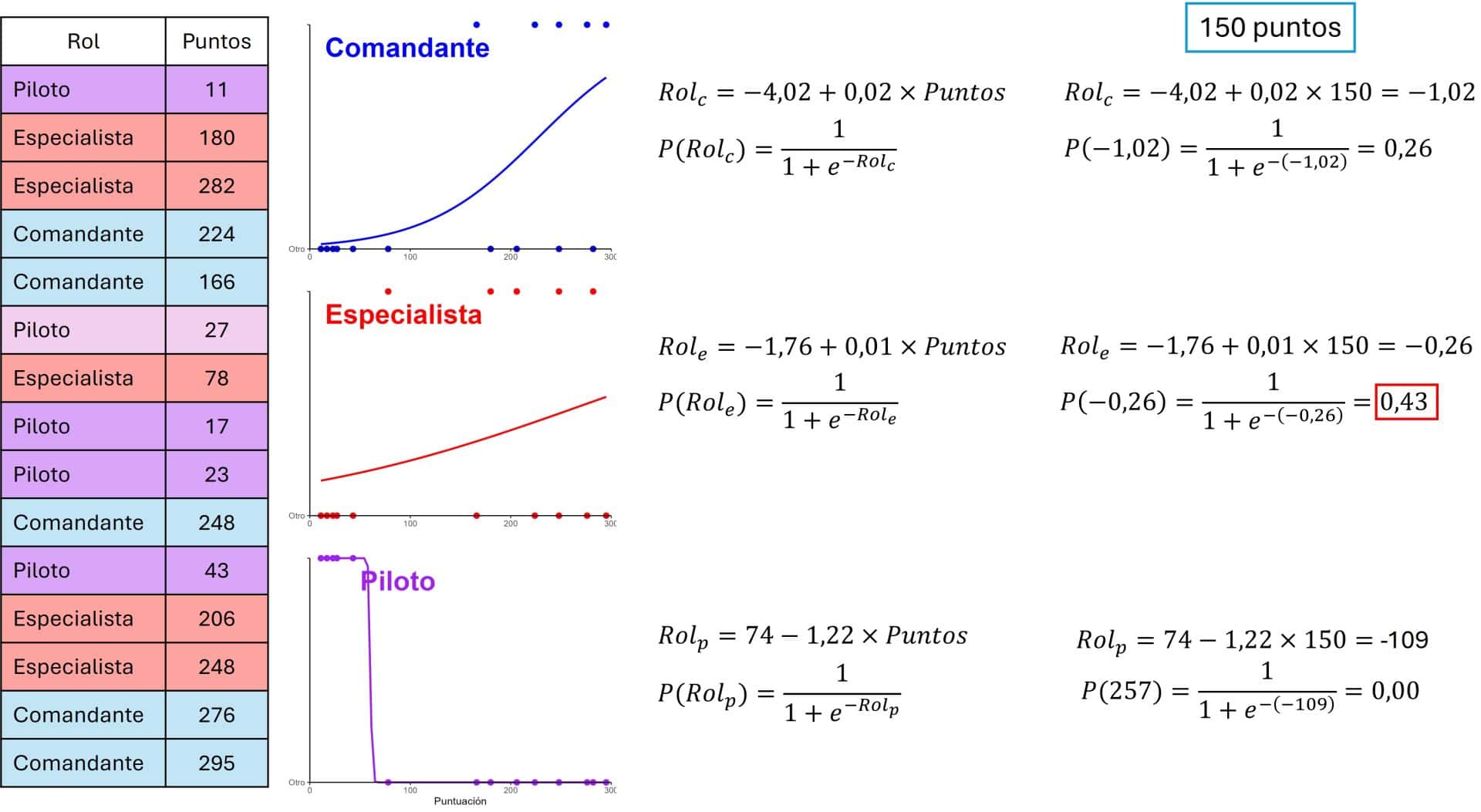
Esta consiste en construir tres modelos de regresión binaria, agrupando dos categorías como una sola en cada uno de los modelos. En el primero, el objetivo se codifica como comandante (1) u otro (0). En el segundo se marca el 1 como especialista y el 0 como la combinación de los otros dos y, en el tercero, el 1 como piloto y el 0 los otros dos. Podéis ver todo el proceso en la figura anterior.

Lo primero que hacen es calcular los tres modelos. Una vez hecho esto, se plantean qué rol sería el más adecuado para un astronauta que obtiene 150 puntos en la prueba. Sustituyen el valor de la puntuación por 150 y calculan el resultado para cada caso.

Por ejemplo, en el caso del primer modelo, el de comandante, obtenemos un valor de -1,02. Para calcular la probabilidad de que el rol de comandante sea el ideal, introducimos este valor en la ecuación de la transformación logística que hicimos para construir el modelo de regresión logística, como ya explicamos más arriba.

La función sigmoide nos arroja un valor de probabilidad de 0,26. Una vez hecho este cálculo con los tres modelos, nos quedaríamos con el que dé el valor máximo que, en este caso, es el de especialista, que nos da un valor de 0,43.

En conclusión, si un candidato obtiene esta puntuación en la prueba, el puesto para el que es más probable que desempeñe una buena función será el de especialista de misión. Puede que incluso fuese un aceptable comandante, pero, desde luego, parecería poco apto para ser el piloto de la misión.

Llegados a este punto, pensaréis que los ingenieros han solucionado con elegancia el problema, pero la verdad es que las cosas pueden hacerse mejor. El problema es que han calculado el puesto que quizás sea el mejor para el candidato, pero no pueden estimar con qué probabilidad.

Si os fijáis, las valores que nos dan los tres modelos no suman 1, lo que significa que no representan probabilidades directas de pertenecer a cada categoría de la variable que se quiere predecir. Para conseguir este objetivo, cuando la variable tiene más de dos categorías, no podemos utilizar la función logística o sigmoide, como hacíamos con las variables binarias. En estos casos hay que recurrir a otra función un poco más compleja, la función softmax.

La extensión más allá de lo binario

La función softmax es una generalización de la sigmoide que nos sirve para la clasificación multiclase, ya que su objetivo es convertir el conjunto de valores de probabilidad para que sumen 1. Esto facilita la interpretación de los resultados en términos de categorías.

En la siguiente figura podéis ver su expresión. A diferencia de la función sigmoide, la softmax divide por la suma de los resultados de los tres modelos (calculados con sus log-odds).

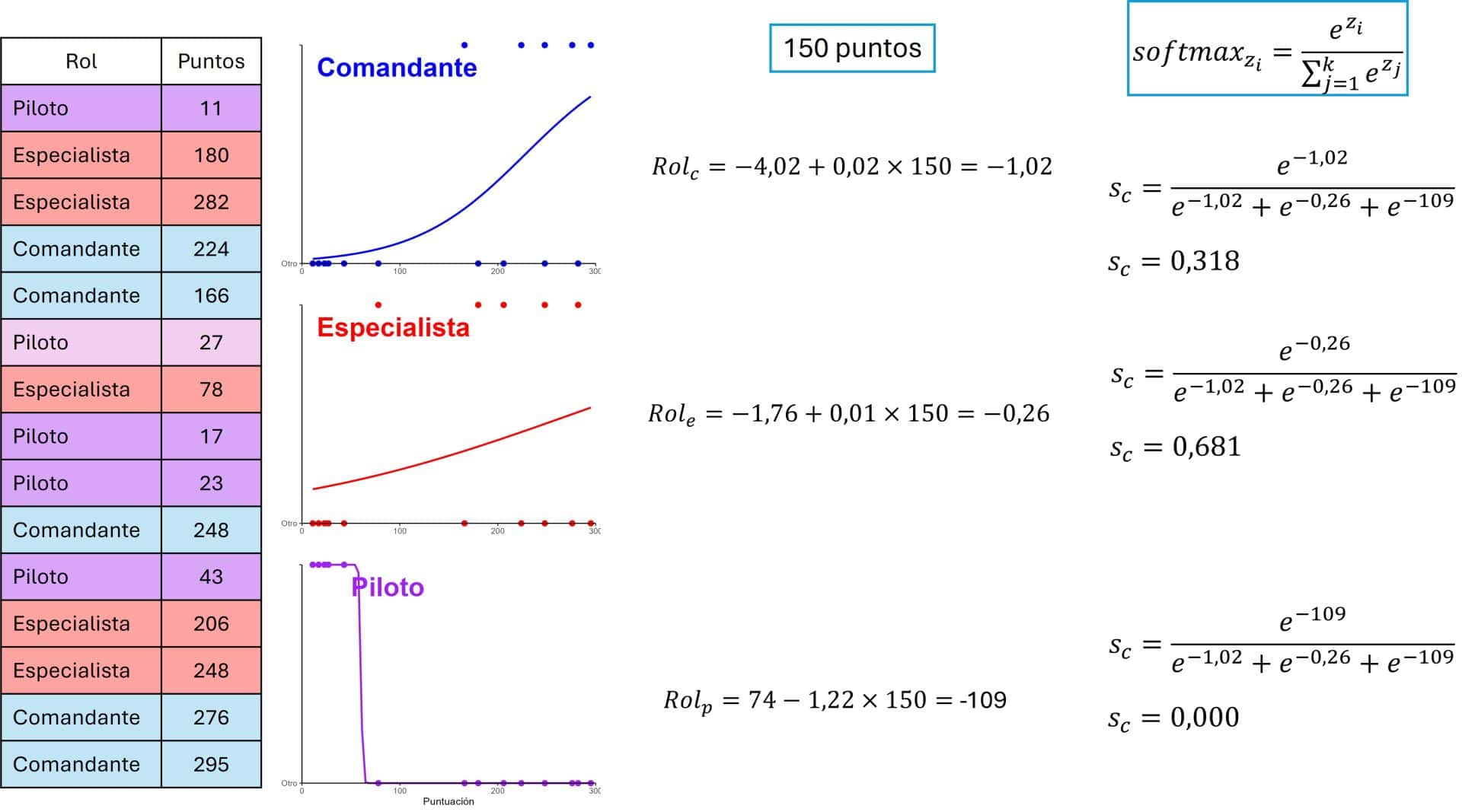
Fijaos que, ahora, los resultados de las tres categorías suman 1 (en realidad suman 0,99 pero ya sabéis, los problemas del redondeo). Ahora ya sabemos que la probabilidad de que un candidato con 150 puntos desempeñe un buen papel como especialista es del 68%, algo más del doble que la de ser un buen comandante. Y, desde luego, no lo pongáis a pilotar.

Regresión logística multinomial

Todo lo que hemos visto hasta ahora sirve para ver cómo podemos calcular las probabilidades de pertenecer a una determinada categoría de una variable nominal cuando tratamos con variables de más de dos categorías.

De todo lo que hemos hablado surge la técnica que habitualmente se utiliza cuando necesitamos hacer clasificación multiclase, que no es otra que la regresión logística multinomial.

La regresión logística multinomial calcula k-1 modelos diferentes (siendo k el número de categorías de la variable a predecir) con lo que, en nuestro ejemplo, solo tenemos que ajustar dos modelos, ya que uno de ellos se tomará como modelo de referencia (en seguida veremos porqué solo dos y no tres).

Para hacerlo, a cada modelo le restamos los parámetros del modelo que tomemos como referencia que, en nuestro caso, será el de comandante. Podéis ver los cálculos en la figura siguiente.

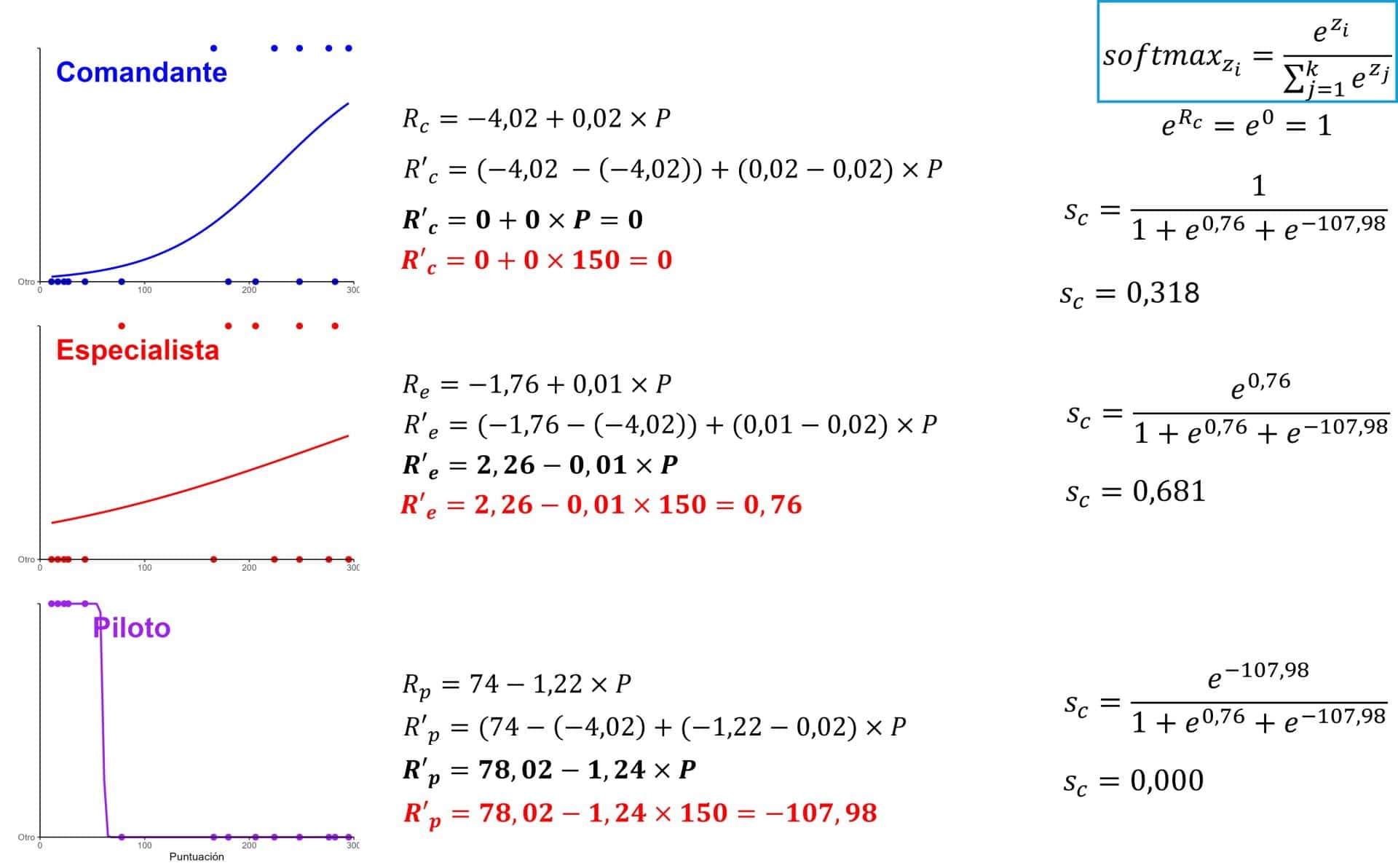
Ahora, con los nuevos modelos podemos aplicar la función softmax para calcular las probabilidades de cada categoría para una puntuación de 150. Como no podía ser de otra forma, llegamos a los mismos valores de probabilidad, pero fijaos en una cosa interesante.

Como la log-odds del modelo de referencia es 0, su contribución en la función softmax es e⁰ = 1. Por lo tanto, las probabilidades solo dependen de las log-odds de los otros dos modelos. Esto es lo que permite a la regresión logística multinomial tomar una categoría como referencia y ajustar k-1 modelos para estimar las k probabilidades.

El camino más rápido

Sobra decir que todos estos cálculos los hemos hecho para divertirnos un poco, porque cuando tengamos que resolver un problema similar recurriremos a un programa estadístico que lo hará en un abrir y cerrar de ojos.

Yo lo he hecho con R. Podéis verlo en el script que os comenté al principio de esta entrada.

Para interpretar los resultados del programa, habrá que tener en cuenta que nos dará los resultados del especialista respecto al comandante y del piloto respecto al comandante, por separado (comandante se usa como referencia para los dos).

Por ejemplo, para el especialista nos dice que el intercepto es 2,83 y el coeficiente para la puntuación es -0,01. Este coeficiente nos indica que el aumento de una unidad de la puntuación disminuye la probabilidad de que sea especialista frente a que sea comandante.

Además, podemos calcular la odds ratio haciendo el antilogaritmo del coeficiente. Así e^-0,01 = 0,99. Una odds ratio menor que 1 nos indica que a mayor puntuación será menos probable que sea especialista y más probable que sea comandante.

En resumen, los valores más altos de puntuación se asocian con una mayor probabilidad de que estemos ante un futuro comandante que ante un futuro especialista de misión.

Claro que todo esto solo podemos concluirlo validando el modelo de regresión, comprobando que sea significativo y esos detalles a los que no hemos prestado atención porque no son el tema de hoy, pero que son muy importantes.

Nos vamos…

Y aquí dejamos esta larga carrera espacial por el día de hoy.

Hemos visto cómo la función sigmoide, muy útil para estimar probabilidades en la clasificación binaria, no permite el cálculo de probabilidades directas en la clasificación multiclase, algo de lo que sí es capaz su versión extendida, la función softmax.

Y esto no se aplica solo a la regresión logística, binaria o multinomial, sino que tiene también su paralelismo en las redes neuronales artificiales que realizan clasificación. En efecto, la última capa de la red elegirá como función de activación la sigmoide o la softmax, dependiendo de que se realice clasificación binaria o multiclase. Pero esa es otra historia…