Probabilidad binomial.

La probabilidad binomial mide el número de éxitos de una serie de sucesos de con una determinada probabilidad de éxito de cada suceso.
Saber cocinar es una ventaja. ¡Qué bien queda uno cuando tiene invitados y sabe cocinar como es debido!. Te pasas dos o tres horas comprando los ingredientes, te dejas un dineral y te tiras otras dos o tres horas en la cocina… y, al final, resulta que el plato estupendo que estabas preparando te queda hecho una ruina.
Y esto le pasa hasta a los mejores cocineros. Nunca podemos estar seguros de que el plato nos vaya a quedar bien, aunque lo hayamos preparado antes muchas veces. Así que entenderéis el problema que tiene mi primo.
El problema del cocinero
Resulta que va a dar una fiesta y a él le ha tocado hacer el postre. Sabe hacer un pastel bastante rico, pero solo le sale realmente bueno la mitad de las veces que lo intenta. Así que está muy preocupado por hacer el ridículo en la fiesta, como es bien comprensible. Claro que mi primo es muy listo y ha pensado que si hace más de un pastel, alguno le tiene que quedar bueno. Pero, ¿cuántos tiene que hacer para tener, por lo menos, uno bueno?.
El problema de esta pregunta es que no tiene una respuesta exacta. Cuantos más pasteles haga, más probable que alguno salga bueno. Pero claro, puede hacer doscientos y tener la mala suerte de que todos sean malos. Pero no desesperéis: aunque no podemos dar una cifra con seguridad absoluta, si podemos medir la probabilidad de quedar bien con un número determinado de pasteles. Veámoslo.
Distribución de probabilidad binomial
Vamos a imaginar la distribución de probabilidad, que no es más que el conjunto de situaciones que incluyen todas las situaciones que pueden ocurrir. Por ejemplo, si mi primo hace un pastel, éste puede salir bueno (B) o malo (M), ambos con una probabilidad de 0,5. Podéis verlo representado en el gráfico A. Tendrá un 50% de probabilidades de éxito.
Si hace dos pasteles puede ocurrir que le salgan bien uno, dos o ninguno. Las combinaciones posibles serán: BB, BM, MB, MM. La probabilidad de tener uno bueno es de 0,5 y la de tener dos 0,25, con lo que la probabilidad de tener al menos uno bueno es de 0,75 o 75% (3/4). Lo representamos en el gráfico B Vemos que las opciones mejoran, pero todavía queda mucho margen para el fracaso.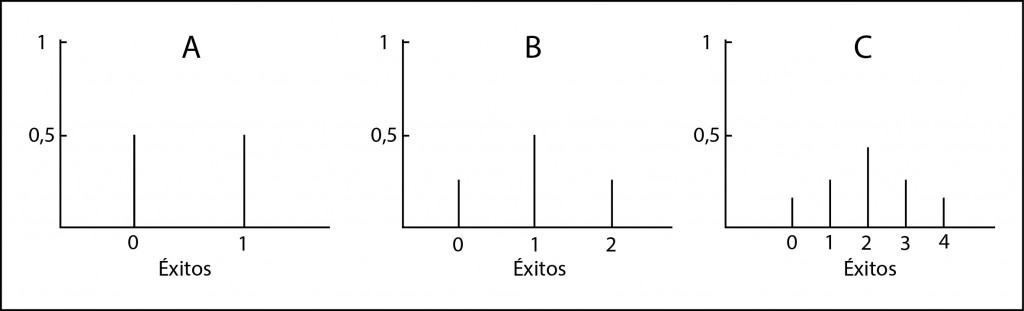
Si hace tres pasteles las opciones son las siguientes: BBB, BBM, BMB, BMM, MBB, MBM, MMB y MMM. Esto mejora, ya tenemos un 87,5% (1/8) de que al menos un pastel salga bien. Lo representamos en el gráfico C.
¿Y si hace cuatro, o cinco, o…?. El asunto se convierte en un auténtico coñazo. Cada vez es más difícil imaginar las combinaciones posibles. ¿Y qué hacemos?. Pues pensar un poco.
Si nos fijamos en los gráficos, las barras representan los elementos discretos de probabilidad de cada uno de los eventos posibles. Según aumenta el número de posibilidades y aumenta el número de barras verticales, la distribución de las barras comienza a adoptar una forma acampanada, ajustándose a una distribución de probabilidad conocida, la distribución binomial.
Sucesos de Bernouilli
Las personas que entienden de estas cosas, llaman experimentos de Bernouilli a aquellos que tienen solo dos soluciones posibles (son dicotómicos), como tirar una moneda (cara o cruz) o nuestro pastel (bueno o malo). Pues bien, la distribución binomial mide el número de éxitos (k) de una serie de experimentos de Bernouilli (n) con una determinada probabilidad de ocurrencia de éxito de cada suceso (p).
En nuestro caso la probabilidad es p=0,5 y podemos calcular la probabilidad de tener éxito repitiendo el experimento (cocinando pasteles) según la siguiente fórmula:
Si sustituimos p por 0,5 (la probabilidad de que el pastel salga bueno), podemos ir jugando con los valores de n para obtener, al menos, un pastel bueno (k≥1).
Si hacemos cuatro pasteles, la probabilidad de tener al menos uno bueno es de 93,75% y si hacemos cinco esta probabilidad sube a 96,87%, un valor de probabilidad razonable para lo que estamos buscando. Yo creo que haciendo cinco pasteles es muy difícil que a mi primo se le arruine su fiesta.
También podríamos despejar el valor de la probabilidad y calcularlo al revés: dado un valor de P(k de n) obtener el número de intentos necesarios. Otra cosa que se puede hacer es calcular todas estas cosas sin utilizar la fórmula, sino usar cualquiera de las calculadoras de probabilidad disponibles en Internet.
Nos vamos…
Y aquí se acaba esta entrada tan golosa. Existen, como podéis imaginar, más tipos de distribuciones de probabilidad, tanto discretas como esta distribución binomial como continúas como la distribución normal, la más famosa de todas. Pero esa es otra historia…
