Binomial probability.

Binomial probability measures the number of successes of a series of events with a given probability of success for each event.
Knowing how to cook is a plus. What in good terms you stay when you have guests and you know how to cook properly!. It takes you two or three hours to buy the ingredients, you spend a fortune in it, and it takes another two or three hours working in the kitchen… and, in the end, it turns out that your great dish you were preparing ends up as a wreck.
And this may happen even to best cookers. We can never be sure that our dish will turn out good, although we have prepared it many times before. So you will understand the problem with my cousin.
The cooker’s dilemma
As it happens, he’s going to give a party and the dessert has been his lot. He knows how to do a pretty and tasty cake, but it only turns out really good half of the times he tries. So he’s very concerned about making fool of himself at the party, as it’s easy to understand. Of course, my cousin is very clever and has thought that, if he makes more than one cake, at least one of them will turn out good. But how many cakes does he have to do to get at least one good?.
The problem with this question is that it doesn’t have an exact answer. The more cakes we make, the more likely one of them turns out good. But, of course, you can make two hundreds cakes and have the bad luck that all of them turn out bad. But do not despair: although we cannot give a number with absolute certainty, we can measure the probability of getting along with a certain number of cakes. Let’s see it.
Binomial probability distribution
We are going to imagine the probability distribution, which is just the set of situations that include all the possible situations that may occur. For example, if my cousin makes one cake, it can turns out good (G) or bad (B), both of them with a probability of 0.5. You can see it represented in Figure A. He’ll have a 50% chance of success.
If he makes two cakes it may be that he gets one cake good, two or none. The possible combinations are: GG, GB, BG, and BB. The chance of coming up with a good one is 0.5, and 0.25 the chance of getting two good ones, so the probability of getting at least one cake good is 0.75 or 75% (3/4). It’s represented in Figure B. We see that options have improved, but it’s still much room for failure.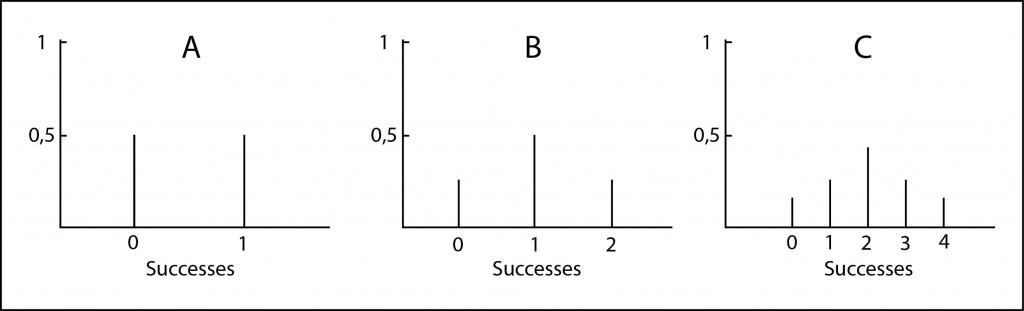
If he makes three cakes, the options will be: GGG, GGB, GBG, GBB, BGB, BGG, BBG, and BBB. The situation is improving, we have an 87.5% (1/8) of probabilities to get at least one cake. We represent it in Figure C.
And what if he makes four cakes, or five, or…?. The issue becomes a pain in the ass. It’s increasingly difficult to imagine all the possible combinations. What can we do?. Well, we can think a little.
If we look at the graphs, the bars represent the discrete elements of the probability of each of the possible events. As the number of possibilities and the number of vertical bars increase, the bars distribution begins to take a bell shape, conforming to a known probability distribution, the binomial distribution.
Bernouilli’s events
People who know about this stuff called Bernouilli experiments to those who have only two possible solutions (are dichotomous), like flipping a coin (heads or tails) or making our cakes (good or bad). However, the binomial distribution measures the number of successes (k) of a series of Bernouilli experiments (n) with a certain probability of success of each event (p).
In our case the probability is p = 0.5 and we can calculate the probability of success by repeating the experiment (cooking cakes) using the following formula:
If we replace p by 0.5 (the probability of the cake comes out good), we can play with different values of n to obtain the probability of getting at least one good cake (k ≥ 1).
If we make four cakes, the probability of having at least one good is of 93.75% and if we make five the probability increases to 96.87%, a reasonable probability for what we are dealing with. I believe that if my cousin makes fives cakes it will be very difficult for him to ruin his party.
We could also clear up the value of the probability and calculate the reverse: given a value of P(k,n), get the number of attempts needed. Another thing you can also do is to calculate all these things without using the formula, but using any probability calculator available online.
We’re leaving…
And this is the end of this tasty post. There are, as you can imagine, more types of probability distributions, both discrete as the binomial and continuous as the normal distribution, the most famous of all of them. But that’s another story…
