Análisis de componentes principales.

Si habéis visto Interstellar, la película de Christopher Nolan, seguramente recordaréis ese momento cumbre en el que Cooper se mete en un agujero negro y acaba flotando en un teseracto detrás de la estantería de su hija. Allí está él, intentando comunicar datos cuánticos complejos sobre la gravedad a través de un reloj de pulsera, usando algo tan rudimentario como el código morse. Es la definición perfecta de la frustración: tienes una realidad inmensa, compleja y llena de dimensiones extrañas, pero solo tienes un canal limitado para explicarla sin que a la pobre Murph le estalle la cabeza. ¿Cómo comprimes la complejidad del universo en el tictac de un segundero?

Ese drama de ciencia ficción es, irónicamente, el pan de cada día en el análisis de datos. Vivimos bombardeados por variables: edad, peso, altura, nivel de colesterol, likes en Instagram, horas de sueño… Si intentamos analizarlo todo a la vez, acabamos como Cooper: gritando en el vacío mientras el resto del mundo nos mira raro. A veces, tantas variables no hacen más que meter ruido, repitiendo lo mismo con distintas palabras. Necesitamos una forma de simplificar, de encontrar la fuerza gravitatoria que une esos datos dispersos y proyectarlos en una realidad que podamos pintar en un folio (o en una estantería, para el caso).

Aquí es donde los estadísticos, que son los verdaderos viajeros del espacio-tiempo, aunque con menos presupuesto para efectos especiales, sacan su herramienta para la ocasión: el análisis de componentes principales (ACP). Al igual que el teseracto simplificaba las dimensiones para que Cooper pudiera volver del agujero negro, el ACP toma el caos de datos multidimensionales y lo aplana, quedándose solo con lo que más le importa: la varianza.

Preparaos, porque en esta entrada vamos a reducir dimensiones sin necesidad de acercarnos a una singularidad gravitatoria como Gargantúa.

Análisis de componentes principales: la obsesión por la sombra perfecta

Para entender cómo funciona el ACP, tenéis que soltar la calculadora y activar la imaginación. Visualizad un patito de goma gigante. Sí, uno de esos amarillos chillones que usaría Godzilla si decidiera darse un baño de espuma. Imaginad que tenéis este majestuoso objeto tridimensional flotando en el aire y vuestra misión es explicarle a Plani, un ser bidimensional ficticio (vamos, un folio con patas), que jamás ha visto el volumen, qué es un pato de goma. Vuestra única herramienta es un foco de luz para proyectar la sombra del pato en la pared.

Si sois unos fotógrafos nefastos y ponéis el foco apuntando hacia la cabeza del pato, la sombra que proyectaréis será… un óvalo amorfo. Habréis reducido las dimensiones (de 3D a 2D), sí, pero os habréis cargado la información vital: Plani pensará que un pato es una mancha de mostaza o una patata pocha. Habéis elegido una proyección con muy poca información y nula distinción.

Sin embargo, si os esforzáis un poco y rotáis el pato hasta iluminarlo perfectamente de perfil, la sombra revelará esa silueta inconfundible con su pico, su cola respingona y esa sonrisilla de suficiencia que tienen los patos de goma. Esa es la «mejor sombra», la que conserva la esencia y la dignidad del pato original, al mismo tiempo que reduce su dimensión desde nuestro mundo tridimensional al mundo bidimensional de Plani.

Pues bien, el ACP no es más que un fotógrafo matemático obsesivo que se dedica a girar los datos hasta encontrar el ángulo exacto donde la sombra proyectada sea lo más grande, nítida y detallada posible, evitando que el pato parezca una patata.

Navegando por intuición

Una vez entendido que buscamos la mejor sombra posible para no hacer el ridículo, bajemos de la abstracción de los juguetes de baño a la realidad de los datos para intentar ver, de forma gráfica, cómo funciona el ACP.

Imaginad que tenemos datos sobre la salud de mil astronautas, entre otros, su presión sistólica y su presión diastólica. Si representamos estos datos en una gráfica, veremos que los puntos no están dispersos al azar, sino que forman una especie de nube alargada. Esto ocurre porque ambas variables están correlacionadas: si te sube la tensión alta, suele subirte la baja.

Podéis verlo en la figura adjunta. Los valores de presión diastólica en función de la sistólica varían en dos direcciones. La más importante es la dirección ascendente que sigue la nube de puntos, hacia arriba y hacia la derecha. Cuanto mayor es la presión sistólica, mayor es la diastólica.

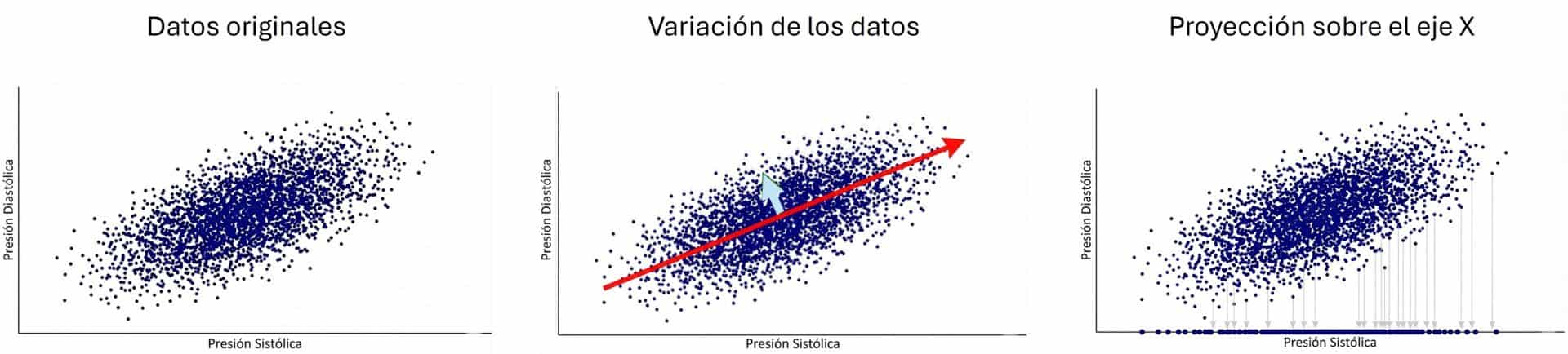
Pero, si os fijáis bien, también varían en una segunda dirección, perpendicular a la anterior (ortogonal, para ponernos finos), que es la que da “grosor” a esa especie de balón de rugby alargado que forma la nube de puntos. Os lo muestro en el gráfico con los dos vectores que he dibujado. El vector rojo (el largo) representa la tendencia general: la relación fuerte entre ambas presiones. El vector azul (el corto) representa la variabilidad restante, las pequeñas desviaciones individuales de esa norma general.

Ahora, pensemos cómo podríamos simplificar estos datos, cómo encontrar la sombra más informativa. Supongamos que queremos reducirlos a una sola dimensión, en lugar de las dos que tienen en la actualidad (sobra decir que, en la realidad, no haríamos tal cosa con unos datos tan simples, pero es para poder representarlo y entenderlo mejor).

Si intentamos simplificar proyectando todos los puntos al eje horizontal original (eje X, presión sistólica) o al vertical (eje Y, presión diastólica), perderemos información valiosa. ¿Por qué? Imaginad que aplastáis ese balón de rugby contra la pared del eje X. Al hacerlo, ignoráis la contribución de la otra variable. Peor aún, si hubiera grupos distintos de astronautas (digamos, tres clústeres clínicos diferentes), al proyectarlos tontamente sobre un eje original, estos grupos podrían solaparse y mezclarse, haciendo imposible distinguirlos. Estaríamos combinando poblaciones diferentes y perdiendo la estructura real de los datos, como ocurría al iluminar el patito de goma desde arriba.

Siempre que simplifiquemos perderemos algo de información, pero debemos esforzarnos para no perder la estructura real, que es la que tratamos de determinar con más facilidad con la reducción de las dimensiones iniciales.

Aquí es donde el ACP propone algo más inteligente. En lugar de resignarnos a usar los ejes que nos vienen con los datos originales (sistólica y diastólica), vamos a rotar el sistema de coordenadas para ver qué conseguimos.

Primero, centramos los datos restando la media a cada uno, moviendo la nube para que su centro esté en el origen (0,0). Una vez centrados, buscamos una nueva dirección (la flecha roja en el gráfico) que atraviese la nube de puntos exactamente por su parte más larga. Matemáticamente, buscamos la línea donde, si proyectamos los puntos, estos queden lo más separados posible entre sí. Esa dirección es la que recoge una cantidad mayor de la varianza de los datos (donde los datos están más esparcidos).

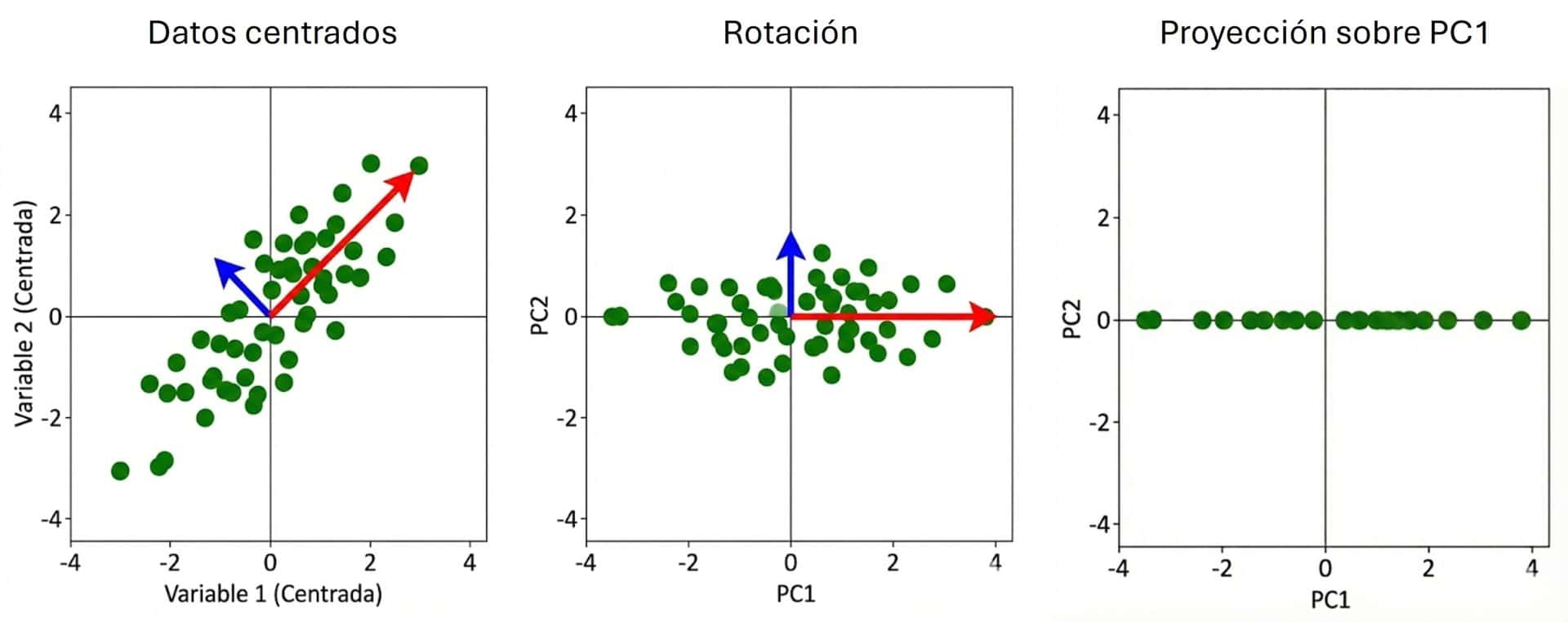
Finalmente, rotamos todo para que esa flecha roja se convierta en nuestro nuevo eje X, que bautizaremos pomposamente como primera componente principal (PC1). Fijaos en la magia: esta PC1 no es ni la presión alta ni la baja, sino una combinación lineal de ambas (un poco de sistólica más un poco de diastólica) que captura la «esencia» de la presión arterial general. De hecho, en ejemplos como este, la PC1 suele capturar la inmensa mayoría de la información (a veces más del 97% de la varianza total).

Luego, buscamos una segunda dirección que debe cumplir una regla de oro: tiene que ser perpendicular a la primera. Esa es la flecha azul de nuestro segundo gráfico (en el que he disminuido el número de puntos para que se visualice mejor). Esta dirección explicará «lo que queda», esa varianza residual que da el ancho al balón de rugby. Esa será nuestra segunda componente principal, PC2.

Al final, lo que hacemos es rotar la «cámara» con la que miramos los datos. Pasamos de verlos desde el ángulo de «sistólica vs. diastólica» a verlos desde el ángulo de «presión arterial general (PC1) vs. desviación específica (PC2)». Y como la PC1 es tan buena resumiendo la película, a menudo podemos permitirnos el lujo de borrar la PC2 y quedarnos con una sola dimensión, habiendo perdido poquísima información en el proceso.

Cooper se pone a hacer números

Ahora vamos a traducir a números lo que hemos entendido de forma gráfica. A fin de cuentas, Cooper no se metió en un agujero negro para que nosotros nos asustemos ahora por un par de sumas y restas.

Vamos a analizar un ejemplo totalmente ficticio, pero que podría ser muy importante para la supervivencia de la misión Endurance: la idoneidad de los planetas candidatos.

Nos vamos a permitir una licencia poética y vamos a imaginar que TARS (ese robot tan listo) ha escaneado 15 planetas potenciales y nos da dos datos clave para saber si la humanidad puede vivir allí o si moriremos aplastados en cinco minutos. Podéis ver los datos en la tabla adjunta, que muestra la gravedad (G), en m/seg², y la dilatación temporal (DT), cuántos años pasan en la Tierra por cada hora que pasa en el planeta (sí, el famoso «una hora aquí son siete años allí»).

Si miráis la tabla de abajo, veréis una tendencia clara, a la par que aterradora: los planetas con mayor gravedad suelen estar más cerca de Gargantúa, por lo que tienen una dilatación temporal más bestia. Existe una correlación positiva… y peligrosa para Cooper y sus compañeros.

Por ejemplo, el planeta Miller (M) tiene una gravedad aplastante de 22 (recordad que la de la Tierra es de 9,8) y una dilatación de 7 años por hora. Un infierno. En el otro extremo, el planeta Edmunds (N) es mucho más amable. A Cooper le interesa calcular algún parámetro que le ayude a valorar los dos datos que tiene de cada planeta, para así elegir con más facilidad cuál puede ser el más compatible con el éxito de la misión.

Así que decide recurrir al ACP, que le va a ayudar a resumir estas dos columnas en un solo número que, en un alarde de creatividad, bautiza como índice de hostilidad (IH).

Lo primero que hace es coger toda la nube de datos planetarios y moverla para que el centro esté en el origen de coordenadas, como vimos más arriba con los gráficos. Calcula la media de G (15,67) y la media de DT (6,26) y se la resta a cada planeta. Podéis ver todo el proceso del cálculo numérico en las tablas.

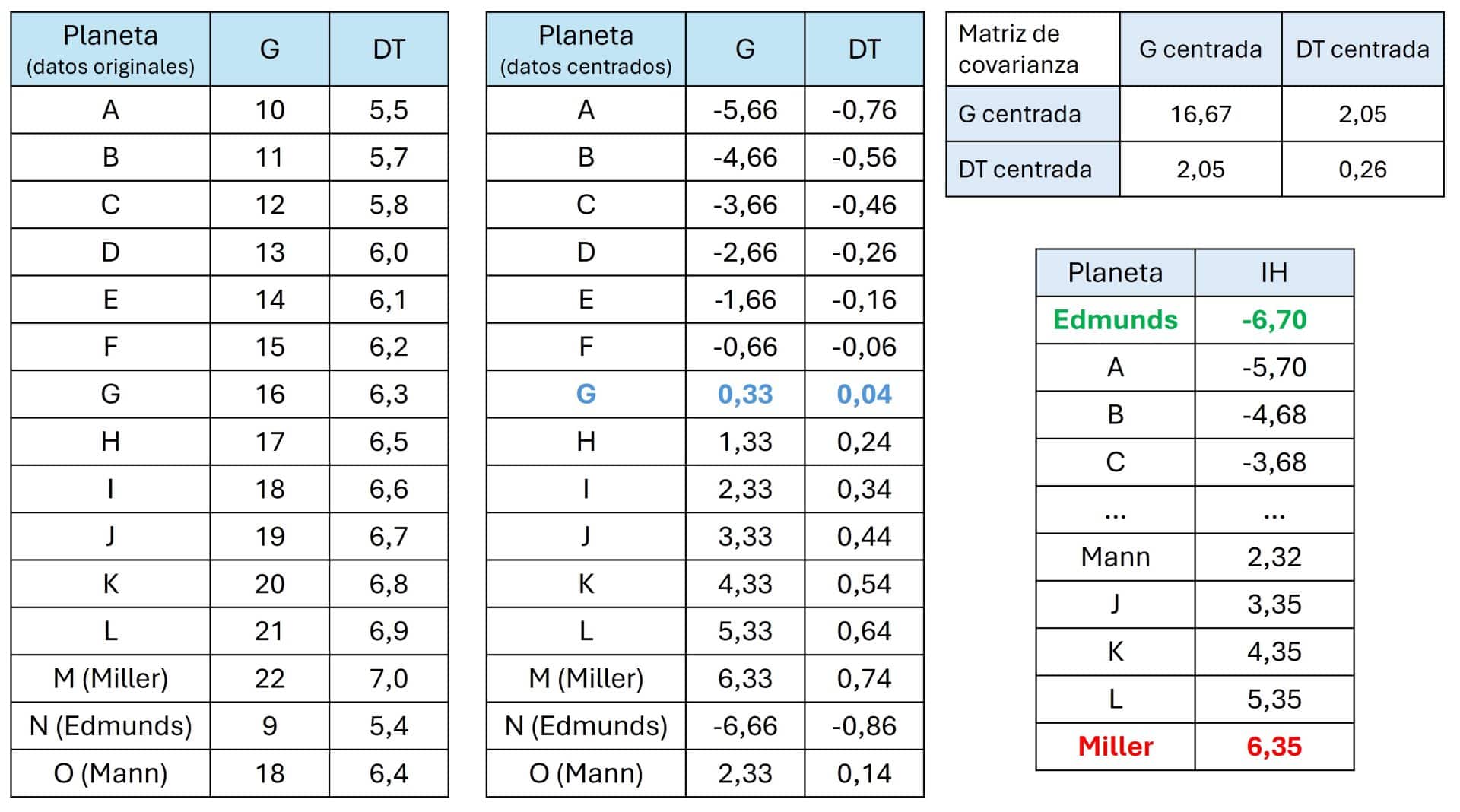
Ahora, los valores negativos significan planetas «más seguros que la media» y los positivos son «trampas mortales». El planeta G es el término medio, ni fu ni fa. Si tiene aire respirable puede ser ideal, siempre que no huela a calcetín sudado.

El segundo paso es el cálculo de la matriz de covarianzas, nuestro tejido espacio-temporal. Básicamente, es una tabla que TARS le escupe para decirle cómo se relacionan las variables. En la diagonal principal vemos las varianzas, que nos dicen que la gravedad (16,67) varía mucho más en nuestros datos que la dilatación temporal (0,26). El resto de los números son las covarianzas entre las dos variables. Al ser positiva (2,05), confirma que, a más gravedad, más tiempo perderá Murph esperando a que vuelva su padre.

A partir de este momento es cuando Cooper empieza a sudar un poco: en su manual de instrucciones dice que tiene que calcular los eigenvalores y los eigenvectores.

Para que no os explote la cabeza con el álgebra, recordad las flechas de los primeros gráficos que os mostré más arriba.

Pues bien, los eigenvectores son, literalmente, las direcciones en la que apuntan (la flecha roja cruzando la nube a lo largo y la flecha azul a lo ancho). Por otro lado, los eigenvalores son, simplemente, los números que nos dicen la «fuerza» o longitud de esas flechas, es decir, cuánta información capturan. La flecha roja (PC1) tiene un eigenvalor grande (porque explica casi toda la varianza de los datos), mientras que la flecha azul (PC2) tiene uno ridículo, porque apenas cubre distancia ni aporta nada nuevo.

El ordenador de la nave hace los cálculos y obtiene que la PC1 tiene un eigenvalor de 16,92 (enorme) y un eigenvector cuyas coordenadas son (0,99, 0,12). Esta componente apunta casi todo en la dirección de la gravedad, pero también arrastra consigo la dilatación. Si vemos la PC2, su eigenvalor es 0,004 (puro polvo estelar insignificante) y su eigenvector apunta hacia (0,12, -0,99).

¿Cómo interpretamos esto? Imaginad que toda la información que tenemos sobre los planetas es un pastel. El tamaño total de ese pastel (varianza total) es la suma de todos los eigenvalores (16,92 + 0,004). Si queremos saber cuánto pastel se come nuestra primera componente principal, solo tenemos que dividir su parte entre el total:

Varianza explicada por PC1 = 16.92 / (16.92 + 0.004) = 0.9997

Un resultado sorprendente. Dicho en porcentaje, el 99,97% de la información sobre la hostilidad del planeta está capturada en la primera componente. La segunda componente es solo un 0,03% de ruido, totalmente irrelevante para decidir dónde aterrizar.

Bien, a Cooper ya solo le queda tomar una decisión: ¿en qué planeta aterriza? Pero antes, TARS tiene que convertir esos pares de datos (G y DT) en una sola nota final. ¿Cómo lo hace?

Aquí volvemos a presenciar la magia del ACP. No es que proyecte los puntos con un cañón láser sobre la nueva dirección de la componente; lo que hace es crear un nuevo modelo matemático, muy parecido a una ecuación de regresión. El ACP construye una fórmula para calcular nuestro índice de hostilidad (PC1) mezclando las dos variables originales según la importancia que les dio sus eigenvectores, que se convierten en los parámetros del modelo.

Así, multiplicamos la gravedad (centrada) por 0,99, multiplicamos la dilatación temporal (centrada) por 0,12, sumamos ambos resultados y… ¡voilá! tenemos el IH.

Por ejemplo, miremos el terrorífico planeta Miller: tenía una gravedad centrada de 6,33 y una dilatación temporal centrada de 0,74. Si aplicamos la fórmula anterior, su IH = 6,35.

Al aplicar esta fórmula a todos los planetas, hemos simplificado el universo. En la última tabla podéis ver el ranking definitivo de hostilidad(la puntuación son los valores de la PC1) calculado por TARS.

¿Qué hemos conseguido? En lugar de mirar dos variables y discutir sobre si es peor la gravedad o perderse la infancia de tus hijos, ahora tenemos un único número calculado matemáticamente, la PC1, que resume la «dureza del planeta». El planeta Miller tiene un 6,35 (puro peligro). El planeta Edmunds tiene un -6,70 (el nuevo hogar).

Eso es lo que hace el ACP: comprimir la complejidad del universo en algo que quepa en un mensaje de código morse a través de un reloj. Murph estaría orgullosa.

SVD: el agujero de gusano matemático

El ejemplo que hemos visto hasta ahora es ridículamente simple, pero si queremos representarlo gráficamente y hacer los números a mano, ha de ser así por fuerza. Sin embargo, en la realidad los conjuntos de datos son mucho más grandes y tienen un número de variables mucho mayor. Aquí es donde brilla el ACP, resumiendo la varianza (o una gran parte de ella) generada por decenas o cientos de variables en dos o tres componentes principales.

No hace falta decir que todo esto se hace utilizando un ordenador y un programa informático, como puede ser el programa R, que puede realizar todos estos pasos si se opta por el camino largo de la matriz de covarianza, los eigenvectores y eigenvalores, etc. Sin embargo, existe también un atajo más elegante y menos costoso desde el punto de vista computacional, que es el método de la descomposición en valores singulares (SVD, por sus siglas en inglés).

El método SVD es numéricamente más estable y evita errores de redondeo porque trabaja directamente con la matriz de datos, sin tener que calcular primero la covarianza. La idea es que la matriz de datos centrados (X) se puede descomponer en tres matrices mágicas:

X = U · D · V^T

No os dejéis impresionar por el álgebra lineal. Vamos a traducir esto a un idioma más sencillo.

V^T es la matriz transpuesta de los eigenvectores, así que contiene los vectores que indican hacia dónde rotar el mapa para alinear nuestros ejes con la máxima información. Básicamente, les dice a los datos: giraos 30 grados a la derecha (por ejemplo), que ahí es donde está la máxima varianza.

D es un elemento nuevo hasta ahora, una matriz diagonal que contiene los famosos valores singulares, que forman una especie de factor de escala que determina cuánto se estiran o comprimen los datos en esas nuevas direcciones. Si el valor es grande, esa dirección es una autopista de información importante; si es pequeño, es un sendero de cabras (ruido) que podemos ignorar.

Por último, la matriz U es el mapa de proyección de los datos. Una vez que hemos girado y estirado los datos, esta matriz nos dice exactamente dónde cae cada punto en este nuevo sistema. Son las coordenadas finales normalizadas.

Ya podemos entender la fórmula de antes. Simplemente nos dice que los datos originales (X) son el resultado de tomar una posición en el mapa (U), estirarla según su importancia (D) y rotarla para que encaje en la realidad (V^T)de la nueva componente principal.

Nos vamos…

Y con esto vamos a montarnos en el teseracto para salir de la brana y aprovechar la cuarta dimensión para volver desde Gargantúa hasta casa antes de que se nos haga de noche. O sea, que vamos a ir terminando.

Hemos visto que, ya sea evitando patos amorfos o eligiendo un planeta que no nos mate en cinco minutos, el secreto no siempre está en acumular montañas de datos, sino en saber encontrar el ángulo perfecto, esa sombra nítida que nos cuente la historia real ignorando el ruido de fondo. Al final, el ACP no es más que una navaja de Ockham matemática: si puedes explicar el universo con una sola línea, ¿para qué quieres dos?

Aunque os pueda parecer mentira después de esta entrada tan larga, en realidad no hemos hablado ni la mitad de las cosas que podríamos decir sobre el ACP, ya que hemos pasado de puntillas por la fontanería matemática densa para que nadie saliera huyendo.

Por ejemplo, no hemos mencionado los supuestos que deberían cumplir los datos, como la famosa normalidad, que a los estadísticos les gusta pedir para todo, aunque el ACP sea bastante todoterreno. Tampoco hemos hablado de la regla de oro que evita que el sistema haga trampas: para que el ACP funcione, existe una restricción obligatoria que dice que la suma de los cuadrados de los coeficientes (los pesos que les damos a cada variable) debe ser igual a uno.

¿Por qué? Porque si no pusiéramos ese límite, las matemáticas simplemente usarían pesos infinitamente grandes para maximizar la varianza artificialmente y ganar el juego sin aportar información real. Todo un mundo de detalles escabrosos y teoremas capaces de provocar un insomnio grave. Pero esa es otra historia…