Chi-square for goodness of fit.

Chi-square for goodness of fit allows us to infer whether a sample can come from a given population.
How much would not have paid King Solomon to know something more about calculating odds!. And he was quite wise. But surely, if he had had a minimal understanding of statistics, his decisions would have been much easier. And, of course, he almost certainly would not have had to cut children in half. Clear that, in this case, he would not be famous now. Historical characters are like popular festivities: the wilder, the more preferred.
And to show you what I mean I’m going to imagine, as usual, an example so stupid that you will end up wanting to keep reading.
A suppose
Let’s suppose for a delusional moment that I’m a security guard at a giant candy store. Someone tell me that a child has been caught with a bag of candy that has been allegedly stolen from the giant barrel full of candy in the store. The poor kid says he has done nothing wrong and that he has bought the bag at another store but, of course, what could he say?. What could we do?. I know… split the child in half, as would King Solomon.
But anyone immediately realizes that this solution is not a good one. Who knows?, the poor child could be innocent, as he claims. So let’s think a little about how we can find out if the candies come from our shop or from ours competitors.
Chi-square for goodness of fit
The store clerk tell us that in the barrel 25% of the candies are orange flavor, 20% strawberry, 20% mint, 25% coffee and 10% chocolate. So we look into the child’s bag and find out that it has 100 candies of the following flavors: 27 orange, 18 strawberry, 20 mint, 22 coffee and 13 chocolate.
If those candies were from our barrel, the flavor distribution would be the same in both the barrel and the bag. From a practical point of view, we may assume that the robber pulled out 100 random candies from the barrel (we can’t follow this reasoning if he has selected the candies by its flavors).
So the question is simple: does the bag’s distribution of flavors support the candies come from a random sample of our barrel?. Small differences would be due to sampling error, so we state our null hypothesis that the kid has stolen our candy.
First, we think about the theoretical distribution that would have to have the candy and compare it with the distribution they have, always assuming that null hypothesis is true.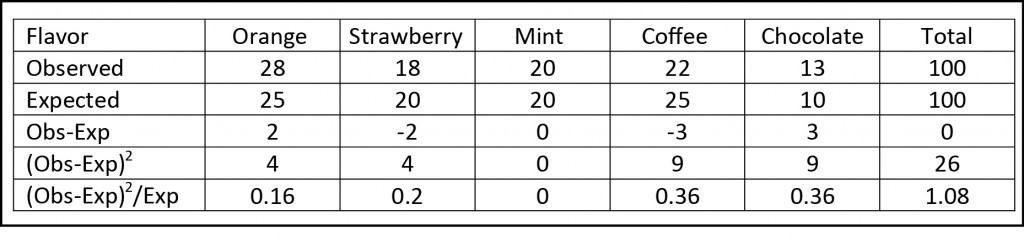
Although the difference equals five in both examples, it seems clear that margin of error is greater in the first case. This is why we standardize the differences dividing them by the expected value. And, finally, we add these results to obtain a certain value, which in our example is 1.08.
And, 1.08 is a lot or a few?. It depends, sometimes it will be a lot and others a few. But we do know that this value approximately follows a chi-square probability distribution with a number of degrees of freedom equal to the number of categories (flavors in our example) minus one.
Know we can calculate the probability of a chi value of 1.08 with four degrees of freedom. We can use a computer program, a table of probabilities or one of the available calculators on the Internet. We come up with a p value of 0.89 (89%). As is greater than 5%, we cannot reject the null hypothesis, so we conclude that the child is not only a thief, but also a liar. His bag of candy is representative of a random sample obtained from our barrel.
We’re leaving…
You have seen how easy it is to check the origin of a sample by applying the chi-square test. But this test is not only good for studying the origin of a random sample. It can also be used to check if there is any dependence among qualitative variables. But that’s another story…
