Kappa coefficient of interobserver agreement.

When we have measurements obtained by two observers, the kappa coefficient allows us to separate the degree of coincidence due to chance.
We all know that the less we go to the doctor, the best. And this is so for two reasons. First, because if we go to many doctors we are either physically ill or very mentally sick (some unfortunates are both of them). And second, which is the fact I am always struck by, because every doctor tells you something different. And it’s not that doctors don’t know their job, it’s that getting an agreement is not as simple as it seems.
To give you an idea, the problem starts when wanting to know if two doctor who assess the same diagnostic test have a good degree of agreement. Let’s see an example.
The director’s problem
Imagine for a moment than I am the manager of a hospital and I want to hire a pathologist because the only one that works at the hospital is overworked.
I meet with my pathologist and the applicant and give them 795 biopsies to tell me if there’re malignant cells in them. As you can see in the first table, my pathologist finds malignant cells in 99 biopsies, while the applicant sees them in 135 (do not panic, in real life difference couldn’t be so wide, could be?).
We wonder what degree of agreement or, rather, concordance exists between the two. The first think that comes to our mind is to calculate the number of biopsies in which they agree: they both agree with 637 normal biopsies and 76 with malignant cells, so the percentages of cases of agreement can be calculated as (637+76)/795=0.896. Hurray!, we think, the two agree almost 90% of the time. The result is not as bad as it seemed to be looking at the table.
But it turns out that when I’m about to hire the new pathologist I wonder if they could have agreed just by chance.
So, a stupid experiment springs to my mind: I take the 795 biopsies and throw a coin, labeling each biopsy as normal if I get heads, or pathological, if tails.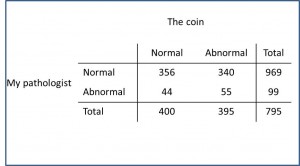
The coin says I have 400 normal biopsies and 395 with malignant cells. If I calculate the concordance between the coin and the pathologist, I see that it values (365+55)/795=0.516, 52%!. This is really amazing, just by chance there’s agreement in half of the cases (yes, yes, I know that those know-it-all of you will be thinking that it’s not a surprise, since 50% is the probability of each possible outcome when tossing a coin).
o I start thinking how to save money for my hospital and I come out with another experiment that this time is not only stupid, but totally ridiculous: I offer my cousin to do the test instead of throwing a coin (by this time I’m going to left my brother-in-law alone).
The problem, of course, is that my cousin is not a doctor and, although a nice guy, pathology is not his main topic. So, when he starts to see the colorful cells he thinks it’s impossible that such beauty is produced by malignant cells and gives all the biopsies as normal.
hen we look at the table with the results the first think that we think if to burn it but, for the sake of curiosity, we calculate the concordance between my cousin and my pathologist and see that it’s 696/795=0.875, 87!. Conclusion: it could be more convenient to me to hire my cousin instead of a new pathologist.
At this stage many of you will think that I forgot to take my medication this morning, but the truth is that all these examples serve to show you that, if we want to know what the agreement between two observers is, we must first get rid of the cumbersome and everlasting effect of chance. And for that, mathematicians have invented a statistic called kappa, the interobserver agreement coefficient.
The concept of concordance
The function of kappa is to exclude from the observed agreement that part that is due to chance, obtaining a more representative measure of the strength of agreement between observers. Its formula is a ratio in which the numerator is the difference between observed and random difference and which denominator represents the complementary of the random agreement: (Po-Pr) / (1-Pr).
We already know the value of Po with two pathologists: 0.89. To get Pr we have to calculate the theoretical expected values for each cell of the table, in a similar way that we remember we did with chi squared test: the expected value of each cell is the product of the total of its row and column divided by the total of the table. As an example, the expected value of the first cell of our table is (696×660)/795=578. With the expected values we can calculate the probability of agreement due to chance using the same method we used earlier with observed values: (578+17)/795=0.74.
Kappa coefficient
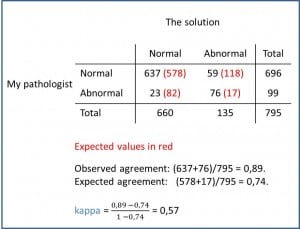
Values greater than 0 indicate that concordance is slight (0.01-0.20), fair (0.21-0.40), moderate (0.41-0.60), substantial (0.61-0.80) or almost perfect (0.81-1.00). In our case, there’s a fairly good agreement between the two pathologists. If you are curious, you can calculate the kappa for my cousin and you’ll see that it’s no better than flipping a coin.
Kappa can also be calculated if we have measurements of several observers and more than one result for each observation, but tables get so unfriendly that it is better to use a statistical program to calculate it, and by the way, come up with confidence intervals.
Anyway, do not put much trust in kappa, because it needs not to be greater difference among table’s cells. If a cell has few cases the coefficient will tend to underestimate the actual concordance even if it’s very good.
We’re leaving…
Finally, say that, although all our examples showed tests with dichotomous result, it’s also possible to calculate interobserver agreement with quantitative results (a rating scale, for instance). Of course, for that we have to use another statistical technique as Bland-Altman’s test, but that’s another story…
