NNT’s confidence interval.

The calculation and interpretation of the confidence intervals of the number needed to treat are described, including the negative extremes of the interval.</p
The number needed to treat (NNT) is an impact measure that tells us in a simple way about the effectiveness of an intervention or its side effects. If the treatment tries to avoid unpleasant events, the NNT will show us an appreciation of the patients that we have to submit to treatment to avoid one of these events. In this case we talk about NNTB, the number to deal with to benefit.
In other cases, the intervention may produce adverse effects. Then we will talk about the NNTH or number to try to harm one (produce an unpleasant event).
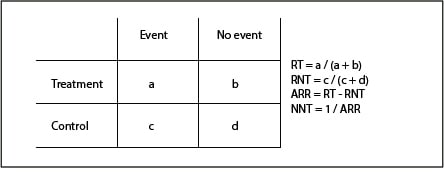
The calculation of the NNT is simple when we have a contingency table like the one we see in the first table. It is usually calculated as the inverse of the absolute risk reduction (1 / ARR) and is given as a point estimate value. The problem is that this ignores the probabilistic nature of the NNT, so the most correct would be to specify its 95% confidence interval (95CI), as we do with the rest of the measures.
We already know that the 95CI of any measure responds to the following formula:
95CI (X) = X ± (1.96 x SE (X)), where SE is the standard error.
Thus the lower and upper limits of the interval would be the following:
X – 1.96 SE (X), X + 1.96 SE (X)
The tribulations of NNT’s confidence interval
And here we have a problem with the NNT’s 95CI. This interval cannot be calculated directly because NNT does not have a normal distribution. Therefore, some tricks have been invented to calculate it, such us to calculate the 95CI of the ARR and use its limits to calculate the NNT’s, as follows:
95CI (ARR) = ARR – 1,96(SE(ARR)) , ARR + 1,96(SE(ARR))
CI(NNT) = 1 / upper limit of the 95CI (ARR), 1 / lower limit of the 95CI (ARR) (we use the upper limit of the ARR to calculate the lower limit of the NNT, and vice versa, because being the treatment beneficial, risk reduction would in fact be a negative value [RT – RNT], although we usually speak of it in absolute value).
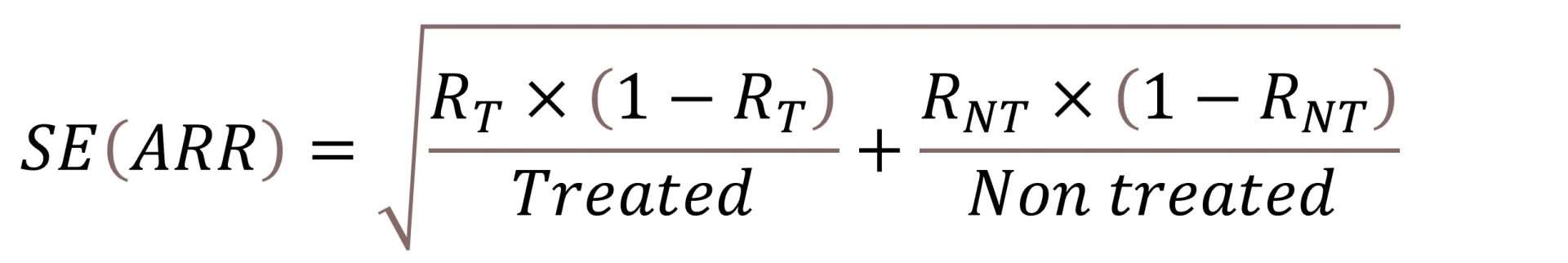

We just need to know how to calculate the RAR’s SE, which turns out to be done with a slightly unfriendly formula that I put to you just in case anyone is curious to see it:In the second table you can see a numerical example to calculate the NNT and its interval. You see that the NNT = 25, with an 95CI of 15 to 71. Look at the asymmetry of the interval since, as we have said, does not follow a normal distribution. In addition, far from the fixed value of 25, the interval values say that in the best case we will have to treat 15 patients to avoid an adverse effect, but in the worst case this value can rise to 71.
To all the above difficulty for its calculation, another added difficulty arises when the ARR’s 95CI includes zero. In general, the lower the effect of the treatment (the lower the ARR) the higher the NNT (it will be necessary to treat more to avoid an unpleasant event), so in the extreme value of the effect is zero, the NNT’s value will be infinite (an infinite number of patients would have to be treated to avoid an unpleasant event).
So it is easy to imagine that if the 95CI of the ARR includes zero, the 95CI of the NNT will include infinity. It will be a discontinuous interval with a negative value limit and a positive one, which can pose problems for its interpretation.
For example, suppose we have a trial in which we calculated an ARR of 0.01 with a 95CI of -0.01 to 0.03. With the absolute value we have no problem, the NNT is 100 but, what about with the interval? For it would go from -100 to 33, going through infinity (actually, from minus infinity to -100 and from 33 to infinity).
How do we interpret a negative NNT? In this case, as we have already said, we are dealing with an NNTB, so its negative value can be interpreted as a positive value of its alter ego, the NNTH. In our example, -100 would mean that we will have an adverse effect for every 100 treated. In short, our interval would tell us that we could produce one event for every 100 treated, in the worst case, or avoid one for every 33 treated, in the best. This ensures that the interval is continuous and includes the point estimate, but it will have little application as a practical measure. Basically, it may make little sense to calculate the NNT when the ARR is not significant (its 95CI includes zero).
We’re leaving…
At this point, the head begins to smoke us out, so let’s go ending today. Needless to say, everything I have explained about the calculation of the interval can be done clicking with any of the calculators available on the Internet, so we will not have to do any math.
In addition, although the NNT calculation is simple when we have a contingency table, we often have adjusted risk values obtained from regression models. Then, the maths for the calculation of the NNT and its interval gets a little complicated. But that is another story…

[…] https://www. cienciasinseso. com/en/nnts-confidence-interval/ […]