The p-curve.

I’m sure you all know the urban legend of the vanishing hitchhiker. In Spain, we call her the girl on the curve. It is the chilling story of the mysterious young woman who appears on the darkest nights at a dangerous curve in the road. An unsuspecting driver, a late brake and, bam!, there she is, with her white dress and her ghostly expression.

But what if I told you that the world of science has its own “curve girl”? No, I’m not talking about a spectrum wandering through dark laboratories, but about something equally intriguing: the p-curve, which is formed by the significance values ​​of the primary studies of a meta-analysis. Yes, those seemingly innocuous numbers, which indicate statistical significance, can hide mysteries and surprises.

Like the girl who appears on the curve, the p-values ​​can reveal to us whether we are dealing with an authentic or casual discovery and, even, whether something more sinister is hidden behind these data, which may have been tortured without mercy.

In fact, looking at the shape of the p-curve can be as revealing as coming face to face with the legendary girl. Are we seeing a true effect, is it a spurious effect, or perhaps the data have been manipulated to force a statistically significant conclusion?

If you continue reading, we will see how our girl can help us detect deception and search for the truth, just as a driver must pay attention to the signs on the road to avoid an unexpected encounter with the unknown. So buckle up and prepare for a fascinating journey down the winding roads of meta-analysis.

The uncertainty of meta-analysis

Its defenders staunchly affirm that meta-analysis is a powerful and essential tool in the world of scientific research. By combining results from multiple studies, it allows us to increase statistical power, identify patterns and subgroups, and improve the precision of estimates, enabling greater efficiency in decision-making.

All of this would be the case in an ideal world, in which meta-analyses, their primary studies, and the people who carry them out were, in turn, perfect and honest. And this, unfortunately, is often far from reality.

There are at least three major enemies of meta-analysis as a quantitative synthesis method that can bias its results. Let’s see them.

Publication bias

Logically, for the conclusions of a meta-analysis to be valid, it must include all the available evidence on the topic, which may not happen if we do not find any of the studies (retrieval bias) or if not all the studies on the topic that have been done have been published (publication bias).

We saw in a previous post that a study may not be published for various reasons, although the first thing that comes to mind is the problem of small studies.

In principle, studies with smaller sample sizes are more at risk of not being published, unless they detect a large effect size. These tend to be the ones with a larger standard error and, therefore, a more imprecise effect estimates.

But, the truth is that there is a more important factor than the size of the effect on the risk of not being published, and this is none other than the value of statistical significance of the effect measured in the study, the p-value. In this world prostrated at the feet of this arbitrary goddess whose meaning is poorly understood by many, it is very likely that a study that does not have a p < 0.05 will end up archived forever on the researcher’s computer disk.

This explains why studies with negative and non-significant results tend to disappear. In reality, it is related, although indirectly, to the sample size of the studies: the smaller ones will have less power, so they will only reach values ​​of p < 0.05 when the magnitude of the effect they detect is large.

Chance, our inseparable partner

When performing a hypothesis test we establish a null hypothesis and look for the level of statistical significance, the p-value.

If p < 0.05, we reject (by convention) the null hypothesis, which usually leads us to accept the effect we observe as real. The problem is that we always run the risk of making a type 1 error and detecting a false positive.

This also occurs when we look at the p-values ​​of the studies in a meta-analysis: on average, in 1 in 20 studies we can actually find a false positive.

If you torture the data enough, the will end up confessing

We have already seen the cult of p. Studies are carried out by so-called human beings, who always want fame and prestige, if not money, so they are usually pressured to obtain the desired p < 0.05. The consequence is the practice of p-hacking, that can be undertaken with manipulation and bias of the data, torturing them mercilessly until they end up confessing a statistically significant p-value.

To try to avoid all these inconveniences, we can resort to our girl and her curve, the so-called p-curve. This technique focuses only on the significant p-values ​​of the primary studies in the meta-analysis and allows us to estimate, in addition to publication bias, whether there may be a real effect after our study, what the magnitude is, and whether there is suspicion of bad practices due to part of the researchers to obtain statistically significant values.

And all of this without the need to blame everything on studies with smaller sample sizes. Let’s go with the p-curve.

The p-curve

The p-curve, as its name suggests, is based on the shape of the curve of the p-values ​​of the effect estimates from primary studies, but only from those that are less than 0.05. Actually, rather than a curve, it is a histogram of p-values, the shape of which is supposed to depend on the sample size of the studies and, more importantly, on whether there is a real effect behind our data.

To better understand how it works, we are going to do a simulation with completely invented data that we will never encounter in our practice. We are going to simulate several meta-analyses with 5000 primary studies, in which we are going to vary the sample size of the primary studies (n = 20, 50 and 80) and the real effect that we want to detect (θ = 0, 0.3 and 0.5). Finally, we assume that all studies try to assume the same population effect or, in other words, a fixed effect model.

Once the data is obtained, we draw the histograms with the frequency of the p value < 0.05.

In the first figure we see the histograms for the three sample sizes when there is no effect in the population (for example, a standardized mean difference). In this case, θ = 0.

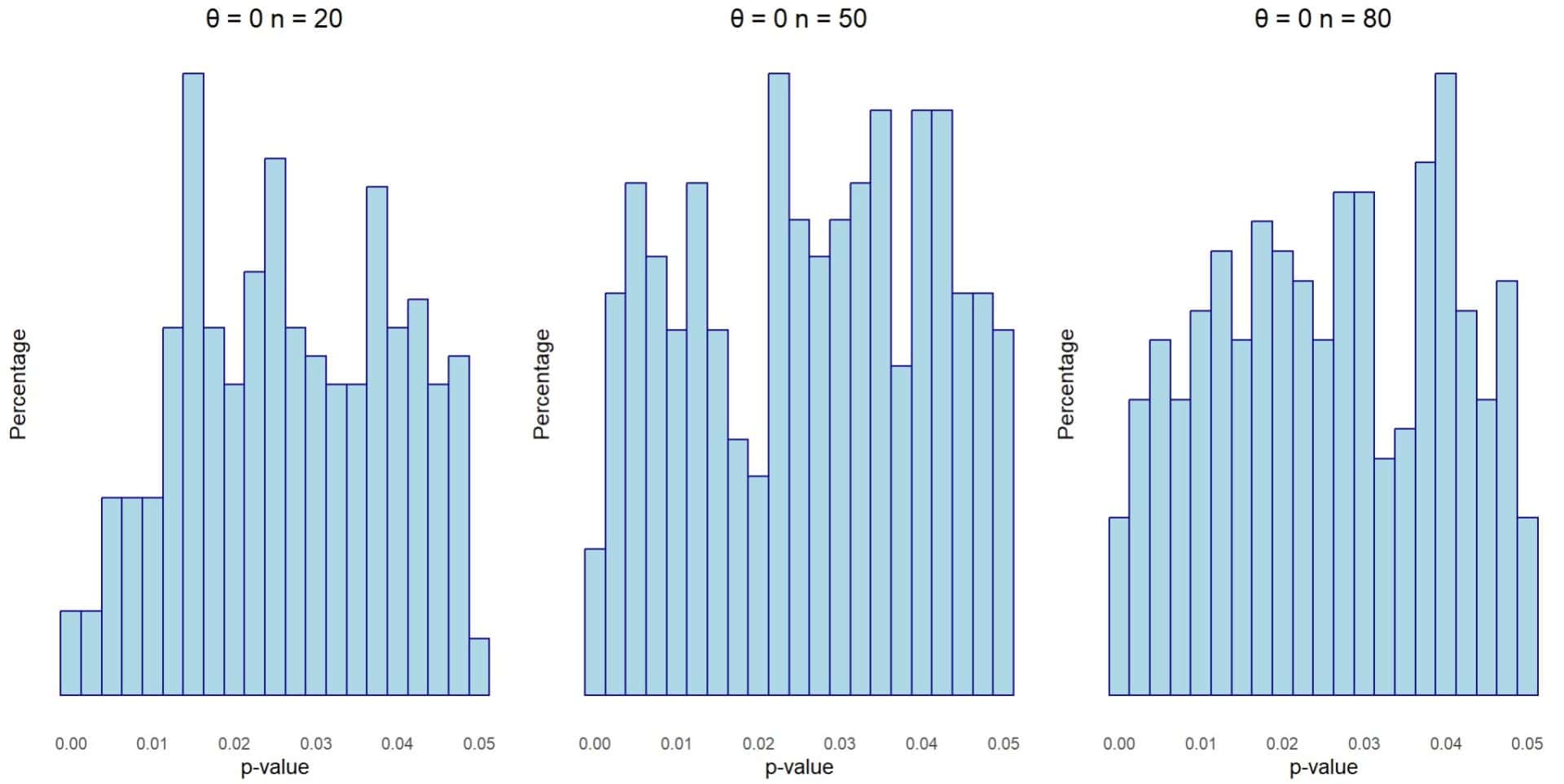
We see that, although there is no real effect in the population (this time we know it because we have generated the data, but it is an unknown data that we will want to estimate), we obtain a value of p < 0.05 in many studies. We are not surprised, it is the type 1 error coming into play: 1 in 20 contrasts, on average, will be falsely positive, so we can expect 250 of the 5000 studies to detect a significant effect just by chance.

Of course, it will be just as likely to find values ​​of p = 0.04 as p = 0.01 or any other value, so the values ​​follow a uniform distribution. Furthermore, this distribution does not change when the sample size (and, therefore, the power) of the primary studies increases. If the effect we want to estimate in the population is 0, p-values ​​will be uniformly distributed, regardless of the sample size of the studies.

When the p-curve shows this aspect, we can suspect that there is no population effect and that the observed findings are spurious, due to chance. This is the type of curve when the null hypothesis (θ = 0) is true.

Let’s now look at the second figure. Here we make the same variations with the sample sizes, but we assume that there is a real effect in the population, with θ = 0.3 and 0.5.

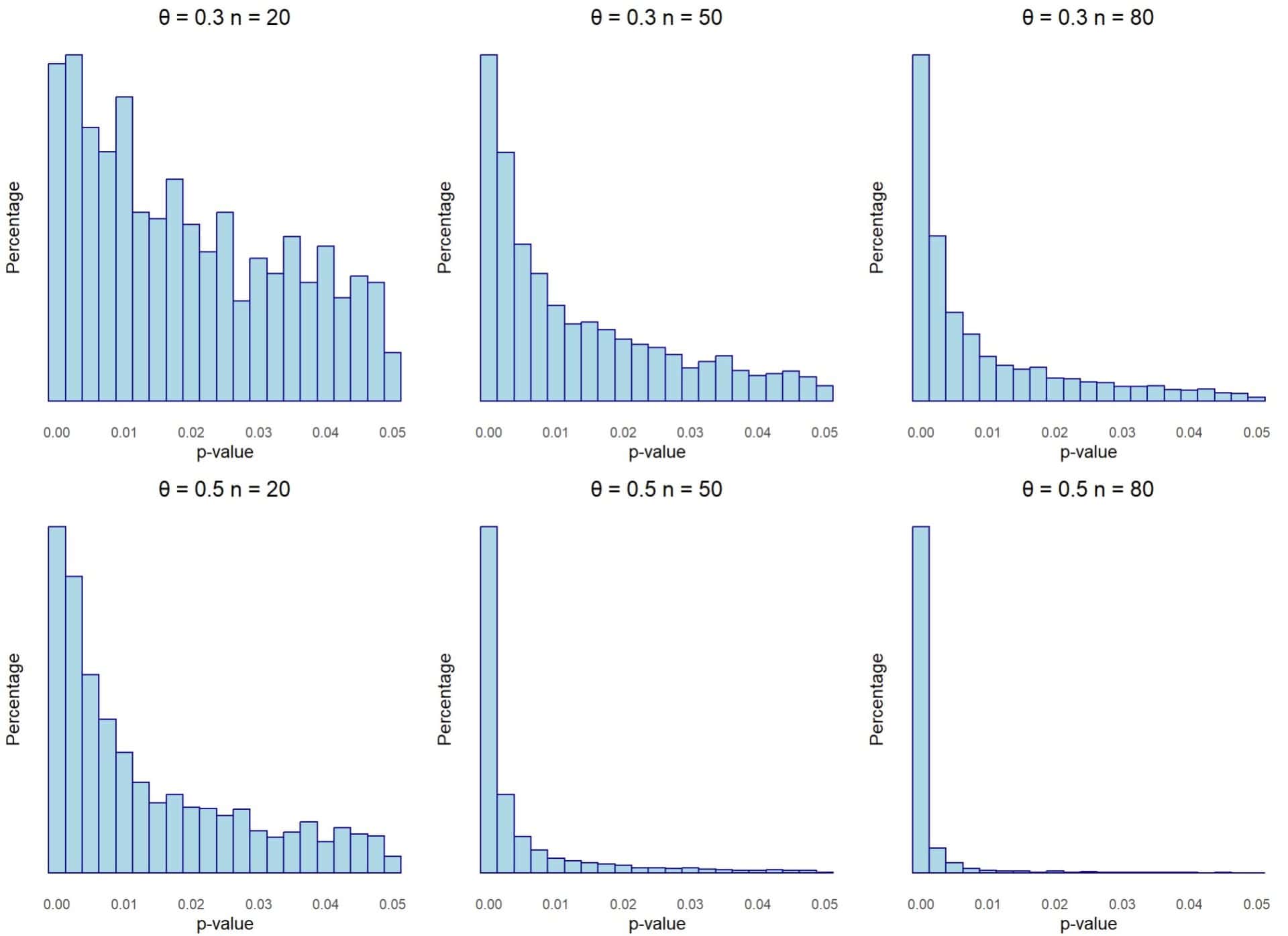
When the null hypothesis is false and there is a real effect behind our data, the shape of the p-curve changes drastically. Now it is more likely to obtain lower p-values ​​(for example, p = 0.01) than those that show marginal significance (for example, p = 0.045), so the values ​​accumulate to the left and the curve has a bias to the right.

This bias will be greater the larger the real effect and the greater power the primary studies have to detect the effect (the larger their sample size). We can see this by comparing the six histograms.

In summary, we may suspect that our data reflect a real effect when the p-curve is skewed to the right. And what happens when the data has been tortured? Let’s think a little and we will understand how the shape of the curve would be modified.

Usually, the data can be manipulated to obtain statistical significance when the value obtained is close to p = 0.05. If it is too far away, it will be difficult to achieve the desired p < 0.05. But if it is close, you can make subgroups, removing data with some excuse, moving others from here to there, etc., until the p-value falls below the threshold and the desired significance is obtained.

In this case, p = 0.049 will suffice, so efforts to change the result will end when the threshold of p = 0.05 is crossed. For this reason, the significant p-values ​​accumulate to the right of the graph, so we will see a p-curve skewed to the left. If we see this, it will smell like singeing.

In theory, it is possible for the torturer to try hard enough to lower the p-value further, but it is unlikely (although theoretically possible) that he will achieve a right-skewed curve. Even the most sophisticated means of torture have their limits.

And now that we understand the concept, let’s see how we can quantify it, using two methods: the test for right bias and the test for a flat curve, also called the 33% power test.

Test for right bias

We can measure the right skew of the curve in two ways. The first, and simplest, is to use the binomial probability distribution.

If we split the horizontal axis of the histogram into two halves (at p = 0.025), we can expect that there will be a greater number of values ​​in the left half when there is a real effect and the curve is skewed to the right.

Let’s assume that we have a meta-analysis with 30 studies with p < 0.05, of which 21 have p < 0.025. Assuming that, under the null hypothesis of equality, there are equal numbers in both halves (p = 0.5), we can calculate the probability of finding 21 or more with values ​​of p < 0.025. If you want, you can write the following command in R:

binom.test(21, 30, 0.5, alternative = "greater")$p.value

It gives us a result of p = 0.021, so we reject the null hypothesis and conclude that there is a bias to the right.

The second, slightly more complex way to do this test is to calculate the probability of obtaining each value of p or lower (a cumulative probability called the pp-value) and apply Fisher’s method.

Suppose we have 5 values ​​of p < 0.05: 0.01, 0.02, 0.02, 0.04 and 0.015. Under the assumption of the null hypothesis, these values ​​follow a uniform distribution, so we can calculate the cumulative probabilities (pp-values), multiplying the values ​​by 20 (which is the same as projecting them on the segment [0, 1] in which distribute the probabilities): 0.2, 0.4, 0.4, 0.8 and 0.3.

Now we calculate the logarithms of the pp-values, add them and multiply them by -2, obtaining the test statistic, which follows a chi-square distribution with 2k degrees of freedom, k being the number of pp-values. I have calculated it and its value is 9.74.

If I compute the probability of obtaining a statistic value like this or higher, it is 0.46, so I cannot reject the null hypothesis, which says that the significant p-values ​​follow a uniform distribution and that the findings found are probably due to random.

Test for flat curve

In the previous example we could not reject the null hypothesis. This may be due to two reasons. First, maybe there is no real effect behind our data. Second, it is possible that the studies do not have enough power to generate a chi-square statistic that reaches statistical significance. When this happens to us, we can try to reject the null hypothesis by empirically demonstrating that our p-curve is NOT flat.

In this case, we change the approach of the null hypothesis, which will now state that our curve is not flat, but rather has a small bias to the right, since the data hides an effect of not very large magnitude (otherwise, it would have be detected with the previous method).

This method is based on calculating pp-values ​​assuming that the effect is small. How small? By convention, and arbitrarily, that it can be detected if the power of the studies is 33%.

The calculation of these pp-values ​​is complex and involves using non-central probability distributions, which we are not going to go into now. Once calculated, we will proceed the same as with the previous method, but with the difference that we will have little interest in rejecting the null hypothesis, since this would imply rejecting the idea that there is a real effect, even if it is of small magnitude.

We are leaving…

I don’t know about you, but I’m a little dizzy with so many curves, so we’re going to take the exit straight line.

We have seen how some of the problems of meta-analysis are based on assumptions that are often just that, assumptions, such as the clear and direct relationship between publication bias and the size of studies that are not published.

Furthermore, we have discovered a new tool that allows us to try to suspect whether we may be dealing with real effects or spurious findings, simple false positives due to chance and the methodology with which the hypothesis tests are carried out.

As if that were not enough, these methods can make us suspect that there may have been manipulation of the data to achieve statistical significance, so the reliability of the results of the meta-analysis will lose its value.

As I always tell you, the important thing is to understand the concept and not try to do these tests by hand. All the methods we have seen can be done with statistical packages or with calculators available on the Internet.

I told you at the beginning that the p curve can also be used, not only to suspect the existence of a real effect, but to estimate its magnitude. This implies somewhat more complex methods and the use of the non-central probability distributions that we have mentioned in passing and that represent the distribution of the data when the true hypothesis is the alternative and not the null hypothesis. But that is another story…