Critical appraisal of meta-analysis of diagnostic accuracy.

Meta-analysis of diagnostic accuracy’s methodology, its most characteristic biases and parameters, and the basis for its critical appraisal are described.
The genius that I am talking about in the title of this post is none other than Alan Mathison Turing, considered one of the fathers of computer science and a forerunner of modern computing.
For mathematicians, Turing is best known for his involvement in the solution of the decision problem previously proposed by Gottfried Wilhelm Leibniz and David Hilbert, who were seeking to define a method that could be applied to any mathematical sentence to prove whether that sentence were or not true (to those interested in the matter, it could be demonstrated that such a method does not exist).
But what it is Turing is famous for among the general public comes thanks to the cinema and to his work in statistics during World War II. And it is that Turing was taken to exploiting Bayesian magic to deepen the concept of how the evidence we are collecting during an investigation can support the initial hypothesis or not, thus favoring the development of a new alternative hypothesis. This allowed him to decipher the code of the Enigma machine, which was the one used by the German navy’s sailors to encrypt their messages, and that is the story that has been taken to the screen.
This line of work led to the development of concepts such as the weight of evidence and concepts of probability, with which confront null and alternative hypotheses, which were applied in biomedicine and enabled the development of new ways to evaluate new diagnostic tests capabilities, such as the ones we are going to deal with today.
But all this story about Alan Turing turn out to be just a recognition of one of the people whose contribution made it possible to develop the methodological design that we are going to talk about today, which is none other than the meta-analysis of diagnostic accuracy.
We already know that a meta-analysis is a quantitative synthesis method that is used in systematic reviews to integrate the results of primary studies into a summary result measure. The most common is to find systematic reviews on treatment, for which the implementation methodology and the choice of summary result measure are quite well defined. Reviews on diagnostic tests, which have been possible after the development and characterization of the parameters that measure the diagnostic performance of a test, are less common.
The process of conducting a diagnostic systematic review essentially follows the same guidelines as a treatment review, although there are some specific differences that we will try to clarify. We will focus first on the choice of the outcome summary measure and try to take into account the rest of the peculiarities when we give some recommendations for a critical appraisal of these studies.
Characteristics of meta-analysis of diagnostic accuracy
When choosing the outcome measure, we will find the first big difference with the meta-analyzes of treatment. In the meta-analysis of diagnostic accuracy (MDA) the most frequent way to assess the test is to combine sensitivity and specificity as summary values. However, these indicators present the problem that the cut-off points to consider the results of the test as positive or negative usually vary among the different primary studies of the review. Moreover, in some cases positivity may depend on the objectivity of the evaluator (think of results of imaging tests).
All this, besides being a source of heterogeneity among the primary studies, constitutes the origin of a typical MDA bias called the threshold effect, in which we will stop a little later.
For this reason, many authors do not like to use sensitivity and specificity as summary measures and resort to positive and negative likelihood ratios. These ratios have two advantages. First, they are more robust against the presence of threshold effect. Second, as we know, they allow calculating the post-test probability either using Bayes’ rule (pre-test odds x likelihood ratio = posttest odds) or a Fagan’s nomogram (you can review these concepts in the corresponding post).
Finally, a third possibility is to resort to another of the inventions that derive from Turing’s work: the diagnostic odds ratio (DOR).
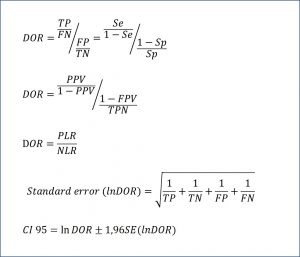
The odds of the patient being positive versus being negative is only the ratio between true positives (TP) and false negatives (FN): TP / FN. On the other hand, the odds of the healthy being positive versus negative is the quotient between false positives (FP) and true negatives (TN): FP / TN. And seeing this, we can only define the ratio between the two odds, as you can see in the attached figure. The DOR can also be expressed in terms of the predictive values and the likelihood ratios, according to the expressions that you can see in the same figure. Finally, it is also possible to calculate their confidence interval, according to the formula that ends the figure.
Like all odds ratios, the possible values of the DOR go from zero to infinity. The null value is 1, which means that the test has no discriminatory capacity between the healthy and the sick. A value greater than one indicates discriminatory capacity, which will be greater the greater the value. Finally, values between zero and 1 will indicate that the test not only does not discriminate well between the sick and healthy, but classifies them in a wrong way and gives us more negative values among the sick than among the healthy.
The DOR is a global parameter easy to interpret and does not depend on the prevalence of the disease, although it must be said that it can vary between groups of patients with different severity of disease. In addition, it is also a very robust measure against the threshold effect and is very useful for calculating the summary ROC curves that we will comment on below.
The second peculiar aspect of MDA that we are going to deal with is the threshold effect. We must always assess their presence when we find ourselves before a MDA. The first thing will be to observe the clinical heterogeneity among the primary studies, which could be evident without needing to make many considerations. There is also a simple mathematical form, which is to calculate the Spearman’s correlation coefficient between sensitivity and specificity . If there is a threshold effect, there will be an inverse correlation between the two, the stronger the higher the threshold effect.
Finally, a graphical method is to assess the dispersion of the sensitivity and specificity representation of the primary studies on the summary ROC curve of the meta-analysis. A dispersion allows us to suspect the threshold effect, but it can also occur due to the heterogeneity of the studies and other biases such as selection’s or verification’s.
The third specific element of MDA that we are going to comment on is that of the summary ROC curve (sROC), which is an estimate of the common ROC curve adjusted according to the results of the primary studies of the review. There are several ways to calculate it, some quite complicated from the mathematical point of view, but the most used are the regression models that use the DOR as an estimator, since, as we have said, it is very robust against heterogeneity and the threshold effect. But do not be alarmed, most of the statistical packages calculate and represent the sROC with little effort.
The reading of sROC is similar to that of any ROC curve. The two more used parameters are area under the ROC curve (AUC) and Q index. The AUC of a perfect curve is equal to 1. Values above 0.5 indicate its discriminatory diagnostic capacity, which will be higher the closer it gets to 1. A value of 0.5 tells us that the usefulness of the test is the same that flipping a coin. Finally, values below 0.5 indicate that the test does not contribute at all to the diagnosis it intends to perform.
On the other hand, the Q index corresponds to the point at which sensitivity and specificity are equal. Similar to AUC manner, a value greater than 0.5 indicate the overall effectiveness of the diagnostic test, which will be higher the closer the index value is to 1. In addition, confidence intervals can also be calculated both for AUC as Q index, with which it will be possible to assess the precision of the estimation of the summary measure of the MDA.
Critical appraisal of meta-analysis of diagnostic accuracy
Once seen (at a glance) the specific aspects of MDA, we will give some recommendations to perform the critical appraising of this type of study. CASP network does not provide a specific tool for MDA, but we can follow the lines of the systematic review of treatment studies taking into account the differential aspects of MDA. As always, we will follow our three basic pillars: validity, relevance and applicability.
Let’s start with the questions that value the VALIDITY of the study.
The first question asks if it has been clearly specified the issue of the review. As with any systematic review, diagnostic tests’ should try to answer a specific question that is clinically relevant, and which is usually proposed following the PICO scheme of a structured clinical question. The second question makes us reflect if the type of studies that have been included in the review are adequate. The ideal design is that of a cohort to which the diagnostic test that we want to assess and the gold standard are blindly and independently applied. Other studies based on case-control designs are less valid for the evaluation of diagnostic tests, and will reduce the validity of the results.
If the answer to both questions is yes, we turn to the secondary criteria. Have important studies that have to do with the subject been included? We must verify that a global and unbiased search of the literature has been carried out. The methodology of the search is similar to that of systematic reviews on treatment, although we should take some precautions. For example, diagnostic studies are usually indexed differently in databases, so the use of the usual filters of other types of revisions can cause us to lose relevant studies. We will have to carefully check the search strategy, which must be provided by the authors of the review.
In addition, we must verify that the authors have ruled out the possibility of a publication bias. This poses a special problem in MDA, since the study of the publication bias in these studies is not well developed and the usual methods such as the funnel plot or the Egger’s test are not very reliable. The most conservative thing to do is always assume that there may be a publication bias.
It is very important that enough has been done to assess the quality of the studies, looking for the existence of possible biases. For this the authors can use specific tools, such as the one provided by the QUADAS-2 declaration.
To finish the section of internal or methodological validity, we must ask ourselves if it was reasonable to combine the results of the primary studies. It is fundamental, in order to draw conclusions from combined data, that studies are homogeneous and that the differences among them are due solely to chance. We will have to assess the possible sources of heterogeneity and if there may be a threshold effect, which the authors have had to take into account.
In summary, the fundamental aspects that we will have to analyze to assess the validity of a MDA will be: 1) that the objectives are well defined; 2) that the bibliographic search has been exhaustive; and 3) that the internal or methodological validity of the included studies has also been verified. In addition, we will review the methodological aspects of the meta-analysis technique: the convenience of combining the studies to perform a quantitative synthesis, an adequate evaluation of the heterogeneity of the primary studies and the possible threshold effect and use of an adequate mathematical model to combine the results of the primary studies (sROC, DOR, etc.).
Regarding the RELEVANCE of the results we must consider what is the overall result of the review and if the interpretation has been made in a judicious manner. We will value more those MDA that provide more robust measures against possible biases, such as likelihood ratios and DOR. In addition, we must assess the accuracy of the results, for which we will use our beloved confidence intervals, which will give us an idea of the precision of the estimation of the true magnitude of the effect in the population.
We’re leaving…
We will conclude the critical appraisal of MDA assessing the APPLICABILITY of the results to our environment. We will have to ask whether we can apply the results to our patients and how they will influence the attention to them. We will have to see if the primary studies of the review describe the participants and if they resemble our patients. In addition, it will be necessary to see if all the relevant results have been considered for decision making in the problem under study and, as always, the benefit-cost-risk ratio must be assessed. The fact that the conclusion of the review seems valid does not mean that we have to apply it in a compulsory way.
Well, with all that said, we are going to finish today. The title of this post refers to the mistreatment suffered by a genius. We already know what genius we were referring to: Alan Turing. Now, we will clarify the abuse. Despite being one of the most brilliant minds of the 20th century, as witnessed by his work on statistics, computing, cryptography, cybernetics, etc., and having saved his country from the blockade of the German Navy during the war, in 1952 he was tried for his homosexuality and convicted of serious indecency and sexual perversion.
As it is easy to understand, his career ended after the trial and Alan Turing died in 1954, apparently after eating a piece of an apple poisoned with cyanide, which was labeled as suicide, although there are theories that speak rather of murder. They say that from here comes the bitten apple of a well-known brand of computers, although there are others who say that the apple just represents a play on words between bite and byte.
I do not know which of the two theories is true, but I prefer to recall Turing every time I see the little-apple. My humble tribute to a great man.
And now we finish. We have seen the peculiarities of the meta-analyzes of diagnostic accuracy and how to assess them. Much more could be said of all the mathematics associated with its specific aspects such as the presentation of variables, the study of publication bias, the threshold effect, etc. But that’s another story…
