Sampling techniques.

The characteristics of the sampling and the main sampling techniques, both probabilistic and non-probabilistic, are described.
Life is full of important decisions. We decided what to study. Sometimes, very few, we can decide where to work. We decided if we marry and to whom (or so we think). We decide where to live, what car to buy, etc. And we’re screwed more times that we’d wish. Don’t you think so?. Then explain to me the meaning of that lament that is heard so often and which states: “if you lived twice …”. That’s it.
So, before making a decision we have to carefully weigh the alternatives available to us. And this truth for most aspects of normal life, applies also to the scientific method, with the added advantage that it tends to be more clearly established what may be the right choice.
And speaking of choice, suppose we want to get an idea of what will be the result of the next election. The way to get the most nearly figures would be to ask all voters for their voting intentions, but anybody can see that this may be impossible from a practical point of view. Consider a large country with fifty million voters. In these cases what we do is to choose a subset of the population, which we call a sample, do the survey among its components and estimate the result in the general population.
Sampling accuracy and precision
But we can ask ourselves, is this estimate reliable?. And the answer is yes, provided that we use a valid sampling technique that allows us to obtain a representative sample of the population. Everything depends on two characteristics of the sampling: accuracy and precision.
The accuracy determines how close the result we obtain in the sample and the inaccessible real value in the population are to each other, and depends on the type of sample chosen. To be exact, the sample must be representative, which means that the distribution of the study variable (and the related variables) must be similar to that of the population.
We usually begins by defining the sampling frame, which is the listing or way of identifying individuals in the population that can access, called sampling units, and on which the selection process will apply. Consider, for example, a population census, a list of medical records, etc. The choice of the frame should be done very carefully because it will determine the interpretation of results.
On the other hand, the accuracy depends on the sample size and the variability among participants, as you surely remember from the formula for calculating confidence intervals (95% CI = 1.96 x value ± standard error).
As the standard error is the quotient of the standard deviation by the square root of the sample size (n), the greater the standard deviation or the smaller the sample size, the greater the confidence interval width and the lower the precision of the estimate. But this is only a half-true that only works if we assume that the population has an infinite size because, in reality, the standard error must be multiplied by a correction factor for finite sample taking into account the population size (N), so the true formula for the confidence interval would be:
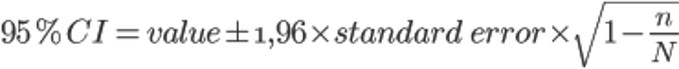
Stop!. Now don’t read faster because I’ve written a formula and turn back to look at it and contemplate, once again, the magic of the central limit theorem, the Sancta Santorum of statistical inference. If the population (N) is large, the ratio quickly becomes almost zero and the error is multiplied almost by one, which practically does not change the interval.
And this is not trivial because it explains why a sample of 1200 voters can estimate the results of, with very little margin for error, both the elections for mayor of New York or those for the US president or the emperor of the entire world, if we had one (provided, of course, that the sample is representative of each electoral census). Moreover, if n is approaching to N, the correction factor approaches to zero and the interval gradually becomes narrower. This explains that if n = N, the value we obtain matches the actual value of the population.
Sampling techniques
Thus, being so the power of an insignificant sample, nobody can be surprised that there are various forms of sampling. First ones that we are going to consider are the probabilistic sampling techniques, in which all subjects have a known, non-zero probability of being selected, although it’s not required that all of them have the same probability. Typically, random selection methods are used to avoid the investigator’s subjectivity and to prevent the possibility that, by chance, the sample is not representative, which could be the origin of random or sampling bias. As always, we cannot get rid of random, by we can quantify it.
Probabilistic sampling
The best known is the simple random sampling, in which each unit in the sampling frame has an equal likelihood of being chosen. The sampling is most often performed without replacement, which means that, once selected, the participant is not remitted back to the population, and so that unit cannot be selected more than once. To make things right, the selection process from the frame is made with a random number table or a computer algorithm.
Sometimes, the variable is not evenly distributed in the population. In these cases, to get a representative sample, we can divide the population into strata and do a random sampling in each stratum. To perform this technique, called stratified random sampling, we need to know the distribution of the variable in the population. Furthermore, the strata should be mutually exclusive, so that the variability within each is minimal and variability between strata is maximized.
If the strata are of similar size, sampling is done proportionally, but if anyone is smaller it can be over represented and include comparatively more sampling units than the rest. The problem is that the analysis is complicated, because you have to weigh the results of each stratum based on their contribution to the overall result, but any statistical program makes these corrections undeterred.
The advantage of this technique is that, provided that data are analyzed correctly, estimates are more accurate, since the overall variance is calculated from the strata, which will always be less than that of the general population. This type of sampling is very useful when the study variable is influenced by other variables of the population. If we consider, for example, the prevalence of ischemic heart disease it may be useful to stratify by sex, weight, age, smoking history, or what we think that can influence the outcome.
A step beyond this approach is the multistage sampling or cluster sampling. In this case the population is divided into primary sampling units which, in turn, are divided into secundary units in which the selection process is conducted. This type, with all the stages we are interested in each case, is widely used in studies about schools, clustering by socioeconomic status, type of education, age, grade or whatever comes to mind. The problem with this design, apart from the complexity of implementation and analysis of results, is that they can be biased if the members of the units are very similar.
hink, for example, we want to study the rate of vaccinations in a city: we divide the city into zones; we randomly select some families in each zone and see how many children are immunized. Logically, if a child is vaccinated surely his brothers will be too, which may overestimate the overall vaccination rate in town if there’re many of these families in the sample from areas with better health status.
Systematic sampling is often used in studies where the sampling frame does not exist or is incomplete. For example, if we want to try an antiinfluenzae drug, we don’t know who are going to get the flu. We choose a constant of randomization (k) and wait quietly for patients arriving to the medical practice. When they have come the first k, we choose one at random and, from there, we included one in k that come with influenza until getting the desired sample size.
Non-probabilistic sampling
In all the above techniques the probability of each members of the population to be selected was known. However, this probability is unknown in non-probabilistic models in which non-random methods are used, so you have to be careful with the representativeness of the sample and the presence of bias.
Consecutive sampling is often used in clinical trials. In the above example about flu, we can enroll the first n who come to the practice and who met the inclusion and exclusion trial’s criteria. Another possibility is the inclusion of volunteers. This is not recommended, since subjects who agree to participate in a study without anyone asking for it may have characteristics that affect the representativeness of the sample.
Marketing specialists very often uses the quota sampling technique, selecting subjects according to the distribution of the variables that interest them, but this type of design is little used in medicine. And finally, let us comment the use of adaptive techniques such as the so-called snowball sampling, random walk sampling or sampling network. For example, think we want to do a study with addicted to illegal substances. It will be difficult to find participants, but when we find the first we may ask if he or she knows of someone else who might participate. This technique, not just invented by me, comes in handy for very hard to reach populations.
We’re leaving…
And with that we ended with techniques that try to get the most suitable type of sample for our study. We would talk about the sample size and how it should be calculate at baseline so that it is neither too big nor too small. But that’s another story…
