Cross-sectional studies.

Cross-sectional studies are observational studies that study more than one variable to determine if there is an association among them.
I hope, for your own good, that you have never had to do with a situation in what you had to pronounce this sentence. And I hope, also for your good, that if you have had to pronounce it, the sentence wouldn’t have begun with the word “darling”. Would it?. Let’s leave it to the conscience of everyone.
What is true is that we have to ask ourselves this question in a much less scabrous situation: when assessing the results of a cross-sectional study. It goes without saying, of course, that in these cases there’s no use for the word “darling”.
Cross-sectional studies
Cross-sectional descriptive studies are a type of observational study in what we extract a sample from the population we want to study and then we measure the frequency of the disease or effect that we are interested in in the individuals of that sample. When we measure more than one variable this studies are called association cross-sectional studies and allow us to determine if there’s any kind of association among the variables.
But these studies have two characteristics that we must always keep in mind. First, they are prevalence studies that measure the frequency at a given time, so the result may vary depending on the timing of measuring the variable. Second, since the measurement is performed simultaneously, it is difficult to establish a cause-effect relationship, something that we all love to do. But it is something we should avoid doing because with this type of study, things are not always what they seem to be. Or rather, things can be a lot more things than what they seem.
What are we talking about?. Let’s consider an example. 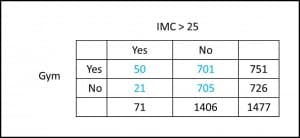
Thus, I make a survey and get data from 1477 individuals approximately my age and ask them if they go to the gym (yes or no) and if they have a body mass index greater than 25 (yes or no). If you look closely at the results depicted in the table you’ll notice that the prevalence of overweight-obesity among those who go to the gym (50/751, about 7%) is higher than among those not going (21/726, about 3%).Oh my goodness!, I think, I not only get tired, but going to the gym I have twice the chance of being fat. Conclusion: I’ll leave the gym tomorrow.
Do you see how easy it is to reach an absurd (rather stupid, in this case) conclusion?. But the data are there, so we have to find an explanation to understand why they suggest something that goes against our common sense. And there are several possible explanations for these results.
The first is that going to the gym actually favors one fattening. It seems unlikely, but you never know … Imagine that working out motivates athletes to eat like wild beasts during the next six hours after a sports session.
The second is that obese going to the gym live longer than those who don’t go. Let’s think that exercise prevents death from cardiovascular disease in obese patients. It would explain why there are more obese (in proportion) in the gym than outside it: obese going to the gym die less that those not going. At the end of the day we are dealing with a prevalence study, so we see the final result at the time of measurement.
Reverse causality
The third possibility is that the disease can influence the frequency of exposure, which is known as reverse causality. In our example, there could be more obese in the gym because the treatment recommendations they receive is doing it: to join a gym. This does not sound as ridiculous as the first one.
But we still have more possible explanations. So far we have tried to explain an association between the two variables that we have assumed as real. But what if the association is not real?. How can we get a false association between the two variables?. Again, we have three possible explanations.
First, our old friend: random. Some of you will tell me that we can calculate statistical significance or confidence intervals, but so what?. Even in the case of statistical significance, it only means that we can rule out the effect of random, but with some degree of uncertainty. Even with p < 0.05, there’s always a chance of committing a type I error, and erroneously reject the effect of chance. We can measure random, but never get rid of it.
Selection bias
The second is that we have committed some kind of bias that invalidates our results. Sometimes the disease’s characteristics can result in a different probability of choosing exposed and unexposed subjects, resulting in a selection bias. Imagine that instead of a survey (by telephone, for example) we have used a medical record.
It may happen that obese going to the gym are more responsible with their health care and go to the doctor more than those that don’t go to the gym. In this situation, it will be more likely that we include obese athletes in the study, making a higher estimate of the true proportion. Sometimes the study factor may be somewhat stigmatizing from the social point of view, so diseased people will have less desire to participate in the study (and recognize their disease) that those who are healthy. In this case, we’ll underestimate the frequency of disease.
Classification bias
In our example, it may be that obese people who do not go to the gym answer to the survey lying about their true weight, which will be wrongly classified. This classification bias can occur randomly in the two groups of exposed and unexposed, thereby favoring the lack of association (the null hypothesis), and so the association will be underestimated, if it exists. The problem is when this error is systematic in one of the two groups, as this can both underestimate and overestimate the association between exposure and disease.
Confounding variable
And finally, the third possibility is that there is a confounding variable that is distributed differently between exposed and unexposed. I can think that those who go to the gym are younger than those who don’t. I t is possible that younger obese are more likely to go to the gym. If we stratified the results by the confounding variable, age, we can determine its influence on the association.
To finish, I only want to apologize to all obese in the world for using them in the example but, for once, I wanted to let the smokers alone.
We’re leaving…
As you can see, things are not always what they seem at first glance, so the results should be interpreted with common sense and in the light of existing knowledge, without falling into the trap of establishing causal relationships from associations detected in observational studies. To stablish cause and effect we always need experimental studies, the paradigm of which is the clinical trial. But that’s another story…
