Correlación lineal.

La correlación lineal representa la fuerza de asociación entre dos variables cuantitativas, sin implicar dependencia ni causalidad.
Sabemos ya de la relación entre variables. ¿Quién duda que fumar mata, o que la tele seca el cerebro?. La cuestión radica en que estas relaciones hay que intentar cuantificarlas de una forma objetiva ya que, en caso contrario, siempre habrá alguien que pueda ponerlas en duda. Para ello, habrá que utilizar algún parámetro que estudie si nuestras dos variables varían de forma relacionada.
Cuando las dos variables son dicotómicas la solución es sencilla: podemos usar la odds ratio. En el caso de la tele y el daño cerebral podríamos utilizarla para calcular si realmente es más probable que tengan los sesos secos los que ven la tele que los que no (aunque yo no perdería el tiempo). Pero, ¿qué ocurre si las dos variables son continuas?. Aquí no nos vale la odds ratio, sino que hay que emplear otras herramientas. Veámoslo con un ejemplo.
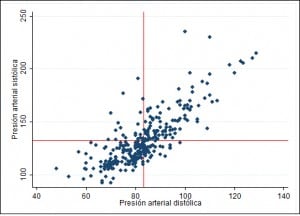
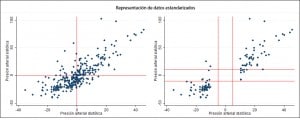
En el primero se muestran los valores de presión estandarizados (cada valor menos la media). Ya vemos que la mayor parte de los puntos están en los cuadrantes inferior izquierdo y superior derecho. Estos todavía se ve mejor en el segundo gráfico, en el que me he comido los valores de sistólica entre ±10 mmHg y de diastólica entre ±5 mmHg alrededor del cero, que serían las medias estandarizadas. Vamos a ver si podemos cuantificar esto de alguna manera.
Recordáis que la varianza medía cuánto variaban los valores de una distribución respecto de la media. A cada valor se le restaba la media, se elevaba al cuadrado para que fuese siempre positivo (y no se anulasen las diferencias positivas con las negativas), se sumaban todas estas diferencias y se dividía por el tamaño de la muestra (en realidad, por el tamaño de la muestra menos uno, y no preguntéis porqué, solo los matemáticos lo saben). Ya sabéis que la raíz cuadrada de la varianza es la desviación típica o desviación estándar, la reina de las medidas de dispersión.
Covarianza
Pues bien, con una pareja de variables podemos hacer una cosa similar. Calculamos, para cada pareja, las diferencias con sus medias y multiplicamos estas diferencias (es el equivalente a la elevación al cuadrado de la diferencia que hacíamos con la varianza). Por último, sumamos todos estos productos y los dividimos entre el tamaño de la muestra menos uno, obteniendo así está versión de la varianza de las parejas que se llama, como no podía ser de otra forma, covarianza.
¿Y qué nos dice el valor de la covarianza?. Pues, poca cosa, ya que dependerá de las magnitudes de las variables, que pueden ser diferentes según de qué estemos hablando. Para esquivar este problemilla recurrimos a una solución muy socorrida en este tipo de situaciones: estandarizar.
Coeficiente de correlación lineal de Pearson
De esta forma, dividimos las diferencias respecto a la media por sus desviaciones estándar, obteniendo así el mundialmente famoso coeficiente de correlación lineal de Pearson.
Bueno es que sepáis que, en realidad, Pearson solo hizo el desarrollo inicial y que el verdadero padre del coeficiente de marras fue Francis Galton. El pobre estuvo toda su vida intentando hacer algo importante porque tenía celos de su primo, mucho más famoso, un tal Charles Darwin, que me parece que escribió algo sobre unas especies que se comen unas a otras y que decía que el secreto está en procrear lo más posible para sobrevivir.
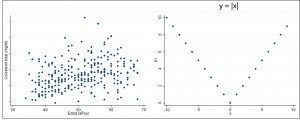
Si r es mayor que cero quiere decir que la correlación es positiva, de forma que las dos variables varían en el mismo sentido: cuando una aumenta, también lo hace la otra y, al revés, cuando una disminuye también disminuye la segunda. Se dice que esta correlación positiva es perfecta cuando r vale 1. Por otra parte, cuando r es negativo quiere decir que las variables varían en sentido opuesto: cuando una aumenta la otra disminuye, y viceversa. Una vez más, la correlación es perfecta cuando r vale -1.
Correlación lineal no implica causalidad
Es fundamental entender que correlación tampoco implica obligatoriamente causalidad. Ya dijo Stephen J. Gould, en su libro «La falsa medida del hombre», que asumir este hecho es uno de los dos o tres errores más graves y frecuentes del razonamiento humano. Y debe ser verdad porque, por más que he buscado, no he encontrado ningún primo suyo que le hiciese sombra, lo que me induce a pensar que lo dijo porque estaba convencido de ello. Así que ya lo sabéis, aunque cuando hay causalidad suele haber correlación, al revés no siempre ocurre lo mismo.
Condiciones necesarias para la correlación lineal
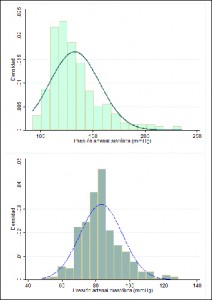
Para esto podemos utilizar pruebas estadísticas como la de Kolmogorov-Smirnov o de Shapiro-Wilks, pero muchas veces basta con representar los histogramas con las curvas de frecuencias y ver si se ajustan. En nuestro caso, la diastólica puede que se ajuste a una normal, pero por la sistólica no pondría la mano en el fuego. Otra pista nos la da la nube de puntos del gráfico inicial: la forma elíptica o en balón de rugby nos indica que, probablemente, las variables siguen una distribución normal. Por último, la tercera comprobación es asegurar que las muestras son aleatorias. Además, solo podemos usar r dentro del rango de datos obtenidos. Si extrapolamos fuera de este rango podemos cometer errores.
Una última advertencia: no confundáis correlación con regresión. La correlación investiga la fuerza de la relación lineal entre dos variables continuas y no es útil para estimar el valor de una variable basándose en el valor de la otra. Por otra parte, la regresión (lineal, en este caso) investiga la naturaleza de la relación lineal entre dos variables continuas. La regresión sí nos sirve para predecir el valor de una variable (la dependiente) basándonos en la otra (la variable independiente). Esta técnica nos proporciona la ecuación de la recta que mejor se adapta a la nube de puntos, con dos coeficientes que nos indican el punto de corte con el eje de ordenadas y la pendiente de la recta.
Nos vamos…
¿Y qué pasa si las variables no siguen una distribución normal?. Pues que no podemos usar el coeficiente de Pearson. Pero no desesperéis, tenemos el coeficiente de Spearman y toda una batería de pruebas basadas en los rangos de los datos. Pero esa es otra historia…

Me ha gustado mucho tu entrada. Lo has explicado perfecto. Me gustaria dejar dos comentarios. El primero en relacion a el valor de r cercano a 0 no indica exactamente ausecia de relación entre las dos variables sino ausencia de relación lineal. Una relación curvilinea ( o sea en un rango de valores, cuando una variable aumenta la otra disminuye y a partir de un determinado nivel cuando aumenta una aumenta la otra) daria una r de 0.
Por otro lado comentar un uso ndebido de r que se ve con frecuencia. Si yo mido un determinado parametro por dos metodos diferentes ( ej los valores de calprotectina en heces con un test rápido o con un ELISA) que me dan un valor cuantitativo, no puedo evaluar la concordancia de los dos metodos con un coeficiente de correlacion de Pearson sino que tendria que usar una prueba de concirdancia ( p ej : kappa)
Cierto. Puedes leer la entrada titulada «¿Un buen acuerdo?», que va sobre concordancia.