La prueba exacta de Fisher.

Hoy vamos a ver una de las historias, en mi humilde opinión, más bonitas de la historia de la bioestadística. Claro que seguramente haya historias mejores, ya que mi ignorancia histórica en general es más grande que el número de decimales del número pi.
Una historia de té y números
Imaginaos que estamos en la estación de Rothamsted, un centro de investigación agraria situado en Harpenden, en el condado inglés de Hertfordshire. Nos situamos en algún momento del comienzo de la década de los años 20 del siglo pasado.
Tres científicos, muy británicos ellos, se disponen a tomar el té. Son dos hombres y una mujer. Ella es Blanche Muriel Bristol, una experta en algas y hongos. Con ella está William Roach, un bioquímico que, además, está casado con Muriel.
El tercero es un genetista que ha comenzado a trabajar en la estación y que con el tiempo se hará famoso por ser uno de los fundadores de la genética de poblaciones y del neodarwinismo, además de algunas otras cosillas, como el concepto de hipótesis nula y contraste de hipótesis. Sí, amigos, es el gran Ronald Fisher.
Fisher prepara las tazas de té y, galantemente, ofrece la primera a Muriel, que la rechaza. Mira Ronald, le dice, a mi me gusta el té con leche, pero solo si se echa la leche en la taza antes que el té. Si se hace al revés, le da un sabor que no me gusta nada.
Fisher piensa que Muriel le está tomando el pelo, así que insiste, pero ella sigue en sus trece. Creo que entonces Fisher debió cambiar de idea y pensar que, en realidad, Muriel era un poco tonta, pero el marido salió al rescate de su mujer. William propone preparar 8 tazas de té y, al azar, poner la leche antes en 4 tazas y después en las restantes.
Para sorpresa de Fisher, Muriel adivina el orden en que había sido servida la leche de las ocho tazas, aunque no le dejan probar más de dos tazas a la vez. ¿Suerte o un paladar privilegiado?
Este, que fue uno de los primeros experimentos aleatorizados de la historia, si no el primero, dejó a Fisher muy pensativo. Así que desarrolló un método matemático para conocer la probabilidad de que Muriel hubiese acertado por pura casualidad. Y este método es el objeto de nuestra entrada de hoy: la prueba exacta de Fisher.
Aclaremos antes unos conceptos
Antes de entrar de lleno en la prueba exacta de Fisher, vamos a aclarar una serie de conceptos para entender bien lo que vamos a hacer.
Cuando queremos hacer un contraste de hipótesis entre dos variables cualitativas (en este caso, para comprobar su independencia) podremos emplear varias pruebas que comparen sus frecuencias o sus proporciones.
Si los datos son independientes, podemos optar por una prueba aproximada, como la de la ji-cuadrado, o por una prueba exacta, como la de Fisher. Si los datos son apareados, podremos hacer una prueba de McNemar (para tablas de contingencia 2×2) o utilizar el método de la Q de Cochran (para tablas 2xk).
Y hemos hablado de pruebas exactas y aproximadas. ¿Qué significa esto?
Las pruebas aproximadas calculan un estadístico con una distribución de probabilidad conocida para, según este valor, conocer la probabilidad de que dicho estadístico adquiera valores iguales o más extremos que el observado. Es una aproximación que se hace en el límite cuando el tamaño muestral tiende a infinito.
Por su parte, las pruebas exactas calculan la probabilidad de obtener los resultados observados de forma directa. Esto se hace generando todos los posibles escenarios que van en la misma dirección de la hipótesis observada y calculando la proporción en los que se cumple la condición que estemos estudiando.
¿Qué es mejor, una prueba aproximada o una exacta?
Pues la gente que sabe de estas cosas no termina de ponerse de acuerdo.
Los métodos aproximados son más sencillos desde el punto de vista de cálculo, pero con la potencia computacional de los ordenadores actuales, no parece ser una razón para elegirlos. Por otra parte, los exactos son más precisos cuando el tamaño de la muestra es más pequeño o cuando alguna de las categorías tiene un número bajo de observaciones.
Pero si el número de observaciones es muy alto, el resultado es similar utilizando un método exacto o uno aproximado.
Como regla de andar por casa, se recomienda utilizar una prueba exacta cuando el número de observaciones es menor de 1000 o cuando haya algún grupo con un número de eventos esperados menor de 5. De todas formas, si tienes un ordenador, no entiendo porque hay que liarse tanto: utiliza uno exacto.
Todo esto no quiere decir que no podamos utilizar una prueba aproximada si la muestra es pequeña, pero tendremos que aplicar una corrección de continuidad, tal como vimos en una entrada anterior.
La prueba exacta de Fisher
La prueba exacta de Fisher es el método exacto utilizado cuando se quiere estudiar si existe asociación entre dos variables cualitativas, es decir, si las proporciones de una variable son diferentes en función del valor de la otra variable.
En principio, parece que Fisher lo diseñó con la idea de comparar dos variables cualitativas dicotómicas. Dicho de forma más sencilla, para utilizarlo con tablas 2×2.
Sin embargo, también hay extensiones del método para realizarlo con tablas mayores. Muchos programas estadísticos son capaces de hacerlo, aunque, lógicamente, exprimen más el funcionamiento del ordenador. También podéis encontrar calculadoras disponibles en Internet.
La prueba de Fisher parte de la hipótesis nula de que las dos variables son independientes, esto es, los valores de una no dependen de los valores de la otra.
La única condición necesaria es que las observaciones de la muestra sean independientes entre sí. Esto se cumplirá si el muestreo es aleatorio, si el tamaño muestral es inferior al 10% del tamaño de la población y si cada observación contribuye únicamente a uno de los niveles de la variable cualitativa.
Además, las frecuencias marginales de las filas y las columnas de las tablas de contingencia de los diferentes escenarios posibles deben permanecer fijas. No os preocupéis por esto, se entenderá mejor cuando veamos un ejemplo. Si esto no se cumple, podemos seguir usando la prueba, pero dejará de ser exacta y se volverá más conservadora.
Cálculo del valor de p
Tras mucho pensar en el problema del té y las habilidades de Muriel Bristol, el genial Fisher demostró que podía calcular la probabilidad de cualquiera de las tablas de contingencia utilizando para ello la distribución de probabilidad hipergeométrica, según la fórmula de la figura.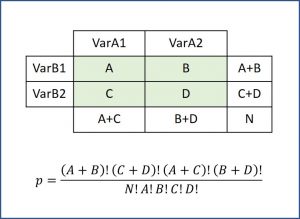
Así, la prueba de Fisher calcula las probabilidades de todas las posibles tablas y suma las de aquellas que tengan valores de p menores o iguales que la tabla observada. Esta suma, multiplicada por dos, nos proporciona el valor de p para un contraste de hipótesis bilateral, o de dos colas.
Ya solo nos quedará, según el valor de p, resolver nuestro contraste de hipótesis de forma similar a como lo hacemos con cualquier otra prueba de contraste.
Veamos un ejemplo
Para acabar de entender todo lo que hemos dicho, vamos a repetir el experimento del té pero yo, en lugar de a Muriel, le voy a pedir a mi primo que nos eche una mano, que hace mucho tiempo que no le damos la murga con nuestras cosas.
Claro, a mi primo no puedo hacerle beber té, así que vamos a ver si sabe diferenciar si lo que está bebiendo es whisky escocés o irlandés. Él afirma que es capaz de distinguir un whisky escocés de cualquier otra cosa.
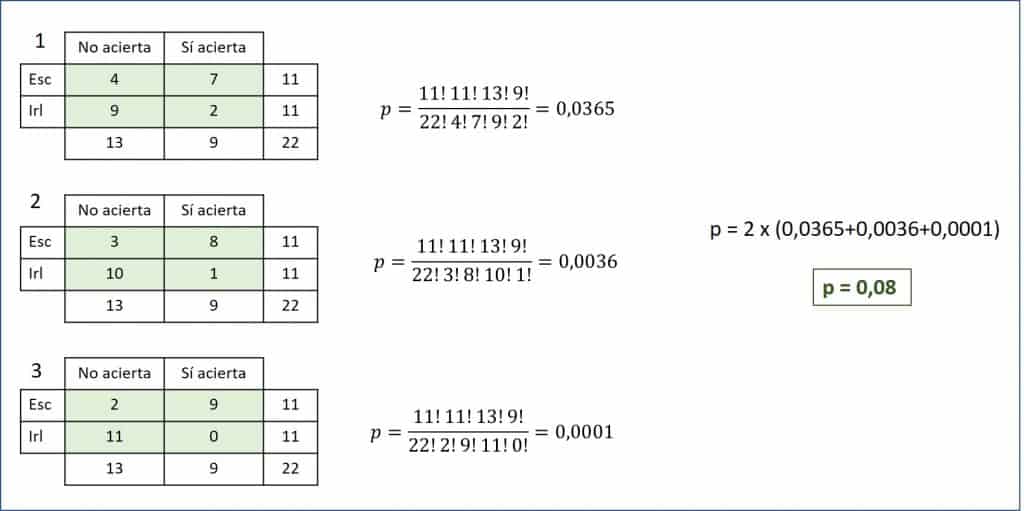
Así, para probar su resistencia al alcohol, además de las habilidades de su paladar, le ofrezco al azar 11 chupitos de whisky escocés y otros 11 de irlandés.
Los resultados podéis verlos en la primera tabla de la figura adjunta.
Como veis, acierta en 7 de los 11 escoceses y solo en 2 de los 11 irlandeses. Parece que tiene razón en su afirmación y que tiene un paladar refinado. Pero nosotros, al igual que hizo Fisher con Muriel, vamos a ver si solo ha tenido suerte.
Como hemos dicho más arriba, hay que calcular las posibles tablas que tengan una probabilidad menor que la observada y dentro del sentido de nuestra hipótesis. Esto lo haremos reduciendo la frecuencia mínima de cada una de las columnas hasta que alguna llegue a cero.
Además, ajustaremos las otras casillas para que los marginales se mantengan constantes. En caso contrario, ya sabemos que la prueba dejaría de ser exacta. Podéis ver las dos tablas posibles hasta que los aciertos con whisky irlandés llegan a cero.
Ya solo nos queda calcular la probabilidad de cada tabla, sumarlas todas y multiplicar por dos. Obtenemos un valor de p = 0,08 para un contraste bilateral. Como la hipótesis nula dice que la capacidad de acertar no se influye por el tipo de whisky, no podemos rechazar que el alarde de mi primo solo haya sido una cuestión de suerte.
Haz el cálculo de forma automática
Ya llegando al final de esta entrada, advertir que a nadie se le ocurra hacer una prueba exacta de Fisher de forma manual. Este ejemplo tan absurdo es sumamente simple, pero seguro que nuestros experimentos son un poco más complejos. Utiliza una aplicación informática o una calculadora de Internet.
Vamos a resolver el ejemplo utilizando el programa R.
En primer lugar, introducimos los datos para construir la tabla de contingencia con estos dos comandos consecutivos:
datos <- data.frame(tipow = c(rep(«irl»,11), rep(«esc»,11)), acierto = c(rep(TRUE,2), rep(FALSE,9), rep(TRUE,7), rep(FALSE,4)))
tabla <- table(datos$tipow, datos$acierto, dnn = c(«Tipo whisky», «Acierta»))
Finalmente, realizamos la prueba de Fisher:
fisher.test(x = tabla, alternative = «two.sided»)
En la pantalla de salida, el programa nos proporciona el valor de p (p=0,08), su intervalo de confianza y la odds ratio entre las dos variables. Recordad que la prueba de Fisher solo nos dice si hay diferencia estadísticamente significativa, pero si queremos medir la fuerza de la asociación entre las dos variables tenemos que recurrir a otro tipo de medidas.
Y al que esté buscando el valor del estadístico de Fisher entre los datos de salida del programa, siento decirle que tiene que volver a leerse la entrada desde el principio.
Ya lo hemos dicho, las pruebas exactas calculan la probabilidad directa sin necesidad del cálculo previo de un estadístico que siga una distribución de probabilidad conocida. El estadístico de Fisher no existe.
Nos vamos…
Y aquí lo vamos a dejar por hoy. Hemos visto cómo la prueba exacta de Fisher nos permite estudiar la independencia de dos variables cualitativas pero que nos exige una condición: que las frecuencias marginales de filas y columnas permanezcan constantes.
Y esto puede ser un problema, porque en muchos experimentos biológicos no podremos o no estaremos seguros de cumplir este requisito. ¿Qué pasa entones? Como siempre, hay varias alternativas.
La primera, seguir utilizando la prueba. El inconveniente es que deja de ser una prueba exacta y pierde sus ventajas respecto a las pruebas aproximadas. Pero podríamos usarla.
La segunda, utilizar otra prueba de contraste que no pierda potencia cuando los marginales de la tabla no sean fijos como, por ejemplo, la prueba de Barnard. Pero esa es otra historia…