Teorema del límite central.

Si uno hace caso de las películas, tenemos más maneras de extinguirnos que de preparar una tortilla: meteoritos, zombis, pandemias, robots asesinos, alienígenas poco dialogantes, inteligencia artificial con complejo de dios, y, por supuesto, nuestra favorita: nosotros mismos, arruinándolo todo a fuego lento.

Dicen que el ser humano es la especie más inteligente del planeta. También dicen que los cuervos pueden recordar caras humanas y resolver acertijos más rápido que muchos estudiantes con resaca. ¿A quién creemos más? Porque viendo cómo vamos, da la impresión de que la inteligencia humana está en oferta: se gasta rápido, se repite mucho y rara vez viene con instrucciones. Si nos extinguimos, no será por un meteorito o por un virus letal… será porque hicimos un TikTok bebiendo lejía, mientras discutíamos en X si la Tierra es plana.

Pero aquí viene lo gracioso: a pesar del caos, del ruido, de las redes, de las fake news y de los discursos que suenan a PowerPoint hecho a última hora por alguien que no ha dormido… todo sigue una lógica. Una lógica numérica, oculta, pero obstinada. Porque por más que nos creamos únicos o visionarios, al final nos comportamos como datos. Miles de millones de puntos de datos, con sus medias, sus varianzas… y, sobre todo, con su error estándar. Ese pequeño margen que nos recuerda que una sola observación no basta para entender el conjunto.

En esta entrada vamos a hablar del teorema del límite central, esa gema estadística que explica cómo, en medio del caos, surge el orden. Aunque cada individuo sea un disparate andante, cuando los miramos en grupo, empiezan a parecerse a algo… incluso a una campana de Gauss. Y ahí está la ironía: tal vez nos salvemos no por ser listos, sino porque los errores se cancelen entre sí. Eso, o nos extinguirá el algoritmo.

Un mundo lleno de ruido

En lo individual, los llamados seres humanos somos difíciles de entender. Hacemos cosas extrañas, tomamos decisiones discutibles y, a veces, damos respuestas tan aleatorias como un dado mal tirado. No es de extrañar pues que, en nuestra práctica clínica, nos encontremos con ese mismo caos: un paciente con fiebre responde al paracetamol en diez minutos, a otro no le baja la temperatura ni con hielo, y un tercero jura que lo curó la sopa de su abuela.

Pero cuando agrupamos suficientes casos, ocurre algo curioso. Lo que parecía ruido empieza a mostrar patrones, como si la locura individual se amortiguara en el conjunto. Es aquí donde entra en juego el teorema del límite central, ese principio que, aunque suena a nombre de película de ciencia ficción, en realidad es una de las bases más sólidas para poder confiar en los datos, tomar decisiones con respaldo numérico y sustentar muchos de los procedimientos estadísticos que usamos en investigación clínica.

El teorema del límite central

Como ya hemos dicho, el teorema del límite central es una de las herramientas más poderosas y útiles de toda la estadística. De forma resumida, afirma que, si tomamos un número suficientemente grande de muestras aleatorias de una misma población y calculamos la media de cada muestra, la distribución de esas medias tenderá a seguir una distribución normal, con independencia de cómo sea la distribución original de los datos.

En otras palabras, aunque los datos individuales sean caóticos, sesgados o extremos, las medias de muchas muestras se ordenan espontáneamente en una flamante curva de Gauss, simétrica y predecible. Si me permitís la licencia poética, podría decirse que la normalidad surge del caos.

Además de su inherente belleza, esto tiene implicaciones prácticas enormes. Nos permite trabajar con datos clínicos reales, que rara vez siguen una distribución ideal, y aplicar herramientas estadísticas que sí asumen normalidad, las llamadas técnicas paramétricas, que son más precisas y potentes que las no paramétricas, que no necesitan asumir ninguna distribución de los datos en la población.

Pero no os confundáis, no es que los datos se vuelvan normales mágicamente; lo que se normaliza es la distribución de las medias de las muestras repetidas que extraemos de la población, y eso basta para aplicar pruebas paramétricas, calcular intervalos de confianza o hacer inferencias.

La estadística nos muestra que, aunque los casos individuales puedan parecer caóticos o impredecibles, al analizarlos en conjunto emerge una estructura, una lógica subyacente que permite comprender el comportamiento del grupo como un todo.

Una metamorfosis matemática

El teorema del límite central tiene una demostración matemática sublime, pero al alcance de unos pocos afortunados, entre los cuales no me encuentro, así que vamos a ver un ejemplo práctico para que creáis lo que os he contado. Vamos a ver como una distribución discreta y sesgada, como la binomial, se transforma mágicamente en una majestuosa campana.

Para ello, imaginemos un escenario clínico muy simple: se acaba de desarrollar un nuevo tratamiento para esa temible enfermedad que es la fildulastrosis, que ha mostrado un 20 % de probabilidades de éxito. Es decir, de cada 10 pacientes tratados, en promedio, dos responden favorablemente. Estamos ante una variable binomial: cada paciente tiene una probabilidad fija de éxito (p = 0,2) y solo dos posibles resultados (éxito o fracaso).

Supongamos que aplicamos el tratamiento a 1000 muestras independientes de 10 pacientes cada una y registramos cuántos pacientes responden al tratamiento en cada grupo. La media esperada es de 2 éxitos por grupo, pero los valores oscilan entre 0 y 10. La distribución resultante es claramente irregular: discreta, con picos visibles, y asimétrica hacia la derecha, tal como veis en la figura adjunta. La variabilidad es elevada y la distribución está lejos de parecerse a una normal.

Ahora imaginad que repetimos el experimento con 1000 muestras de 30 pacientes. La media esperada es de 6 éxitos por grupo. En este caso, la distribución empieza a suavizarse: los valores más frecuentes se sitúan entre 4 y 8 éxitos, los extremos son menos comunes, y la forma general empieza a parecer simétrica. Aunque seguimos en el terreno de variables discretas, la distribución se aproxima a una forma de campana.

Por último, hacemos la prueba con 1000 muestras de 100 pacientes. La media esperada ahora es de 20 éxitos. La distribución resultante es casi indistinguible de una normal: simétrica, continua en apariencia, y con la mayoría de los valores entre 17 y 23. Aunque seguimos contando éxitos (una variable binomial), la forma se ha transformado en una curva suavizada, perfectamente aproximable con una distribución normal.

Vemos, pues, que, al aumentar el tamaño de las muestras, incluso variables binarias se comportan como si fueran normales. Este comportamiento es lo que permite que gran parte de los análisis estadísticos, como la estimación de intervalos de confianza y las pruebas de contraste de hipótesis, se puedan aplicar con seguridad, incluso cuando los datos originales no siguen una distribución normal.

No te fíes solo de la media

Si pensamos en el ejemplo anterior, repitiendo muchas veces el experimento llegamos a tener una idea aproximada del valor del parámetro en la población, ya que no podemos medirlo de manera directa. Así, la media de los resultados se corresponde con una estimación puntual de ese valor inabarcable.

Pero el teorema del límite central va más allá, ya que, como nuestras muestras tienden a una distribución normal, podemos también cuantificar cuánto varían esas medias, lo que nos dará una idea de la fiabilidad de nuestra estimación.

Esa medida de variabilidad de las medias no es otra que la desviación estándar de las medias de la distribución, la medida de dispersión más conocida. Sin embargo, en este caso particular le damos un nombre diferente: error estándar de la media.

Pero lo más curioso es que, para calcular el error estándar de la media, no es necesario recoger un montón de muestras, calcular las medias de cada una y juntarlas para calcular su desviación estándar. Podemos hacerlo a partir de nuestra muestra, solo necesitamos dividir nuestra media muestral entre la raíz cuadrada del tamaño de nuestra muestra:

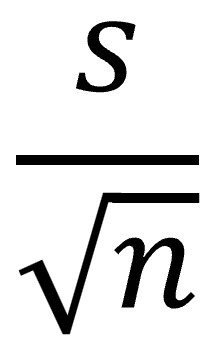
Si nos fijamos un poco en la fórmula, entenderemos que, cuanto más grande sea la muestra, menor será el error estándar y, por tanto, nuestra estimación de la media será más precisa.

Esto tiene sentido si lo pensamos un poco y nos fijamos en el ejemplo que vimos más arriba: una media calculada con 10 pacientes puede variar mucho de una muestra a otra, pero una media calculada con 500 pacientes es más estable, menos sensible a los valores extremos o al azar. Por ello, el error estándar es, en esencia, una forma de medir cuánta incertidumbre hay en el promedio que estamos usando como estimador.

El error estándar es importante porque permite construir intervalos de confianza, calcular pruebas de significación, o incluso evaluar si una diferencia entre grupos podría deberse al azar. Y, aunque a veces se confunde con la desviación estándar (que mide la variabilidad de los datos individuales), el error estándar no habla de los individuos de la muestra, sino de la confianza en el valor promedio que obtenemos de esa muestra al calcular una estimación por intervalo, con el nivel de confianza que establezcamos.

Nos vamos…

Y ya solo nos queda despedirnos, así que voy a intentar dar una nota un poco más optimista que la del comienzo de esta entrada.

Hemos visto que el teorema del límite central nos enseña que, en medio del ruido y el caos de los datos individuales, siempre existe la posibilidad de encontrar un orden. Que nuestras estimaciones, por más incertidumbre que traigan de la mano, pueden apoyarse en principios sólidos que nos permiten entender no solo sus valores, sino también cuánta confianza podemos depositar en ellas.

Es evidente que cuantificar la incertidumbre de una estimación no es un lujo estadístico, sino una necesidad para no caer en interpretaciones erróneas, que pueden llevarnos a conclusiones precipitadas o, directamente, a malas decisiones. Y la brújula que nos permite orientarnos en este camino no es otra que el error estándar de la media, con el que construiremos nuestros apreciados intervalos de confianza. Pero esa es otra historia…