Prueba de los signos.

La prueba de los signos compara dos medianas utilizando para ello el sentido de los valores respecto a la media y la probabilidad binomial.
En el mundo de la ciencia en general, y de la medicina en particular, estamos habituados a hacer todo de forma muy precisa y detallada. ¿Quién no ha pautado alguna vez 123,5 mg de amoxicilina cada ocho horas?. Sin embargo, las cosas pueden hacerse también a bulto y sin hacer ninguna chapuza. Claro que el bulto tiene que seguir unas reglas determinadas. Veamos un ejemplo.
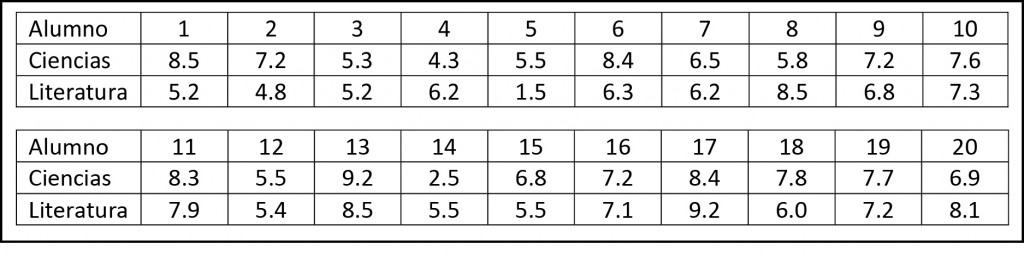
Supongamos que queremos saber si nuestro sistema educativo es tan bueno como debería. Tomamos una clase de veinte alumnos de primer año de secundaria y les pasamos dos exámenes facilitos, uno sobre ciencias naturales y otro sobre literatura. Las notas podéis verlas en la tabla adjunta.
Si os molestáis en calcularlo, los alumnos sacan en ciencias una media de 6,8 puntos con una desviación estándar (DS) de 1,6. Por su parte, en literatura sacan una media de 6,4 con una DS de 1,7. Parece, pues, que nuestros alumnos están mejor preparados en ciencias naturales que en sociales. La pregunta es inmediata: ¿esto puede extrapolarse a todos los alumnos de nuestro sistema educativo?.
Hagamos el cálculo
Para saberlo solo tenemos que hacer una prueba de la t de Student, suponiendo que la distribución de las notas se ajuste a una normal, lo cual parece razonable. Podríamos pedírselo a un programa de estadística o hacerlo nosotros calculando la diferencia de medias y el error estándar de la diferencia para obtener la t y ver su probabilidad, para así saber si podemos aceptar o rechazar nuestra hipótesis nula, que en este caso es que la diferencia observada se debe al azar y los conocimientos de nuestros chicos son similares en ambas asignaturas.
Pero hemos dicho que lo íbamos a hacer a bulto, de forma mucho más simple. Si os fijáis, la mayor parte de los alumnos (quince) tienen mejor nota en ciencias, mientras que solo cinco (los números 4, 8, 14, 17 y 20) tienen mejor nota en literatura. Pensemos ahora un poco.
Si la hipótesis nula de que los conocimientos de las dos asignaturas son similares fuese cierta, la probabilidad de tener mayor nota en cualquiera de las dos sería del 50% (0,5). Quiere decir que diez alumnos tendrían mejor nota en ciencias y diez en literatura. Así que nos preguntamos: ¿cuál es la probabilidad de que la diferencia observada (quince en lugar de diez) se deba al azar?.
Y esto, señoras y señores, es un típico caso de probabilidad binominal, donde n=20, p=0,5 y k>14 (siendo n el total de alumnos, p la probabilidad de tener más nota en ciencias y k el número de alumnos con más nota en ciencias). Podemos resolver la ecuación según la fórmula de la probabilidad binomial o utilizar una de las calculadoras disponibles en Internet para llegar a la conclusión de que la probabilidad de que quince saquen más nota en ciencias por azar es del 2,07%. Por tanto, al ser menor del 5%, rechazamos nuestra hipótesis nula y concluimos que a nuestros alumnos se les dan mejor las ciencias, siempre, claro está, con una probabilidad de error de tipo 1 del 5%.
Prueba de los signos
Esta prueba que acabamos de ver tiene el bonito nombre de prueba de los signos, y es una de las muchas pruebas no paramétricas que pueden utilizarse para realizar inferencia estadística. Como habéis visto, no tiene en cuenta ni el valor de los parámetros (por algo se llama no paramétrica) ni la magnitud de las diferencias, pero tampoco necesita que los datos sigan una distribución normal ni que la muestra sea muy grande.
Por eso suelen utilizarse las pruebas no paramétricas cuando no puede asumirse normalidad o cuando la muestra es pequeña, pero podríamos usarlas en cualquier situación. ¿Y por qué no se usan siempre?. Pues fundamentalmente porque son más exigentes que las pruebas paramétricas y precisan que la magnitud del efecto sea mayor para poder rechazar la hipótesis nula.
Nos vamos…
Y con esto terminamos esta entrada. No penséis que todas las pruebas no paramétricas son igual de sencillas. Aquí hemos hablado de una forma sencilla de comparar dos medias (en realidad, dos medianas), pero también las hay para comparar más de dos, como la prueba de Kruskal-Wallis. Pero esa es otra historia…