Análisis de normalidad.

Para comprobar la normalidad de una variable disponemos de tres estrategias posibles: los métodos basados en contrastes de hipótesis, los basados en representaciones gráficas y los llamados métodos analíticos.
Cuando pensamos en matemáticas, en general, y en estadística, en particular, tenemos tendencia a imaginar un mar de números y fórmulas complicadísimas.
Cuando tratamos de describir la relación entre dos variables, podemos emplear cientos de palabras para transmitir un concepto. Pero muchas de estas veces, podemos ahorrar tiempo y tinta y recurrir a la representación de una sola fórmula.
Las fórmulas estadísticas tienen su belleza, no se puede negar. Todo lleno de letras griegas mayúsculas y minúsculas, letras con barra o con sombrero, subíndices y superíndices para repartir, etc. En muchas ocasiones, un vistazo a la fórmula será suficiente para explicar un concepto que requeriría varías líneas de texto en lenguaje corriente.
Sin embargo, hay veces que la información puede ser tan compleja que no nos ayude disponer solo de la fórmula que describa la situación. En estas ocasiones se aplica ese adagio popular que afirma que una imagen vale más que mil palabras. Estamos hablando de la representación gráfica de los datos.
Al representar los datos de forma gráfica podemos comprender de forma más rápida, sencilla e intuitiva cómo evolucionan y se relacionan las distintas variables. Los vemos a diario en los medios de comunicación para representar la evolución de los precios, del desempleo, de los contagios de una enfermedad, etc.
Y precisamente de eso, entre otras cosas, vamos a hablar en la entrada de hoy, de cómo utilizar métodos gráficos para ayudarnos a determinar si nuestros datos siguen una distribución normal ya que, como veremos, los métodos numéricos pueden ser poco confiables.
Planteamiento del problema
Ya conocemos la distribución normal y su papel central para poder utilizar las pruebas paramétricas en nuestros contrastes de hipótesis. Para la mayor parte de contrastes es obligado comprobar que nuestros datos siguen una distribución normal antes de elegir la técnica a utilizar.
Los contrastes o análisis de normalidad tratan de analizar cuánto difiere la distribución de nuestros datos (los observados en nuestra muestra) respecto a lo que deberíamos esperar si los datos procediesen de una población en la que la variable siguiese una distribución normal con la misma media y desviación estándar que la observada en los datos de la muestra.
Para esta comprobación disponemos de tres estrategias posibles: los métodos basados en contrastes de hipótesis, los basados en representaciones gráficas y los llamados métodos analíticos.
Análisis de normalidad mediante contrastes de hipótesis
Existen diversas pruebas de contraste de hipótesis para comprobar si los valores de una variable siguen o no una distribución normal.
Al tratarse de contrastes de hipótesis, todos ellos proporcionan un valor de p que representa la probabilidad de encontrar una distribución de los datos como la nuestra, o todavía más alejada de la normalidad, bajo el supuesto de la hipótesis nula de que, en la población, la variable sigue una distribución normal perfecta.
O sea, que para estas pruebas la hipótesis nula es de normalidad. Por lo tanto, si p>0,05, no tendremos motivos para descartar la hipótesis nula y asumiremos que nuestra variable sigue una distribución normal. Si, por el contrario, p<0,05, rechazaremos la hipótesis nula y asumiremos que nuestra variable no sigue una distribución normal en la población.
Pruebas de contraste para el análisis de normalidad
Existen, como ya hemos dicho, diversas pruebas para realizar el análisis de normalidad. Veamos tres de las más utilizadas.
Cuando el tamaño muestral no es muy grande (en general, n<50) la más utilizada es la prueba de Shapiro-Wilk. Es bastante sencilla de realizar con cualquier programa de estadística. Si empleamos R, el comando es shapiro.test(x), donde x es el vector con los datos de la variable en estudio.
Otra prueba de análisis de normalidad muy utilizada es la prueba de Kolmogorov-Smirnov. Esta prueba tiene la ventaja de que permite estudiar si una muestra procede de una población con una distribución de probabilidad con media y desviación estándar determinada, pero que no tiene por qué ser obligadamente una distribución normal.
El comando en R para realizar esta prueba es ks(x, “pnorm”, media(x), desviación estándar(x)).
El inconveniente de la prueba de Kolmogorov-Smirnov es que precisa conocer la media y la varianza poblacional, valores desconocidos en la mayor parte de las situaciones.
Para obviar este inconveniente, se desarrolló una modificación de la prueba, conocida como prueba de Lilliefors, cuyo comando en R es lillie.test(x).
La prueba de Lilliefors, que está totalmente diseñada para el análisis de normalidad, asume que la varianza y la media poblacional son desconocidas, por lo que constituye la alternativa a la prueba de Shapiro-Wilk cuando el tamaño de la muestra es superior a 50.
El problema de las pruebas de contraste
El problema con estas pruebas, de sencilla realización, es que su resultado debe interpretarse siempre con cautela.
Por una parte, son pruebas poco potentes cuando el tamaño de la muestra es pequeño. Al basarse en la hipótesis nula de normalidad, podemos no alcanzar significación estadística por falta de potencia estadística, asumiendo erróneamente que los datos siguen una distribución normal (al no poder rechazar la hipótesis nula).
Por otra parte, cuando la muestra es muy grande, ocurre lo contrario: será suficiente una pequeña desviación de la normalidad para que la prueba nos dé una p significativa y rechacemos la hipótesis nula, cuando la mayor parte de las técnicas paramétricas tolerarían pequeñas desviaciones de la normalidad si la muestra es grande.
Por estos motivos, es aconsejable completar siempre el análisis de normalidad con un método gráfico y no quedarnos solo con el método numérico de contraste de hipótesis.
Análisis de normalidad mediante métodos gráficos
En este caso, una imagen vale más que mil palabras. Observando la representación gráfica de los datos podemos interpretar si su distribución se parece lo bastante a una normal como para asumir que la variable sigue esa distribución en la población o si, por el contrario, se aparta de la distribución normal, digan lo que digan los métodos de contraste.
Los tres gráficos más empleados son el histograma, el gráfico de caja y el gráfico de comparación de cuantiles.
Histograma
Como ya sabemos, el histograma representa la distribución de frecuencias de la variable aleatoria que se estudia.
La forma y distribución de las barras nos ayudarán a interpretar si los valores se distribuyen de forma normal. Para ayudarnos más, suele superponerse la curva de densidad de lo que sería la distribución normal perfecta con una media y desviación estándar igual a la de nuestros datos.
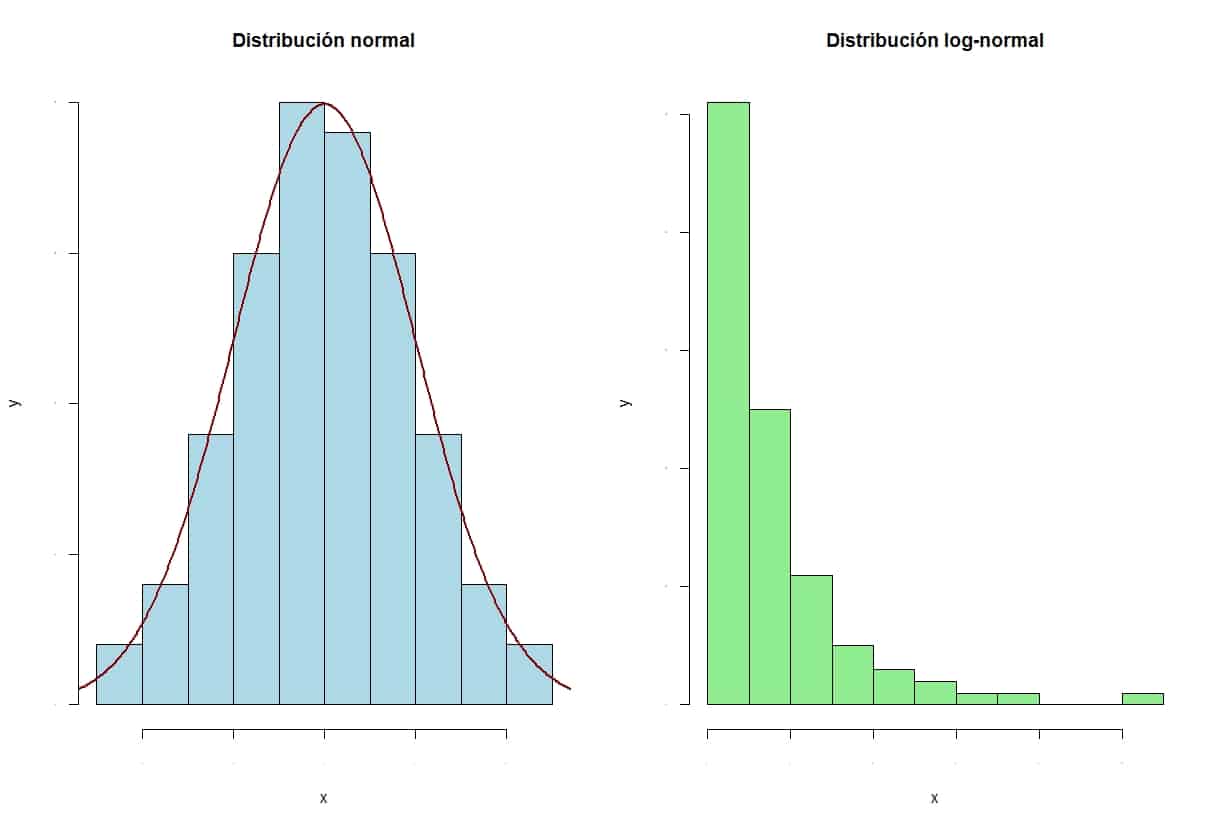
En la figura anterior podéis ver los histogramas de dos distribuciones de valores. La de la izquierda corresponde a una distribución normal. Podéis ver cómo las barras se distribuyen de forma simétrica respecto al valor medio. Además, el perfil de las barras se adapta a la curva normal.
Por otra parte, la de la derecha corresponde a una distribución log-normal. En este caso, vemos como la distribución es claramente asimétrica, con una cola larga hacia la derecha. Viendo este gráfico no dudaríamos: asumiríamos la normalidad de la distribución de la izquierda y la rechazaríamos en el caso de la derecha.
Diagrama de caja
El gráfico de caja, más conocido por su nombre en inglés, boxplot, es utilizado con mucha frecuencia en estadística por sus capacidades descriptivas.
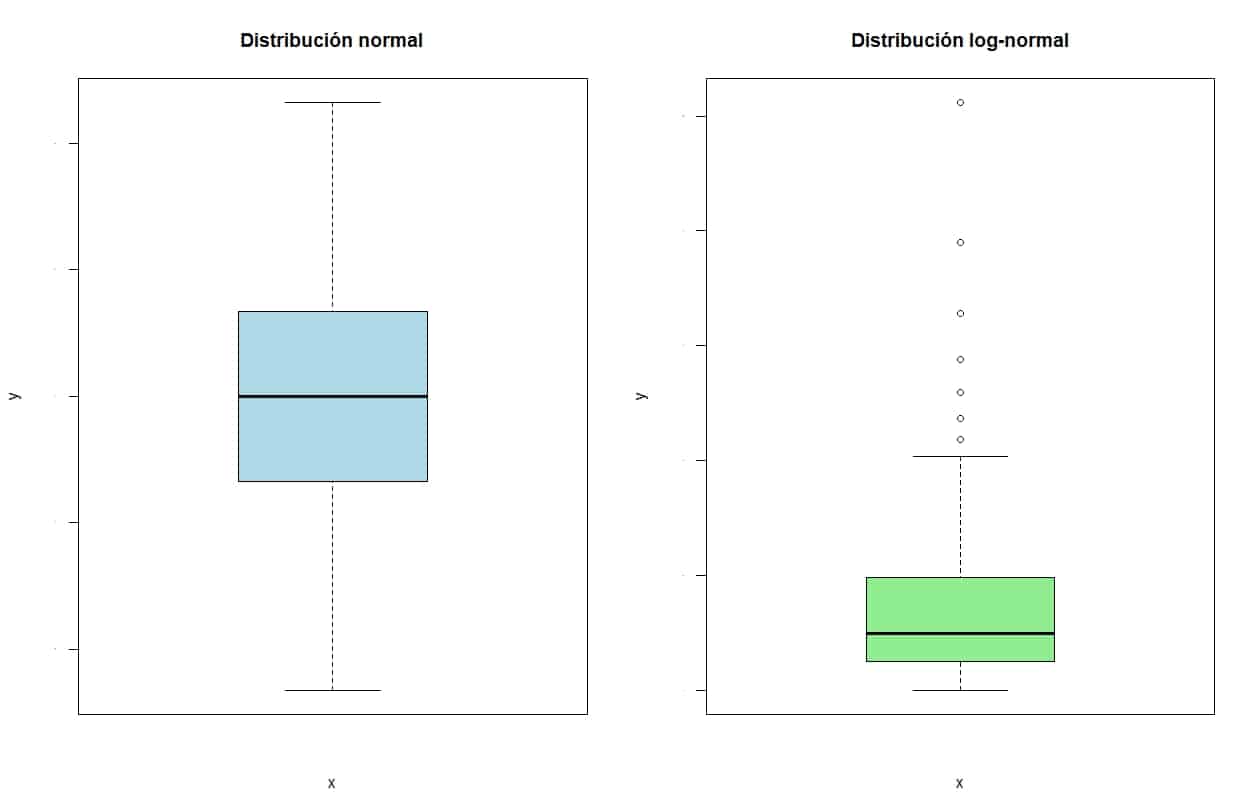
En la figura adjunta podéis ver los diagramas de cajas de las dos distribuciones cuyos histogramas vimos más arriba.
Si observamos cada caja, el borde inferior representa el percentil 25º de la distribución o, lo que es lo mismo, el primer cuartil. Por su parte, el borde superior representa el percentil 75º de la distribución o, lo que es lo mismo, el tercer cuartil.
De esta manera, la amplitud de la caja se corresponde con la distancia entre los percentiles 25º y 75º, que no es otra que el recorrido o rango intercuartílico. Por último, en el interior de la caja hay una línea que representa la mediana (o segundo cuartil) de la distribución.
En cuanto a los “bigotes” de la caja, el superior se extiende hasta el valor máximo de la distribución, pero no puede llegar más allá de 1,5 veces el rango intercuartílico. Si existen valores más extremos, se representan como puntos más allá del extremo del bigote superior.
Y todo esto vale para el bigote inferior, que se extiende hasta el valor mínimo cuando no hay valores extremos o hasta la mediana menos 1,5 veces el rango intercuartílico cuando los haya.
Si os fijáis en el gráfico, la distribución normal tiene una caja simétrica alrededor de la media, con ambos segmentos del recorrido intercuartílico de longitud similar. Por su parte, la log-normal, muestra una clara asimetría, con un segmento superior del recorrido intercuartílico más largo y con varios valores extremos al bigote superior. Es el equivalente a la asimetría con el sesgo hacia la derecha que observábamos en el histograma.
Gráfico de comparación de cuantiles
El gráfico de comparación de cuantiles, también conocido por su apodo en inglés, qqplot, representa los cuantiles de nuestra distribución frente a los cuantiles teóricos que tendría si siguiese una distribución normal con la misma media y distribución estándar que nuestros datos.
Si los datos siguen una distribución normal, se alinearán cerca de la diagonal del gráfico. Cuanto más se alejen, menos probable será que nuestros datos sigan una distribución normal.
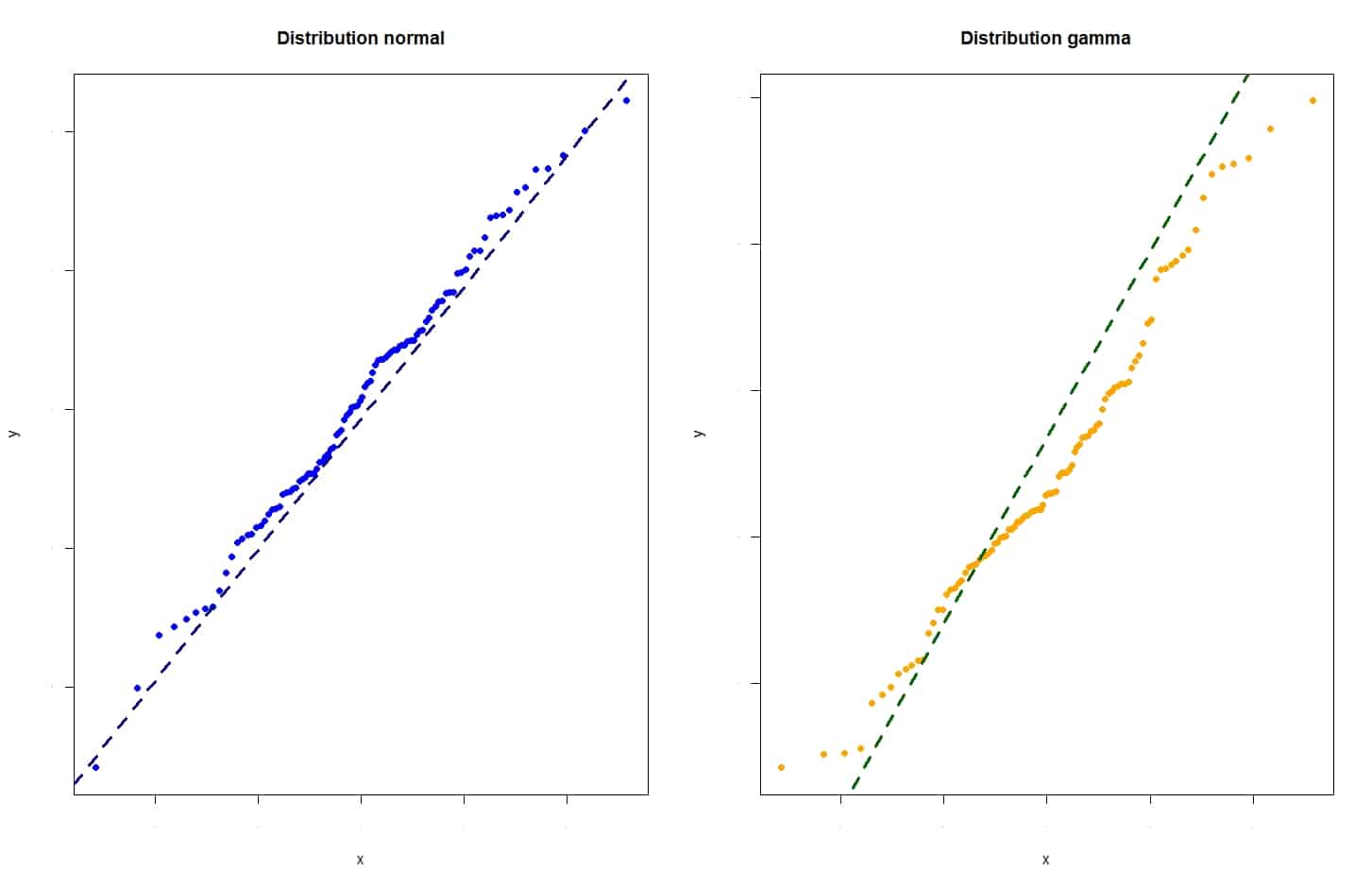
Podéis verlo en la figura que os adjunto, en la que veis el gráfico de cuantiles de una distribución normal y de una distribución gamma.
Podéis comprobar que los puntos se alinean razonablemente de forma rectilínea con la diagonal en el caso de la distribución normal, mientras que los puntos de la gamma forma una línea en forma de S que se aparta de la diagonal.
Nos vamos…
Y con esto lo vamos a ir dejando por hoy.
Hemos visto los principales métodos de contraste de hipótesis para análisis de normalidad y cómo conviene complementarlos siempre con algún método gráfico.
De lo que no hemos hablado nada es de los métodos analíticos. Estos se basan en el análisis de dos de los momentos de la distribución normal, el índice de simetría y el apuntamiento. Pero esa es otra historia…

Pedazo artículo.
Felicidades!
Muchas gracias Xabier. Me alegro mucho de que te haya gustado.