Crossover clinical trial.

Crossover clinical trial allows each patient to receive the study and the control interventions, in a specific order and for a set time.
Mathematicians say that two parallel lines are those which never meet, no matter how far extended. Never? It seems to me that never is too much time. I don’t think anyone has ever extended two parallels long enough to be sure of this statement. Of course, on the other hand, if they end converging it’s that they were not parallels at all, weren’t they?
Those that can converge, and even cross, are the two branches of a parallel trial, resulting in a new design called crossover trial.
Crossover clinical trial
In a classical parallel clinical trial each participant is randomly assigned to one, and only one, of the arms of the trial, to that of the studied 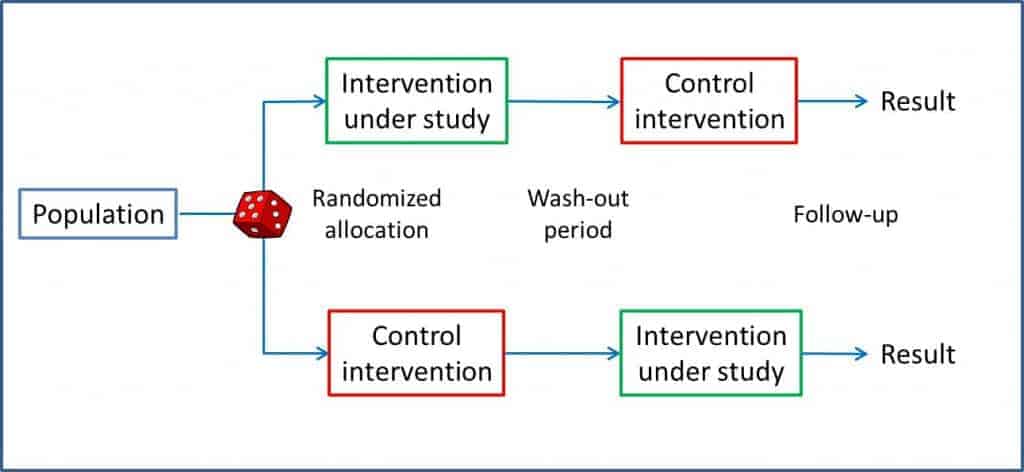
Thus, each subject serves as his own control, experiencing both interventions in a sequence of periods set in a random way and being the two periods separated by a stabilization or washout period. You can see a diagram of this design in the attached figure.
Pros
There are some variations on the theme of crossover trials, depending on the number of participants under the two interventions: all of them (complete trial) or only some of them (incomplete trial). Furthermore, it is possible to extend this type of design and test more than two interventions, leading to different levels of sequence that are named as dual design, Balaam, Latin square, etc., but we’re not going to talk about them in this post.
The main advantage of the crossover studies lies in a feature already discussed: each subject acts as his own control. This may seem unimportant bullshit, but it is not. If you think about it, what we do is to assess the effect of active intervention and control in the same subject, which will get less variability than if we compare the effects on different participants, as is done in the trial in parallel wherein each participant is exposed to only one of the two interventions.
With less variability, the accuracy of the observations is increased, whereby the sample size required to detect a specified difference in treatment effect will decrease. And not a little lower, but the sample required can be reduced significantly compared with what would be needed in the corresponding parallel trial.
This reduction in sample size depends on the correlation between the different outcomes of the study. In the worst case, with zero correlation, the sample is split in half. If the correlation is 0.5, the necessary sample shall be one quarter. But this reduction is increasing as the value of the correlation approaching to one.
As if that were not enough, along with a more accurate estimate, this is less biased, since it assumes a constant response of each subject to the two interventions tested, while testing in parallel trial the measured response is more variable in different subjects.
And cons
But not everything will be advantages for crossover designs. They also raise some drawbacks. The biggest limitation is the pain in the ass that is given to participants with so much intervention and so many periods. And this is important not only for the respect that we should feel for the participants, but it increases the risk of losses during the study. It turns out that crossover studies are more sensitive to losses during follow-up than parallel trials, especially if the number of participants who complete each sequence is different.
Another limitation is that it’s important that subjects are similar at the beginning of each period, so these studies are only useful with chronic diseases in patients with stable symptoms. Nor they serve if the outcome variable produces a permanent effect. Consider the most permanent of all, mortality. If the participant dies in the first period, it will be more than difficult to assess their response in the next period.
In addition, some of its advantages, such as small sample size, becomes in disadvantage at times. This occurs, for example, in Phase III studies in which we want to assess safety, tolerability, efficacy, detection of unpredictable adverse effects, etc. In these cases, the small sample is not only unneeded, but may be inadequate.
Three characteristics of crossover trials
Finally, referring to three weaknesses from the viewpoint of design called residual effect, sequence effect and period effect.
The residual effect occurs in a period when the effect of the intervention of the previous period still persists. Let us think that we have taken a drug and there are still remains in the blood. Obviously this is solved by extending the washout period, but sometimes this is not so easy. Consider an antihypertensive treatment in which the response in the second period is more favorable for the simple fact of being included in the study (placebo effect).
The sequence effect occurs when the order of interventions affect the final result, which we could only properly assess the results of the first intervention.
Finally, it may happen that the patient characteristics change along the study, modifying its response to different interventions. We are facing a period effect.
Crossover clinical trial are, in short, more efficient in terms of sample size that parallel trials, provided that the optimal conditions for their use are met. They are very useful for studies of phase I and phase II in which we want to know the pharmacokinetics and pharmacodynamics, safety, dose titration, etc. In later phases of the development of new drugs they are less useful, especially if, as we have said, we aren’t dealing with a chronic disease with stable symptoms.
We’re leaving…
And here we end with the crossover trials. We have not talked anything about the statistical analysis of the results. In the case of parallel test results of the two branches can be directly compared, but this is not so with crossover trials, in which we must ensure that there has not been a residual, sequence or period effect. But that is another story…
