Vote counting method in reviews.

To get a conclusion on the result of a review, it is not enough with the vote counting method. A weighted measure is nedeed.
No need for anyone to worry. Today we’re not going to talk about politics. Instead, today will talk about something far more interesting. Today we will discuss voting trials in narrative reviews. What am I talking about? Keep reading and you will understand.
Let’s illustrate it with a totally fictitious, besides absurd, example. Suppose we want to know if those who watch more than two hours of TV per day have more risk of suffering acute attacks of dandruff. We go to our favorite database, which can be Tripdatabase or Pubmed and do a search. We get a narrative review with six papers, four of which don’t obtain a higher relative risk of dandruff attacks among couch potatoes and two in which significant differences were found between those who see much or little television.
What do we make of it? Is there a risk in watching too much TV? The first thing that crosses our mind is to apply the democratic norm. We can count how many studies get a risk with a significant p-value and in how many the value of p is non-significant (taking the arbitrary value of p=0.05).
Vote counting method
Good work, it seems a reasonable solution. We have two in favor and four against, so it seems clear that those “against” win, so we can quietly conclude that watching TV is not a risk factor for presenting bouts of dandruff. The problem is that we can be blundering, also quietly.
This is so because we are making a common mistake. When we do a hypothesis test we assume the null hypothesis that there is no effect. We always do the experiment and obtain a difference between the two groups, even by chance. So we calculate the probability of, by chance, finding a difference as we have obtained or greater. This is the value of p. If it is less than 0.05 (according to the usual convention) we say it is very unlikely to be due to chance, so the difference must be real.
In short, a statistically significant p indicates that the effect exists. The problem, and therein lies our mistake in the example we have set, is that otherwise is not met. If p is greater than 0.05 (not statistically significant) it could mean that the effect does not exist, but also that the effect does exist but the study does not have sufficient statistical power to detect it.
As we know, the power depends on the size of the effect and the size of the sample. Although the effect is large, it may not be statistically significant if the sample size is not large enough. So, faced with a p> 0.05 we cannot safely conclude that the effect is not real (we simply cannot reject the null hypothesis of no effect).
Given this, how are we going to make a vote counting how many studies are there for and how many against? Some of the cases of studies without significance could be due to lack of enough power and not because the effect doesn’t exist. In our example, we have four non-significant studies and two significant but, how can we be sure that the four non-significant mean absence of effect?. We have seen that we can’t.
We need a weighted result
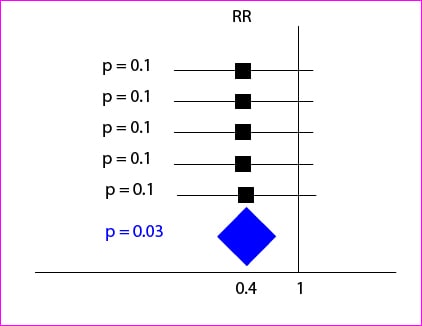
The right thing to do in these cases is applying techniques of meta-analysis and get a summary weighted value of all the studies in the review. Let’s see another example with the five studies depicted in the attached figure. Although the relative risks of the five studies show a protective effect (are less than 1, the null value) none reached statistical significance because their confidence intervals cross the zero value, which is the one for relative risks.
However, if we get a weighted sum, it has greater precision than individual studies, so that while the relative risk value is the same, the confidence interval is narrower and not cross the zero value: it is statistically significant.
Applying the method of the votes we could had concluded that there is no protective effect, while it seems likely that it exists when we apply the right method. In short, the voting method is unreliable and should not be used.
We’re leaving…
And that’s all for today. You see that democracy, although good in politics, is not so much when talking about statistics. We have not discussed anything about how we get the weighted sum of all the studies of the review. There are several methods applied in meta-analysis, including the fixed effect and the random effects model. But that’s another story…