Diagnostic threshold.

The other day I went to a costume party, one of those where everyone wears identical masks. You might think I would have a lot of fun, but the truth is that my happiness was marred by a small setback: finding my cousin, who I had arranged to meet there, among the crowd of masked people.

On the one hand, if I got the wrong person, I could end up greeting a stranger effusively (what an awkward moment!). I didn’t know whether to risk greeting anyone who looked even a little like my cousin so as not to miss the opportunity or wait until I was almost sure it was him, even if that meant risking not finding him, even if he was already there.

Does the situation sound familiar? It is, basically, the eternal struggle that we clinicians face between detecting patients in time and avoiding false positives.

Curiously, this tension between acting quickly or being cautious has marked historic decisions. During World War II, British radar operators faced a similar dilemma: identifying enemy aircraft in time (avoiding attacks) without alarming the population with false warnings. If they lowered the detection threshold too much, any flock of birds could be mistaken for German bombers. If they raised it too much, real attacks could go unnoticed. The balance was a matter of life or death.

And in the world of diagnostic testing, we faced a less dramatic, but equally uncomfortable version: choosing the optimal cut-off point on an ROC curve. Should we prioritize identifying all positive cases, even if that means accepting more false positives? Or be more conservative and reduce errors, even if we miss some true positives? In the end, as in the costume party or in the radars of war, it all depends on what is at stake.

The ROC curve

Let’s say, for example, that we develop a logistic regression model that gives us the probability that a subject is positive for a certain disease. In a similar case, we will face a key decision: at what cut-off point do we consider a result to be positive?

The first thing that occurs to us is to set this threshold at p = 0.5. Thus, if the probability is greater than or equal to 0.5, we classify the subject as positive; if it is less, as negative. However, this threshold is not always the most appropriate, especially when the categories are unbalanced (the probability of being healthy or sick is very different), in addition to not considering the clinical context, which can condition the greater or lesser risk of committing false negatives versus false positives.

For example, if we are diagnosing a rare disease such as the dreaded fildulastrosis, using p = 0.5 could lead to missing many real cases (low true positives and many false negatives), since the model will tend to classify them as negative. However, in situations where a false positive has serious consequences (such as a misdiagnosis that would lead to dangerous, bothersome, or very expensive treatments), we may want a higher threshold to minimize these errors.

This is where the Receiver Operating Characteristic curve (ROC curve) comes into play. This curve shows the overall performance of the test by plotting the sensitivity (true positives rate) against the false positive rate (1 – specificity) for different cutoff points.

The overall performance of the test is estimated by calculating the area under the curve (AUC). A perfect test would have a curve that passes through the upper left corner (where there would be 100% sensitivity and 0% false positives) and with an AUC = 1.

The problem is that perfect tests do not exist, so this maximum point, the so-called Youden point or index, is shifted down and to the right. We would think that the problem is solved: we will choose the cutoff point that marks the Youden index, where sensitivity and specificity are maximized. Well, this does not solve the problem in many cases either.

In practice, the optimal point depends on what we value most according to the clinical context in which we apply the diagnostic test. If we are interested in maximizing true positives (that almost no patient is left undiagnosed), we choose a lower probability threshold to consider the test result as positive. The cut-off point will move to the right of the curve, which will increase false positives.

On the other hand, if what we want is to reduce false positives, we raise the probability threshold, which will move the cut-off point to the left: lower sensitivity (we will miss undiagnosed patients) and fewer false positives.

The problem is finding the perfect threshold that gives us the balance we want, which can be especially complicated when the prevalence of the disease we want to diagnose is low, as we explained in a previous post.

The perfect threshold, or almost

In short, there is no universally optimal cut-off point, but each scenario requires adjusting the threshold based on the desired balance between sensitivity (Se) and specificity (Sp).

But don’t be fooled, the perfect threshold does not exist. There will always be a price to pay in false positives or negatives. Of course, we can haggle that price as we see fit. Let’s see this with a practical example.

We are going to play a bit with the cut-off points, using the freely access R program. If you want to see how I do the different calculations, you can download the script from this link.

For this example, I am going to use the Pima.te dataset, from the R MASS package. It contains a record of 332 pregnant women over 21 years of age who are evaluated for a diagnosis of gestational diabetes according to WHO criteria. In addition to the diabetes diagnosis (yes/no), it contains information on the number of pregnancies, plasma glucose, systolic blood pressure, triceps skinfold, body mass index, history of diabetes, and age.

In this data set there are 109 diabetics and 223 non-diabetics, which means a prevalence of gestational diabetes of 0.33.

The first thing we do is create a multiple logistic regression model with the diabetes diagnosis (1 = yes, 0 = no) as the dependent variable and the rest as independent variables. We are not going to ask ourselves if this is the best possible model, since it is not the subject of this post and, as we have described it, it serves us perfectly for what we want to show.

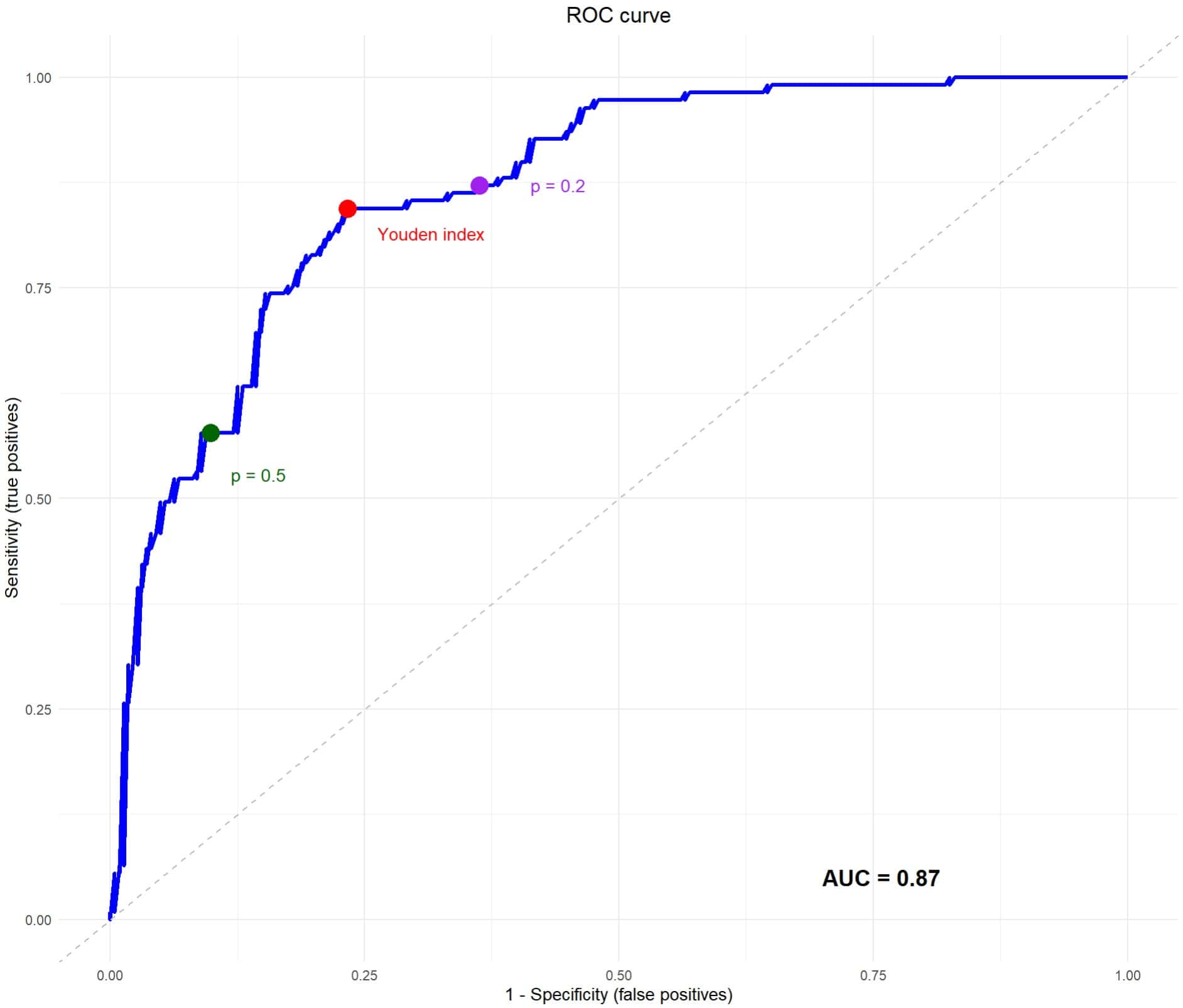
Once the model is created, the first thing we can do is estimate its overall performance by drawing the ROC curve and calculating the AUC, which you can see in the attached figure. Our calculation tells us that the test has an AUC = 0.87, which suggests that it performs well in discriminating between positive and negative results. Ignore, for the moment, the three points that appear on the curve, which we will discuss below.

The convenient threshold

Now we are ready to start haggling with our cut-off points. We are going to start with the default cut-off point of the logistic regression, which is usually to consider positive the one with a probability greater than or equal to 0.5 and negative the one with a probability less than this value. You can see this cut-off threshold represented on the ROC curve as a green dot.

The logistic regression model that we have built gives us the probability that each participant belongs to category 1 of the dependent variable or, more simply, that they are diabetic. If we choose the cut-off point p = 0.5, we will be marking this probability threshold of 0.5 to consider the test as positive (it will be negative if the probability is less than this value).

So, we go to the data set and look at who is or is not diabetic and what the model predicts if it considers as diabetic those who have a probability value of being so (according to the model) greater than or equal to 0.5. With this, we can calculate the contingency table and the values ​​of Se, Sp, true positives (TP), true negatives (TN), false positives (FP), false negatives (FN) and the diagnostic accuracy (the proportion of patients correctly classified). You can see this in the first table in the figure below.

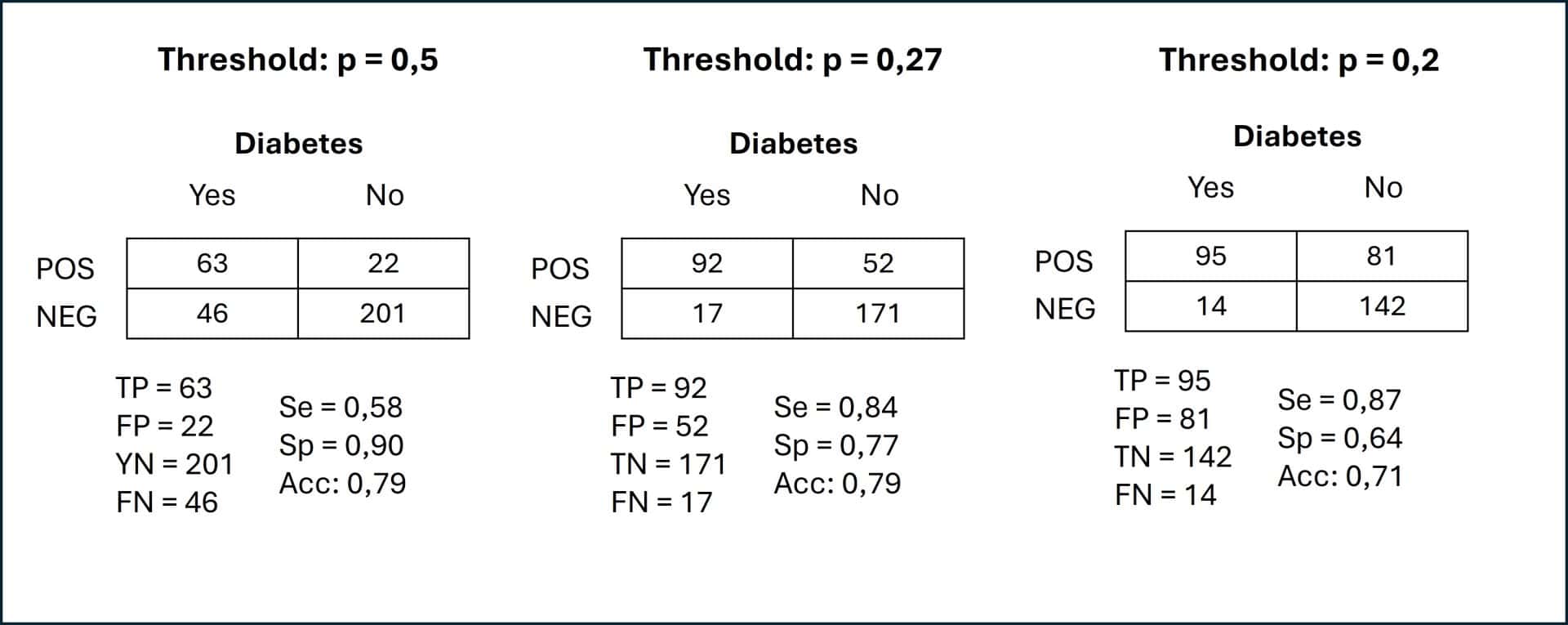
We can see that 79% of the patients are correctly diagnosed, with Se = 0.58 and Sp = 0.90. Although the diagnostic accuracy and Sp are not bad, the Se is a bit low for our taste, which translates into 46 pregnant women that we are going to leave undiagnosed and 22 false positive diagnoses.

I would say that this threshold does not suit us very much, but we could already imagine it. The prevalence of diabetes in the data set is 0.33, so this cut-off point penalizes the sensitivity of the test.

Let’s see what happens with the Youden point, which maximizes Se and Sp and which you see represented in the red curve as a red dot. This point would be equivalent to choosing a probability value greater than or equal to 0.27 to consider the result of the model as positive (category 1: diabetes). You can see the contingency table in the center of the figure above.

Since we have moved to the right on the ROC curve, we will expect an improvement in Se, with an increase in FP. Indeed, in the table we see an Se = 0.84, an Sp = 0.77 and a total of 52 FP. The good thing is that we are now only leaving 17 diabetic pregnant women undiagnosed (compared to 46 in the table above).

In my opinion, this cut-off threshold would be more appropriate for this scenario. I would say that it is worse to leave one diabetic undiagnosed than to have to perform the test to confirm the diagnosis in the FP (although this is a subjective criterion that depends on who has to establish the threshold).

Furthermore, leaving 17 diabetic pregnant women undiagnosed still seems like a lot to me, so I move a little further to the right of the curve and choose a probability threshold of 0.2, marked as a purple dot. Now look at the third contingency table.

As expected, the Se goes up a little, up to 0.87, and the FNs remain at only 14 total. The price to pay is an increase in the FPs up to 81. Risk, costs, etc. will have to be assessed, but I would say that between this and the Youden’s point would be the optimal threshold for this scenario.

We’re leaving…

And here we will leave the cut-off points for today.

We have seen how the choice of the cut-off point can significantly modify the performance of the same diagnostic test applied in the same clinical scenario.

Before saying goodbye,  I would like to reflect on a detail that I find interesting.

The ROC curve and the AUC represent the overall performance of the test to correctly classify sick and healthy people. If you notice, we have only calculated one AUC, even though we have calculated multiple Se and Sp values ​​for different cut-off points. In addition, the diagnostic accuracy is practically the same for all cut-off points (there are small differences due to rounding errors).

This is logical, because these parameters indicate the overall performance and are not the only ones to take into account when choosing the usefulness of a certain test in a specific scenario. It may happen that curves with a high AUC have a lower performance in some scenarios, especially when the prevalence of the disease to be diagnosed is very low.

But this is no reason to dismiss the test without further ado. We can always play with the cut-off probability threshold to adapt the performance to our interests and apply some other tool for these cases of very unbalanced diagnostic categories, such as the precision enrichment ratio. But that is another story…