Quality of a linear regression model.

The parameters that report on the quality of a linear regression model and that are usually provided by the statistical programs with which they are carried out are reviewed. Emphasis is placed on the goodness of fit, the predictive capacity and the statistical significance of the model.
It is incredible the turns that our mind can take when we let it wander as it pleases. Without going any further, the other day I asked myself a question that I find truly disconcerting: why do people insist on wearing different colored socks?
Surely it has happened to you at some time. No matter how carefully we select our clothes in the morning, there always seems to be a mischievous goblin that makes fun of our coordination. Some might argue that it’s simply an expression of bold and mindless creativity, while others believe it’s a global conspiracy to keep us all slightly off balance.
But today we are not going to talk about my mental delusions about the colour of the socks. And it is that in this world where fashion and chaos are intertwined in an inexplicable dance, we find ourselves with an even greater challenge: understanding and evaluating the quality of a multiple linear regression model.
That’s how it is. Just as we look for harmony in our clothing ensembles, we also long for a regression model that fits precisely and gives us reliable results. How can we distinguish between a mediocre model and one that stands out in terms of quality parameters? Follow me on this journey, where we’ll explore the secrets behind coefficients and discover how to measure excellence in the realm of multiple linear regression.
Multiple linear regression model
We have already seen in previous posts how regression models try to predict the value of a dependent variable knowing the value of one or more independent or predictor variables. In the case of one independent variable, we will talk about simple regression, while if there is more than one, we will deal with multiple regression. Finally, let’s remember that there are different types of regression depending on the type of variable that we want to predict.
Today we are going to focus on multiple linear regression, whose general equation is the following:
Y = b0 + b1X1 + b2X2 + … + bnXn
In which, Y is the value of the dependent variable measured on a continuous scale, b0 is the constant of the model (equivalent to the value of the independent variable when all the dependent variables are zero or when there is no effect of the independent variables on the dependent one), bi the coefficients of each independent variable (equivalent to the change in the value of Y for each unit of change in Xi) and Xi are the independent variables.
We also saw in a previous post how the linear regression model requires that a series of requirements be met for its correct application.
These are the assumption of linearity (the relationship between the dependent and independent variables must be linear), the assumption of homoscedasticity of the model residuals (the differences between the observed values and those predicted by the model must follow a normal distribution with equal variance throughout all the values of the variables), the assumption of normality of the residuals and, finally, one specific to multiple regression, that there is no collinearity (that there are no independent variables correlated with each other).
Usually, we use statistical programs to create regression models, since it is unthinkable to do them manually. The problem is, sometimes, in assessing the large amount of information about the model that the program calculates and shows us.
This is so because there are several key aspects that we must assess to determine its quality and validity. One of them is the goodness of fit, which tells us how well the observed data fits the model predictions.
In addition, we must consider the predictive capacity of the model, evaluating its ability to generalize and accurately predict new values. Another important aspect is the statistical significance of the regression coefficients, which allows us to determine if the independent variables have an informative effect on the dependent variable.
In summary, when analysing a multiple linear regression model, we must consider the goodness of fit, the predictive capacity and the statistical significance of the coefficients to obtain solid and reliable conclusions, so it is essential to know the parameters that inform us about the quality of the model.
A practical example
To develop everything we have said so far, we are going to use an example made with a specific statistical program, the R program. We are going to create a multiple linear regression model and analyze all the results that the program generates about the model.
As is logical, the output of results will vary depending on the statistical program that we use, but basically, we will have to analyze the same parameters regardless of which one we use.
We are going to use the “iris” dataset, which is frequently used for teaching with R, which contains 150 records with measurements of petal length and width (“Petal.Length”, “Petal.Width”) and sepals (“Sepal.Length”, “Sepal.Width”) of three flower species (“Species”): setosa, versicolor and virginica.
Suppose we want to predict the petal length (“Petal.Length”) using the independent variables “Sepal.Length”, “Sepal.Width”, “Petal.Width”, and “Species”.
To do this, we use the “lm()” function to fit the multiple linear regression model. The formula must specify that Petal Length (“Petal.Length”) is the dependent variable, while “Sepal.Length”, “Sepal.Width”, “Petal.Width”, and “Species” are the independent variables:
model <- lm(Petal.Length ~ Sepal.Length + Sepal.Width + Petal.Width + Species, data = iris)
The model is stored in a variable called “model”. To view the available information, the easiest way is to run the summary(model) command. You can see the result in the attached figure, which includes information on the coefficients, the statistical significance, and the goodness of fit of the model.
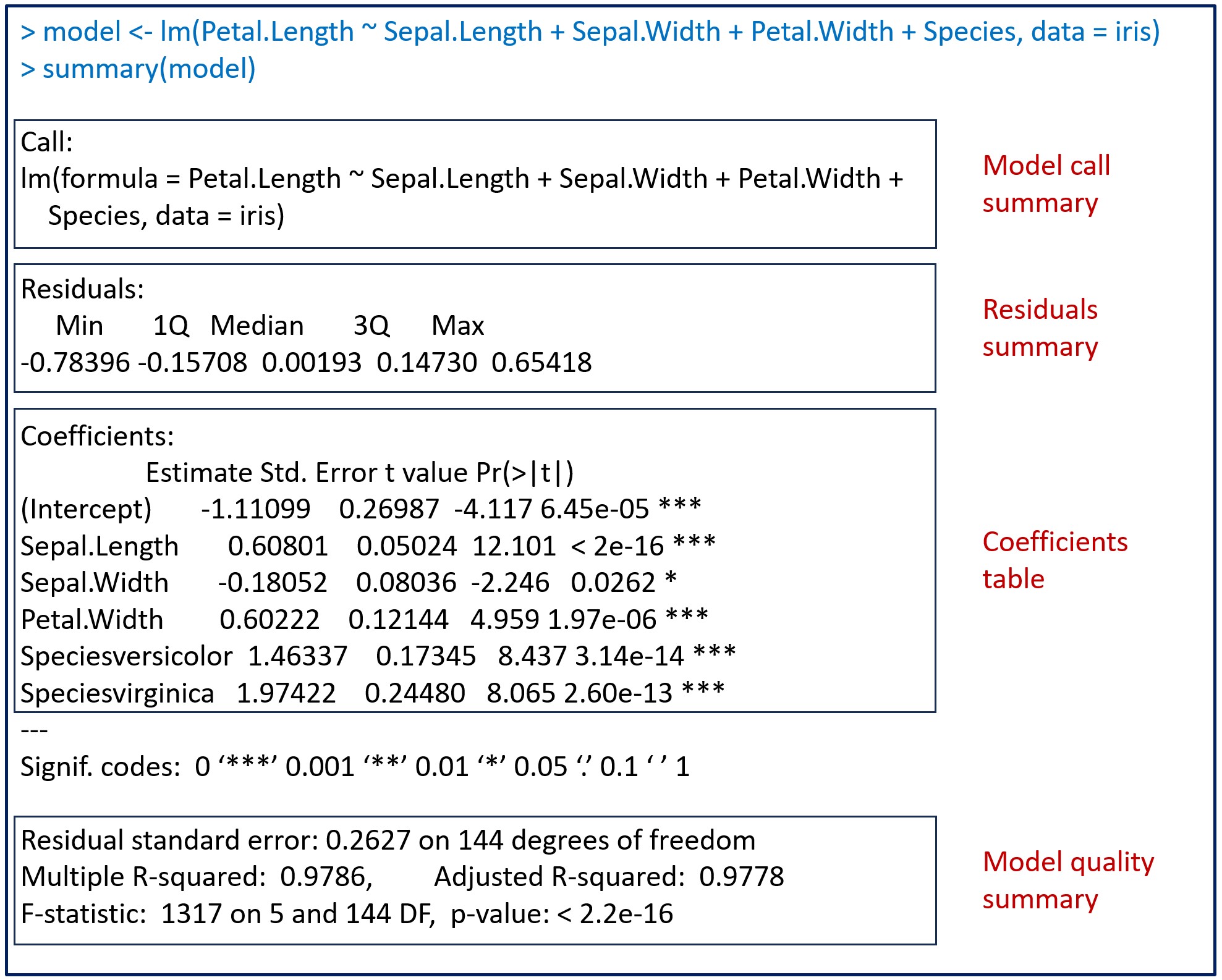
In the figure, I have added some boxes to separate the different aspects of the model information that R provides. Let’s see them one by one.
Model call summary
The first thing the summary() function shows is the formula used to build the model. This is the time to check that the formula is correct, that we have included in the model all the independent variables that we want, and that we have used the appropriate data set.
According to R syntax, the lm() function includes the formula with the dependent variable to the left of the “~” symbol and the sum of the independent variables to its right. Finally, it specifies that we have used the data from the “iris” set.
Residuals summary
Next, we have the summary of the residuals of the regression model. We already know that the residuals are the prediction errors of the model or, what is the same, the difference between the real values and those predicted by the model, so it is easy to understand that they are very important data to assess the quality of model fit.
The most common way to calculate the values of the regression coefficients of the model is the so-called least squares method, which looks for the minimum value of the sum of the squares of the residuals. In this way, what interests us is that the value of the residuals is as low as possible (that there are minimal differences among the real values and those predicted by the model).
The program provides us with the maximum and minimum values of the residuals, in addition to the three quartiles: the first quartile (the upper bound of the 25% of the residuals ordered from smallest to largest), the median or second quartile (which leaves each side 50% of the residuals) and the third quartile (the upper bound of 75% of the residuals).
The distribution of the residuals in the quartiles gives us an idea of the distribution of the data. For the assumption of normality of the residuals to be fulfilled, the median must be close to zero and the first and third quartiles must be equidistant from the median (and with as low a value as possible).
In our case, the median is practically 0 and there is a symmetric distribution of the first and third quartiles, with values not very high. Notice the interest that these two quartiles have, since they define the range of 50% of the residuals of the model. If we take a random prediction, the residual will be between -0.157 and 0.147 half of the times. This will be the frequent magnitude of the error of the model, which can already give us information about whether it is too large to be able to apply it to our practice.
The coefficients table
We now focus on the table of the regression coefficients of the model, which is a matrix with the coefficients in the rows and a series of columns:
- Name of the variable.
- Estimated value of the regression coefficient (estimate).
- The standard error of the coefficient (Std. Error), which allows us to calculate its confidence interval.
- The measure of statistical significance of each estimated coefficient, in the form of a t-value. The t-value is calculated by dividing the estimated value of the coefficient by its standard error. It provides an indication of how many standard deviations the estimated coefficient is away from zero (the null hypothesis assumption is that the coefficients are not different from 0). In general, the larger the absolute value of the t-value, the more significant the coefficient.
- The p-value (Pr(>|t|)), which tells us the probability of finding a value of t so far from or more than 0 by chance alone. As we already know, it is usual to consider this difference as statistically significant when p < 0.05.
This value can be distorted if there is collinearity, which can even cause the loss of statistical significance of the coefficient of a variable that does intervene in the adjustment capacity of the model.
A clue that can make us suspect that there is collinearity is the presence of abnormally large coefficients in comparison with the others, with the opposite sign to what it would seem to us that it should have due to our knowledge of the context in which the model is applied, or with a very high standard error. Logically, all this assumes that we have previously verified that the assumption of normality of the residuals is fulfilled, as we have already mentioned.
In these cases, the global model can even make correct predictions, but our interpretation of which variables contribute the most to its explanatory power can be distorted by the presence of correlated independent variables.
Let’s take a look at our coefficients. We have the intercept and 5 independent variables, the three quantitative (Sepal.Length, Sepal.Width and Petal.Width) and two coefficients for the “Species” variable.
The variable “Species” is a qualitative one with 3 categories: setosa, versicolor and virginica. What the program has done is take the setosa as a reference (the first category in alphabetical order) and create two indicator or dummies variables: “Speciesversicolor” (value 1 if the species is versicolor) and “Speciesvirginica” (value 1 if the species is virginica).
We see that all the coefficients, including the intercept, have p values < 0.05, so they are all statistically significant. Do not be tempted to consider those with the lowest p-values to be the best coefficients. Once the value of p is below the threshold that, by consensus, we consider significant, we do not care how small it is.
Thus, our regression equation would be as follows:
Petal.Length = -1.11 + 0.60xSepal.Length – 0.18xSepal.Width + 0.60xPetal.Width + 1.46xSpeciesversicolor + 1.97xSpeciesvirginica
The meaning of quantitative variables is easier to interpret. For example, 0.60xSepal.Length means that, holding all other variables constant, each unit increase in sepal length contributes 0.6 unit increase in petal length (the dependent variable).
For the same value of the independent quantitative variables, a vesicolor flower will have a petal length 1.46 units greater. On the other hand, if the flower is a virginica, this increase in the length of the petal will be 1.97 units.
Model quality summary
The last part of the output of the summary() function shows us the quality statistics of the global model. It is very important to check the quality of the parameters in this section before applying the model and not rely solely on the statistical significance of the regression coefficients.
The parameters that we must assess are the following:
1. The degrees of freedom. The number of degrees of freedom of the model is calculated by subtracting the number of model coefficients from the number of observations. In our example we have 150 observations and 6 coefficients, so the model has 144 degrees of freedom.
If you pay attention, the degrees of freedom inform us of the relationship between the number of observations and the number of independent variables that we introduce in the model. As is logical, we will be interested in the number of degrees of freedom being as high as possible, since a low number would indicate that the model may be too complex for the amount of data we have, with which the risk of overfitting the model will be very high.
2. Residual standard error. It is the sum of the squares of the residuals divided by the number of degrees of freedom. It is similar to the sum of squares of the residuals used by the least squares method but adjusted for the sample size by dividing it by the degrees of freedom.
Using the standard error of the residuals and not their sum of squares is another attempt to adjust the parameter according to the complexity of the model. Higher values will indicate more complex models (fewer degrees of freedom and, therefore, a greater number of independent variables with respect to the number of observations) that will have a greater risk of overfitting and a worse ability to generalize predictions.
3. R2 multiple and adjusted. R2, or coefficient of determination, is another important measure of the goodness of fit of the model. This parameter explains the total variance of the data set that the model is able to explain. Let’s see a simple way to calculate it to better understand its meaning.
Going back to our example data, any prediction model we develop will have to perform better than what statisticians call the null model. In this case, the null model would be represented by the mean length of the petals of all the flowers in our sample. Thus, a simple estimate would be to predict that a randomly chosen flower has a petal length equal to this mean value.
This estimate is very simple, but it will also be very inaccurate (the more so the greater the variability there is in the size of the flowers). In any case, even if the null model is not very good, we take it as a reference to beat with the models that we can develop.
If we calculate the sum of the squares of the residuals of the null model, we will obtain the so-called total sum of squares (SST), which is the total variance of the data that we are studying.
What we want is to develop a model whose sum of squares of residuals (SSR) is much smaller than the total variance (SST). This is the same as saying that we want the ratio between SSR and SST to be as small as possible (as close to 0 as possible). To be able to interpret it more easily, we calculate the coefficient of determination as the complement of this quotient, according to the simple equation that I show you below:
R2 = 1 – (SSR / SST)
Therefore, R2 compares the variance of our model with the total variance of the data, so it informs us of the percentage of variability of the data that the model explains. Its value can range from 0 (the worst model) to 1 (a model with a perfect fit).
But the coefficient of determination has a small drawback: if we greatly increase the number of independent variables in the model, the value of the coefficient is magnified even though the variables are not very informative.
If you think about it, this is the same problem that we have already assessed several times. More complex models tend to perform better because they tend to overfit the data, but they will generalize worse when we later apply the model to our environment.
For this reason, the so-called adjusted coefficient of determination is calculated, which is a more conservative estimator than R2 of the model’s goodness of fit. In addition, it can be used to compare the goodness of fit when comparing models with a different number of independent or predictor variables made from the same data.
The formula, for those addicted to mathematics, is as follows:
Adjusted R² = 1 – [(1 – R²) x (n – 1) / (n – p – 1)],
where n is the number of observations and p the number of independent variables.
If you look at our example, the values of the two coefficients are very similar, but that’s because we’re using a fairly simple model. With more numerous data and a high number of independent variables, this difference tends to become more striking.
4. The significance of the model. The information from the summary() function ends with the test on the statistical significance of the global model.
In the same way that the t-values were used to calculate the statistical significance of the regression coefficients of the model, Snedecor’s F is used to test the significance of the global model.
As we already know, F compares the ratio of two variances. In this case, the variance of the residuals of the null model versus the variance of the residuals of our model, which we want to be as different as possible. Using the p-value, the program estimates the probability that we will observe an F statistic as large or greater than that observed under the null hypothesis assumption that the numerator and denominator are equal (F = 1).
It goes without saying that we are interested in it being less than the value chosen as the threshold for statistical significance which, by convention, is usually p < 0.05. In this case, the model is statistically significant.
To finish, just mention that the fact that the model is statistically significant does not mean that it fits the data well, but simply that it is capable of predicting better than the null model. Sometimes a model with a significant F and a low R2 value will tell us that, although the model works better than the null, its ability to make predictions (its goodness of fit) is not good enough. Surely there are, in similar cases, more variables involved in the behaviour of the data and that we have not included in the model (although it may also happen that the type of model chosen is not the most adequate to explain our data).
We are leaving…
And here we will leave it for today.
We have seen how to correctly read and interpret all the information on the goodness of fit and the quality of the multiple linear regression models provided by computer programs.
Logically, and as we have already commented, all this must be completed with a correct diagnosis of the model to verify that the necessary assumptions for its application are met.
We have also discussed how the existence of multicollinearity among the independent variables can bias the value of the coefficients and make it difficult to interpret the model. In these cases, the ideal will be not to introduce correlated variables and simplify the model. But this is not always easy or convenient. For these situations we can count on the so-called linear regression regularization techniques, such as lasso regression or ridge regression. But that is another story…
