Analysis of logistic regression models.

Ah, the mysterious and capricious air! A born troublemaker who perplexes us with his paradoxical antics. At home, it is the eternal enemy of our plans to stay healthy. A slight draft of air is enough to transform us into trembling beings with colds. It’s like the air is conspiring with the tissues to stay in business.
But wait! When we get to the beach, the air becomes our tanning ally. Each burst plays at being a skillful artist who gilds our skin under the sun. It seems the air changes his personality like a chameleon, going from icy Dr. Jekyll at home to toasty Mr. Hyde on the beach. Could it be that the air has a double life? Who’d say!
And so, dear friends, while the air continues with its game of contrasts, today we are going to delve into the analysis of multiple logistic regression models. Although in this case we will not find mysterious paradoxes, we will discover the magic of how this statistical tool can help us evaluate and assess the quality of predictive models.
Once again, we will try to see what is necessary to know if a predictive model can be able to convert uncertainty into precision.
Multiple Logistic Regression Model
We have already seen in previous posts how regression models try to predict the value of a dependent variable knowing the value of one or more independent or predictor variables.
Today we are going to focus on multiple logistic regression, whose general equation is the following:
ln( Odds Y ) = b 0 + b 1 X 1 + b 2 X 2 + … + b n X n ,
where Y is the value of the binary dependent variable, b 0 is the constant of the model (equivalent to the value of the dependent variable when all the independent variables are zero or when there is no effect of the independent variables on the dependent one), bi the coefficients of each independent variable (they represent the change in the probability of the event of interest occurring for each unit of change in the independent variable Xi ) and Xi theindependent variables.
The binary dependent variable can be any event that does or does not occur, such as winning or not winning the lottery. Independent variables can be any characteristic of the subjects that is believed to be related to the dependent variable, such as whether you play the lottery or not, how much you play, how often and if you are a jinx or a lucky person.
The probability is estimated using a logistic function, which is a function that maps real values to the range [0, 1]. If we calculate the natural antilogarithm (or, what is the same, we apply the exponential function) we will obtain the odds of the occurrence of the event labeled as 1. Now, we only have to calculate the probability from the following formula:
P = Odds / ( Odds + 1)
A practical example
To explain how to interpret the results of a logistic regression model, we are going to use an example made with a specific statistical program, the R program. We are going to create a multiple logistic regression model and analyze all the results that the program offers us about the model.
As is logical, the output of results will vary depending on the statistical program that we use, but basically we will have to analyze the same parameters regardless of which one we use.
So that you can replicate what I am going to tell you, I’ll use the “Melanoma” data set, included in the R package “MASS”. This set contains data from 205 patients with melanoma and includes a series of variables: survival time in days (time), survival status (status , coded as 1: death from melanoma, 2: alive, 3: death from another cause), gender (sex , coded as 1: male, 0: female), age in years (age), year of the intervention (year), tumor thickness in millimeters (thickness) and presence of ulceration in the tumor (ulcer , coded as 1 : presence , 0 : absence).
The first thing we will do, once R is launched, is to install the package, if we have not done it previously. Then we load the MASS library and the data set:
install.packages("MASS")
library(MASS)
data(Melanoma)
This is a survival study but, for simplicity, we are going to omit the censored data and the time in which the event occurs (status). In addition, we are going to transform the status variable into a dichotomous one coded as 1 if death from melanoma has occurred and 0 if he is alive or died from another cause (not died from melanoma). We use the following command:
Melanoma$status <- ifelse(Melanoma$status == 1, 1, 0)
Once we have the data prepared, we are going to try to find out which of the variables collected in the registry influence the probability of death from melanoma, either increasing or decreasing it, and to what degree they do so. To do this, we build the multiple logistic regression model, according to the following command:
model <- glm(status ~ time + sex + age + year + thickness + ulcer, data = Melanoma, family = binomial(link = "logit"))
The model is stored in a variable called “model”. To view the available information, the easiest way is to run the summary(model) command. You can see the result in the attached figure, which includes information on the coefficients, statistical significance, quality and goodness of fit of the model.
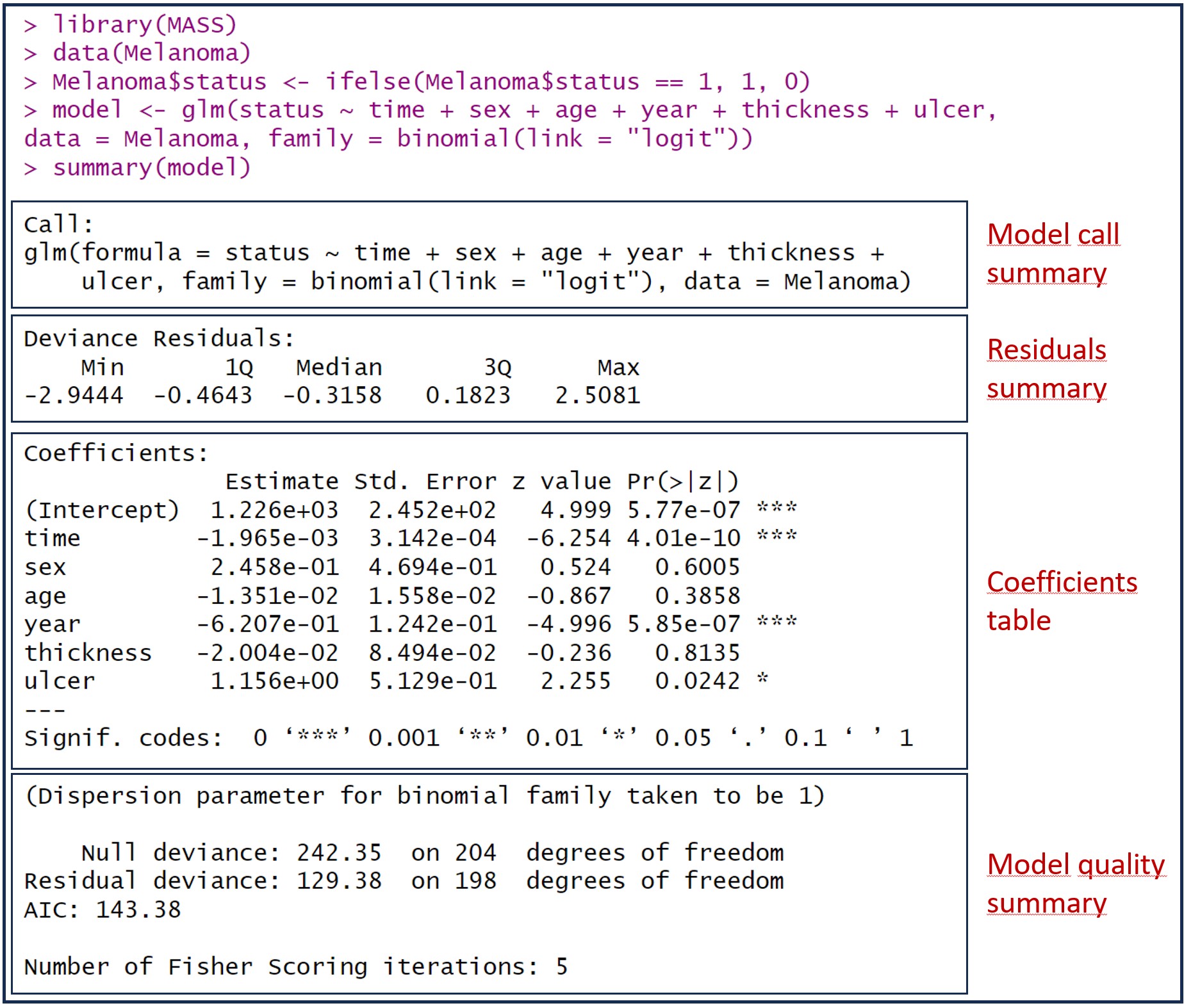
In the figure I have added some boxes to separate the different aspects of the model information that R provides us. Let’s see them one by one.
Model construction
The first thing the summary() function shows us is the formula used to build the model. This is the time to check that the formula is correct, that we have included in the model all the independent variables that we want, and that we have used the appropriate data set.
According to R syntax, the glm() function includes the formula with the dependent variable to the left of the “~” symbol and the sum of the independent variables to its right. Next, the data set used is specified. Further to the right, the term family specifies the distribution that we assume follows the dependent variable, which in this case is a binomial. Finally, the link function is established, which is used to convert the dependent variable into a scale that is easier to work with. The most common link function for logistic regression is the logit function, which takes the value of the dependent variable (any real value) and converts it to a probability between 0 and 1.
Summary of deviance residuals
Deviance residuals, also called Pearson’s residuals, are the analogue of linear regression model residuals and reflect the differences among the actual values of the dependent variable and the values predicted by the model. The difference is that the dependent variable in linear regression is continuous, whereas in logistic regression it is binary, so the calculation of deviance residuals is based on log-likelihood rather than the sum-of-squares-of-errors method.
Let’s make a small aside for those who don’t quite understand what this log-likelihood thing means.
Likelihood is a measure of the probability of observing a data set given a set of parameters in the model. Usually, it is easier to work with logarithms, calculating the log-likelihood as the sum of the logarithms of the probabilities of obtaining each real observed data, given the parameters of the model. Its formula, for lovers of strong emotions, is as follows:
L(β) = ∑ [y_i * log(p_i) + (1 – y_i) * log(1 – p_i)]
Don’t be scared, it’s actually not as unfriendly as it seems. L(β) represents the log-likelihood function, which we will want to be as large as possible (best fit of the model). y_i represents the value of the dependent variable for observation i, and p_i is the model-estimated probability of the event of interest occurring (coded as 1 on the dependent variable).
The goal in logistic regression is to find the optimal values of the β parameters that maximize the log-likelihood function (the model fits better the observed data), which is done by the maximum likelihood algorithm.
With that said, let’s get back to our residuals. We see that the program gives us the maximum and minimum values, in addition to the three quartiles: the first quartile (the upper limit of 25% of the residuals ordered from smallest to largest), the median or second quartile (leaving 50% of the residuals on each side), and the third quartile (upper limit of 75% of the residuals).
The assessment of the distribution of the residuals is also somewhat different from that of linear regression. Although the mean of the residuals is not necessarily zero, a median close to zero does indicate that the residuals are symmetrically distributed around zero and that the model has good predictive power.
On the other hand, although it partly depends on the context of application of the model, a more negative value of the first quartile suggests that the model is overestimating the probability of the event of interest occurring (dependent variable coded as 1). Similarly, a more positive third quartile value suggests that the model is underestimating the probability of the event of interest occurring. Furthermore, the greater the difference between the first and third quartiles (greater interquartile range), the less precision the model will have.
In summary, we are interested in obtaining a model with a median of the residuals close to zero and symmetrically distributed to have a better predictive capacity. The more centered around zero, the more accurate the predictions are.
If we apply what has been said to our example, it seems that the model does not have a very good predictive capacity and that it probably overestimates the probability of the event of interest, mortality from melanoma, occurring.
The coefficient table
After the distribution of the residuals, we are shown the table of the regression coefficients of the model, with the coefficients in the rows and a series of columns:
1. Name of the variable.
2. Estimated value of the regression coefficient (estimate).
3. The standard error of the coefficient (Std . Error), which allows us to calculate its confidence interval.
4. The measure of statistical significance of each estimated coefficient, in the form of z-value. The z-value is calculated by dividing the estimated value of the coefficient by its standard error. It provides an indication of how many standard deviations the estimated coefficient is away from zero (the null hypothesis assumption is that the coefficients are not different from 0). In general, the larger the absolute value of the z-value, the more significant the coefficient.
5. The value of p ( Pr(>|z|) ) , which tells us the probability of finding a value of z so far or more than 0 by chance alone. As we already know, it is usual to consider this difference as statistically significant when p < 0.05.
Those coefficients that are statistically significant correspond to the variables that contribute to explain the variability of the model. Those with a negative value are negatively correlated with the odds (and therefore with the probability) of the event of interest occurring. In turn, the positives do so in a positive way.
As with linear regression, the regression coefficients can be biased by the presence of collinearity. A clue that can lead us to suspect that there is collinearity is the presence of abnormally large coefficients compared to the others, with the opposite sign to what it would seem to us that it should have (based on our knowledge of the context in which the model is applied), or with a very high standard error.
The interpretation of logistic regression coefficients is a bit more complicated than that of linear regression, as they represent the change in the natural logarithm of the odds ratio (OR) of an event occurring (the category 1 dependent variable) in response to a unit change in the independent variable of the coefficient, holding the other independent variables in the model constant . Stated more precisely, although perhaps less understandable, it represents the change in log-likelihood for each unit increase in the independent variable to which the coefficient corresponds.
Therefore, to calculate the OR of a variable we will have to apply the exponential function (the natural anti-logarithm) to the regression coefficient of that variable (which only makes sense if it is statistically significant).
Let’s take a look at our model. We have the intercept and 6 independent variables, but only the intercept, the survival time in days (time), the year of the intervention (year) and the presence of ulceration in the tumor (ulcer , coded as 1: presence, 0: absence) reach statistical significance.
Survival time in days, a quantitative variable, has a correlation coefficient of -0.001965. If we apply the exponential function (exp( -0.001965)) we obtain an OR of 0.998. As we can see, a negative coefficient (which is equivalent to an OR < 1) indicates that the variable decreases the probability of the event (death from melanoma) occurring. Furthermore, it is statistically significant, so it seems that survival time is an important variable. What is the problem?
The problem is that those very small coefficients will give us ORs close to 1, the null value of the OR. In general, an OR close to 1 suggests that the variable is not a strong predictor of the event of interest and that its effect on probability is practically negligible. In this case, the variable may not be relevant to the model, and its inclusion may not provide much information or improve the predictive capacity, even if it is statistically significant.
Of course, all this must be seen in context. Due to the logarithmic nature of the logistic regression model, the magnitude of the survival effect in days may be more important when the value of the number of days is larger. If time is coded in months instead of days, the coefficient will remain the same in log-likelihood terms, but the interpretation of the associated OR will change based on the new scale.
Let’s see the interpretation of the effect of the ulceration variable (ulcer). Its coefficient is 1.156, whose exponential (OR) is 3.18. Being a positive coefficient, it will give us an OR > 1, so its presence (the value coded as 1) increases the risk of death from melanoma. Specifically, it is about 3 times more likely to die from melanoma when it is ulcerated than when it is not.
Model quality summary
The last part of the output of the summary() function shows us the quality statistics of the global model. It is very important to check the quality of the indicators in this section before applying the model and not rely solely on the statistical significance of the regression coefficients.
First, R gives us a message about the dispersion of the binomial function, which it has set to 1. Let’s see what this means.
We have assumed that the dependent variable follows a binomial distribution (death from melanoma or no death from melanoma) and we have used the logit link-functionto model the probabilities of the event of interest occurring. Well, for the binomial family it is assumed that the dispersion is constant and that the data fit the model properly, which implies that the variance of the binomial distribution remains constant throughout the range of values predicted by the model.
When the dispersion is set to 1, it means that the variance of the data fits the standard binomial model well. If there was overdispersion (variance greater than 1) or under-dispersion (variance less than 1), the value of the dispersion parameter would be adjusted accordingly to reflect such additional or reduced variability. So what R is telling us is that the variance fits the standard binomial logistic regression model well.
Following this comment on dispersion, a series of parameters that we have to assess are shown:
1. Null and residual deviances. These are two measures that help us to assess the goodness of fit of the model and compare its predictive capacity with that of the so-called null model, which would be the one that only contains the intercept term and does not consider any explanatory or independent variable to predict the dependent variable.
If we think about it a bit, this means that all the observations would be grouped into a single category of the dependent variable. This allows the null model to serve as a benchmark for comparing the performance of more complex models that include independent variables.
Deviance represents the differences between the model predictions and the actual observed value of the independent variable. The null deviation represents the discrepancies when the null model is fitted, while the residual deviation is the one obtained with the model in which we include the independent or predictor variables.
If we compare the residual deviance of our model with the deviance of the null model, we can see that the deviance decreases, indicating that the predictive power of the model is improved. In our example, the residual deviation is 129.38, less than that obtained with the null value, 242.35.
This can also be used to compare several models, so that the one with the smallest deviation will fit the data better.
Another utility of these parameters is that they allow us to calculate a pseudo-R2 , with a similar meaning to the coefficient of determination of linear regression. We can calculate it according to the following formula:
pseudo-R 2 = 1 – (model deviation / null model deviation)
In our case, it would have a value of 1 – (129.38 / 242.35) = 0.46. The interpretation is similar to that made in linear regression: the model explains 46% of the total variance of the dependent variable.
2. The degrees of freedom. As in linear regression, they give information on the amount of information available that is used to estimate the model parameters. In other words, they inform us of the complexity of the model, which will influence the goodness of fit and the ability to generalize the model with data other than those used for its calculation.
The degrees of freedom of the null model are calculated as the number of observations minus 1. In our example, 205 – 1 = 204. Those of our model are obtained by subtracting the number of model coefficients from the number of observations: 205 – 7 = 198.
A low number of degrees of freedom may indicate excessive model complexity. If we compare several models, in general we will prefer those with more degrees of freedom. Remember that the most complex models are the ones with the greatest risk of overfitting.
Finally, the degrees of freedom and the values of the deviations allow us to calculate the overall statistical significance of the model (which is the same as saying that to calculate if the difference between our model and the null model is statistically significant).
This is similar to the value of F that is calculated in linear regression. In the case of logistic regression we use the chi-square to calculate the so-called residual chi-square:
residual chi-square = zero deviance – residual deviance
This value, (in our example, 242.35 – 129.38 = 112.97) follows a chi-square distribution with a number of degrees of freedom calculated by subtracting the degrees of freedom of residual deviance from that of the null model deviance. In our example it would be 204 – 198 = 6. We can now go to R and calculate the p-value for this residual chi-square value:
1 - pchisq(112.97, 6)
We see that the value of p is practically zero: our model is statistically significant. In any case, it is worth remembering that the fact that the model is statistically significant does not mean that it fits the data well, but simply that it is capable of predicting better than the null model.
Sometimes, a significant model with a low pseudo-R2 value (or high deviation) will tell us that, although the model performs better than the null model, its ability to make predictions (its goodness of fit) is not quite good. Surely there are, in similar cases, more variables involved in the behavior of the data and that we have not included in the model (although it may also happen that the type of model chosen is not the most adequate to explain our data).
3. The Akaike Information Criterion (AIC). It represents the log-likelihood adjusted by the number of coefficients in the model. This is similar to how the coefficient of determination of linear regression is fitted and reflects, in some ways, the complexity of the model.
The AIC allows you to compare several models that use different predictor variables. In general, we will prefer the model with the lowest AIC, since its goodness-of-fit and ability to generalize its application is likely to be the best (less risk of overfitting).
4. Number of Fisher scoring iterations.
At the end of the model summary we find the number of Fisher scoringiterations algorithm.
Simply explained, it is an algorithm that tries to find the maximum likelihood estimators of the model. The algorithm starts working and iterates until the model coefficients converge, which means that substantial changes in the parameters are no longer observed with new iterations, thus finding the coefficients that maximize the likelihood function.
Convergence is expected to occur after 6-8 iterations. When the number is higher, it means that there may not have been convergence, which makes the model less valid. In our example, the number of iterations is 5, within what is considered adequate.
Fisher’s method is widely used, but you can also find another, such as Newton-Raphson’s.
We’re leaving…
And with this we end this long post, but the thing is that logistic regression has a lot to do with it. Actually, as much as being able to demonstrate that you can catch a cold or get tanned by the action of the air.
We have reviewed how to assess the summary of a logistic regression model, using a set of data for which I am not responsible from a medical point of view. Let no one draw conclusions about melanoma based on these data.
We have skipped over the last part, the convergence of the model. What happens when there is no convergence? Can we do anything to remedy the problem?
One of the causes may be that there is what is called separation or quasi-separation, which occurs when one or several independent variables are able to predict the dependent variable very well for a subset of the data available to develop the model. It’s funny, but logistic regression can perform worse if one of the variables is “too good.”
Although there is no need to despair. We can always try to minimize the problem by resorting to regression regularization techniques. But that’s another story…
