Sample size for the comparison of two means.

We saw in a previous post how we could estimate the mean value of a random variable, such as the level of cholesterol in blood, in a population without having to measure cholesterol levels of all the individuals in the population.

To do this, we selected a representative sample of individuals from the population and measured their cholesterol, obtaining the mean in the sample. Then, from that mean, we could already estimate between what values the mean value of the population, which is unattainable for us, could be found.

The key question was how many individuals we had to include in the sample. We have already seen how the necessary number depended on the confidence level with which we wanted to make the estimate, its precision and the variability of the variable in the population.

Comparison of two means

In the previous case we estimated the value of a continuous variable in a population from its value in the selected sample.

Now let us think that the characteristics of that variable can be differentiated according to the categories of another variable. For example, suppose we want to know if the mean cholesterol values are the same in boys and girls.

In this case we should select two samples, one for girls and one for boys, calculate the mean cholesterol values in the two samples and compare them to see if the difference we observe between the determinations may be due to chance. For this we can use several tests, such as the Student’s t test, which will even work well even if the sample is not very large and we do not know the variance of the variable in the population.

But how many boys and how many girls will we have to select? Keep reading and you will see.

Sample size for the comparison of two means

There are several factors that will influence the sample size needed to compare two means. In the first place, we will have to decide if it is enough for us to find out that the two means are different or if we want to specify if one of them is greater or less than the other. That is, we must define the direction of the contrast, unilateral or bilateral.

In addition, we need to set the confidence level and power that we want, and the size of the difference between the two means that we want to be able to detect statistically. Finally, we need to know the value of the variance of the variable in the two groups in the population.

Let’s look at each of these factors.

Unilateral or bilateral contrast

Even if it is just by chance, surely when we calculate the mean values of the two samples we will obtain different results.

We will be interested, when we go to test the null hypotheses, to know what is the probability that this difference is due to chance. If it is very high, we will assume that the two means are equal and the observed difference is due to chance. If it is very low (usually <0.05), we will assume that there is a difference that is probably not due to chance (the difference will be statistically significant).

At this point, we will decide if it is enough for us to know that the means are different or if we want to determine if one of them is specifically higher or lower than the other. In the first case we would do a bilateral contrast, while in the second we would do a unilateral one.

It is usually considered more correct to perform a bilateral contrast. However, if we have information that allows us to affirm which may be greater, the contrast may be one-sided. The latter is less conservative, which means that it is easier to reach statistical significance, although this should not be the reason for choosing it.

The confidence level

The usual is to choose a confidence level of 95%, with which we will get a point estimate for the difference of means with its confidence interval of 95%. Thus, we will obtain the value of the standard normal distribution that leaves out, on each side, 0.025 (2.5%) of the population. This value is what is known as Zα, where α is the significance level (the complement of the confidence level).

For example, if we choose a confidence level of 95%, α will be equal to 0.05 and will correspond to a Z of 1.96 for a bilateral contrast. We can calculate this with a statistical program or use one of the many tables available on the Internet and in statistics books.

The power of the study

The power of the study is the probability that the difference can be detected, if it actually exists in the population.

The most common is to select a power of 80% (β = 0.2) or 90% (β = 0.1). Starting from this value, and in a similar way to what we did with α, we will calculate the value of Zβ that we will use, as we will see later, to calculate the sample size.

As we will see in a moment, the values of Zα and Zβ are added and squared to calculate a K value, which is the one we use with the sample size formula.

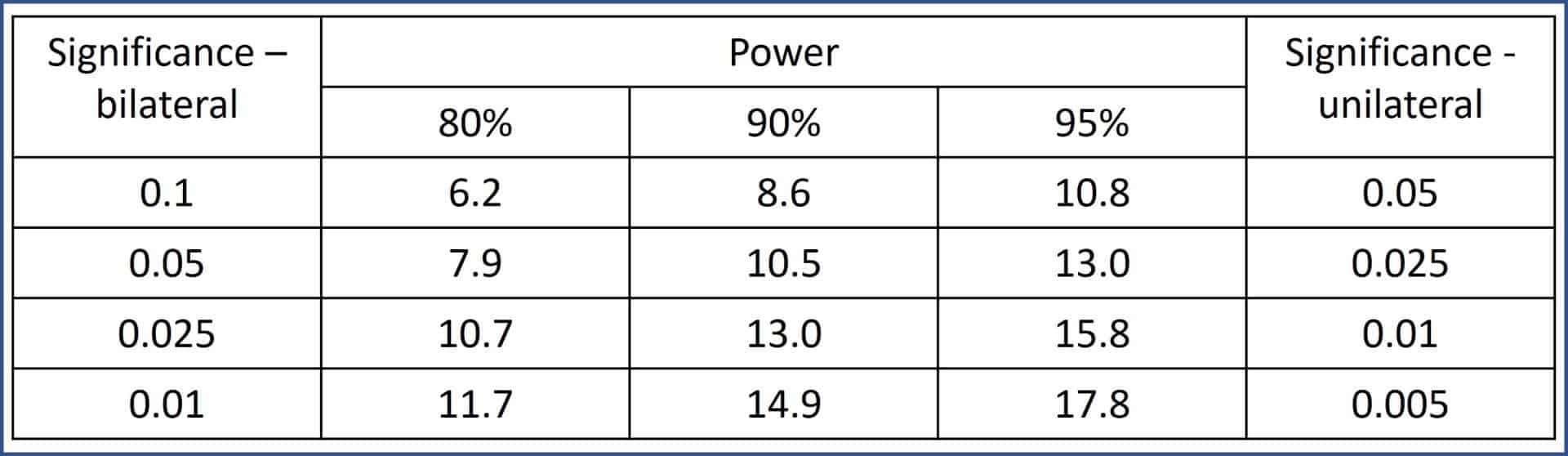
In the attached table you can see the most frequently used K values based on the level of significance, power and type of contrast.

The precision of the study

We have already said it, we want to know what difference between the two means we want to be able to detect.

Naturally, we would like to carry out more precise studies, but this has a cost in the necessary sample size, so we will have to find a midpoint of balance.

The variance in the two groups

This is a value that we must know or estimate in order to calculate the sample size.

Logically, the greater the dispersion of the variable in the population, the more difficult it will be to calculate the sample size for the same level of confidence and precision, which will translate into a larger necessary sample size.

Sample size for the comparison of two means

I think it is time to know the formula that will allow us to calculate the sample size necessary to compare two means. You can see it below.

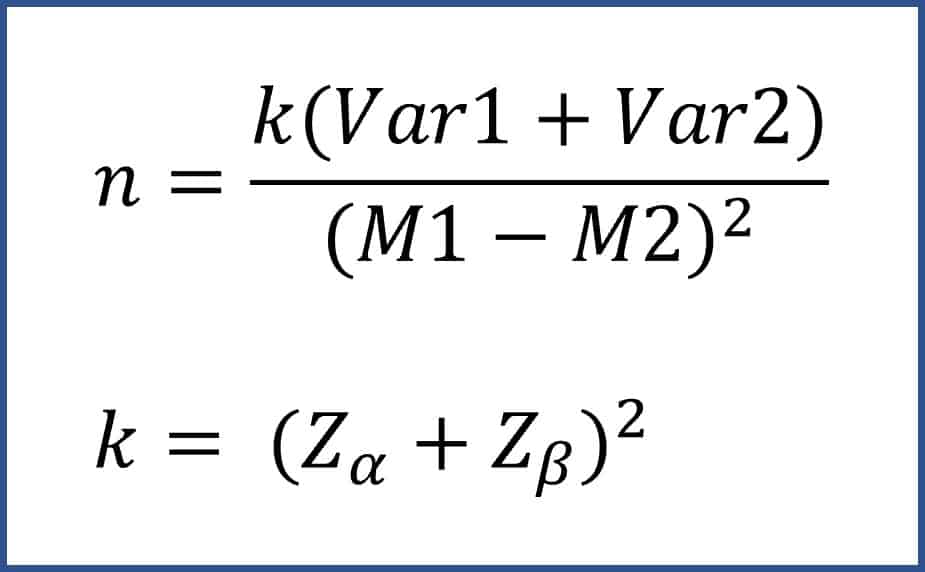
As you can see, the sample size increases proportionally to the square of α and β. This means that K (and, therefore, the sample size) will be greater the lower the level of confidence or the higher the power of the study. The same can be said with the variance of the study, also in the numerator. In this case we can add the two variances or, if preferred, previously calculate the common variance.

Furthermore, the required sample increases inversely proportional to the square of the precision. This means that the smaller the difference we want to detect (greater precision), the larger the sample needed. Furthermore, as it varies with the square of the detectable difference, small decreases in it will lead to large increases in sample size.

Let’s look at an example

Let’s continue with our example of serum cholesterol.

Suppose we have a completely fictitious study that tells us that the standard deviation of cholesterol is the same in boys and girls, 35 mg/dl.

Now we want to know how many participants we need to compare the means in the two genders with a confidence level of 95%, a power of 80% and a two-sided contrast. Lastly, we want to be able to detect a difference of 10 mg/dl in mean cholesterol values.

If we substitute in the formula, K = 7.9, Var1 = Var2 = 35² and the mean difference to be detected is 10 mg/dl. If we solve the equation we will see that we need 193 participants in each group to make the estimate we want.

You can see it in the attached application. I encourage you to vary the different options so that you can see how they influence the necessary sample size.

We are leaving…

And with this we end today.

Although calculating the sample size for the comparison of two means is quite simple, I advise you not to do it by hand and use one of the calculators available on the Internet. We have seen how to compare the two means when the variable is quantitative. Of course, we can also calculate the sample needed to compare two proportions when we are working with a categorical variable. But that is another story…