Mann-Whitney’s U test

Definitely, two different ways of seeing the world and not just a choice that every student has to make when the time comes.

Those most interested in explaining physical and natural phenomena will undoubtedly choose science. For their part, those who are most interested in trying to understand their peers, the so-called human beings, will be candidates for arts.

And do not think that this is a question only of our times. It was already raised in the first universities of the thirteenth century, where one could choose between trivium (grammar, dialectics and rhetoric) and quadrivium (arithmetic, geometry, astronomy and music). You see, the seven liberal arts divided into the two categories: sciences and arts.

And all this comes to my mind because of a problem that my brother-in-law, who is a teacher, posed to me the other day. It turns out that he wants to know if his students are more prepared to choose science or arts next academic year.

To have something to fall back on, he has taken math test scores from a sample of the class and History test scores from another sample of other students in the class, and he wants to analyze what the students are better qualified for. My brother-in-law’s problem is that he’s an arts’ guy, so he has no idea how to do it and he hasn’t thought of anything else but to ask me, a sciences’ guy.

Let’s see how we can solve the problem.

Statement of the problem

The notes of my brother-in-law’s students in the two exams are the ones you see below:

– Mathematics (M): 5, 7, 9, 3, 10, 6, 7, 8, 7 and 2.

– History (H): 6, 8, 7, 9, 5, 10, 10, 5, 4 and 8.

What do you think? Are they better at sciences or arts?

Seeing the 20 qualifications it is difficult to answer the question. It seems that the marks are quite uniform in the two exams.

If we calculate the average, we will see that it is 6.4 for maths and 7.2 for History. Almost a point higher for the story scores, so we would lean towards arts.

In any case, we are beginning to doubt whether the mean is the most appropriate centralization measure for this problem. We see that there are extreme values (10s and some 2s) that can bias the value of the mean, especially in this small sample. So we compute the medians, which are 7 for math and 7.5 for History.

We see that a small difference remains in favor of the History grades, but, of course, it is a very small sample and the difference is not very big, so this difference could be due to chance and, in fact, the students could have similar performance in both subjects.

We need to perform a hypotheses contrast to know the probability of obtaining a difference like the one observed due to chance.

Mann-Whitney’s U test

We have already seen in a previous post that the choice of statistical contrast test depends, among other factors, on the type of variables that we want to contrast.

In our example, we want to compare the means (quantitative variable) for the two categories of a qualitative variable (asignature, with two categories: M and H). The test of first choice is the Student’s t test for the comparison of two independent means.

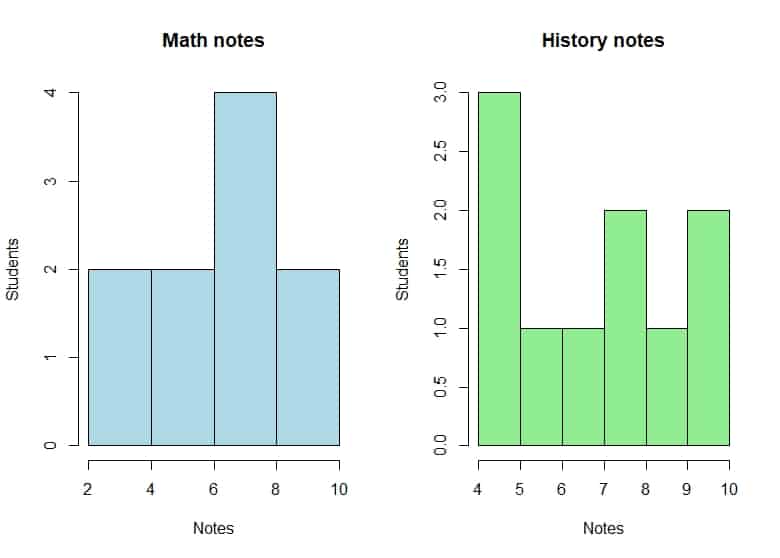
However, in order to make a Student’s t test, the quantitative variable must be distributed normally for the two categories of the qualitative variable, which we doubt will be true in our case.

There are several ways to check for normality. In this case, the simplest is to draw the histograms of the marks of the two subjects, which you can see in the attached figure.

Seeing the graphs we no longer need to do more tests. It seems clear that the variables are not normally distributed. In case we had any doubts with such a small sample, it is clear that we cannot do a Student’s t test. What can we do? We can use its nonparametric alternative, which is the Mann-Whitney’s U test, also called the Wilcoxon’s rank-sum test.

Rationale for the Mann-Whitney’s U test

As a non-parametric test that it is, the Mann-Whitney’s U test requires ordering the ranks of the results of the dependent variable, so it does not compare means, but rather medians.

The great advantage of this test is that it is free from the requirements and assumptions of parametric tests. Its drawback is that it is less powerful than the parametric alternative, so it will cost more to reach our desired p < 0.05.

The systematics to perform the contrast requires the following steps:

1. Sort the ranks of the continuous variable results for the two categories combined.

2. Add the ranks of the two categories separately.

3. Compare the two sums to decide if the difference is due to chance.

Let’s see these three steps.

Sort the ranks

If we order the scores of the two exams, we will obtain the following list:

– M: 2, 3, 5, 6, 7, 7, 7, 8, 9 and 10.

– H: 4, 5, 5, 6, 7, 8, 8, 9, 10 and 10.

Next, we group the grade ranks for the two subjects into a single ordered list, as you can see in the table below.

Once combined, we are going to order the ranks from 1 to 20, with 1 being the lowest grade and 20 being the highest one, as you can see in the next table:

The problem is that there is more than one student who gets the same grade. For example, there are 3 students who get a 5, one in Mathematics and two in History, in the fourth to sixth positions. In order to not to discriminate against any of them and give them the same order number (the same rank), we are going to calculate the average rank of the three and say that the three students are in fifth position.

We do the same with all the notes, as you can see in the table, finally obtaining the list of ordered combined ranks, as shown in the bottom row of the table.

Add the ranks

The Mann-Whitney’s U test assumes the null hypothesis that the medians of the two groups are equal. In the event that the p value is less than 0.05, we will reject the null hypothesis and assume that the medians are different.

How does this relate to the ordered rank lists we’ve built? If we think about it a bit, if the two groups are similar, they will have a similar number of elements in the first position, in the second, and so on. In this way, if we add the ranks of each group, the value of the sum must be similar if the null hypothesis of equality of medians is fulfilled.

Let’s add the ranks in our example:

– M: 1 + 2 + 5 + 7.5 + 10.5 + 10.5 + 10.5 + 14 + 16.5 + 19 = 96.5.

– H: 3 + 5 + 5 + 7.5 + 10.5 + 14 + 14 + 16.5 + 19 + 19 = 113.5.

We see that the sum of ranks is greater in the History test. Since the highest ranks are those of the highest scores, this means that the grades are better in History than in Mathematics. My brother-in-law’s students are more gifted for arts.

Are we sure?

Compare rank sums

We can’t be sure just by looking at the difference between 113.5 and 96.5. We have to calculate the probability that, if they are equal, chance explains this difference.

Internally, the Mann-Whitney’s U test, with formulas that are so unpleasant that we won’t put them here, calculates a U statistic and, from that U value, a z value (which follows a normal distribution) with which the value of p can already be calculated.

An alternative is to look for a table of critical values ​​of the difference of the sums of ranks, which you can find on the Internet or in Statistics books. I show you an example in the last table:

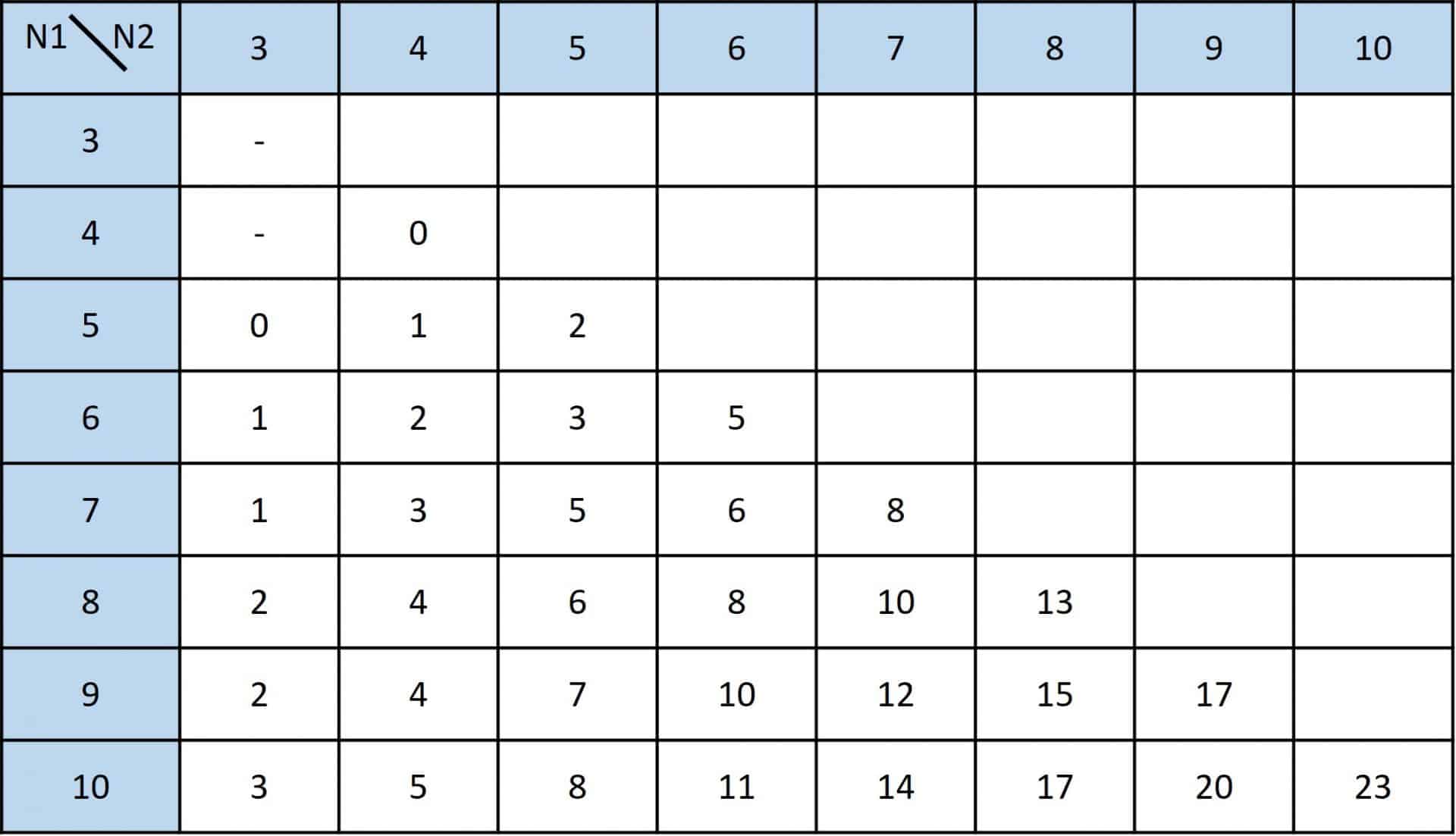
In this table you can see the critical values ​​for two samples (n1 and n2) with a bilateral contrast and a significance level of 0.05.

In our case, this value is 23. This means that any difference of less than 23 points will be explained by chance with a probability greater than 0.05. Of course, if the difference is greater than 23, the probability that it is by chance will be so low that we will believe it. In other words, it will be statistically significant.

The difference that we have observed is 113.5 – 96.5 = 17. As our difference does not reach the critical value of 23, we can conclude that the difference found is not statistically significant. We do not know the exact value of p, but it is sure to be above 0.05, so we cannot reject the null hypothesis of equality of medians.

A simpler way to do the same calculation

All this that we have seen so far is very instructive to understand how the Mann-Whitney’s U test works, but no one thinks to do all these calculations manually, as I have shown you.

We are going to see how we can facilitate the whole process using a statistical program, such as the R program. We would do it in the following steps:

1. We introduce the scores of the two subjects, Mathematics (M) and History (H):

noteM <- c(5, 7, 9, 3, 10, 6, 7, 8, 7, 2)

noteH <- c(6, 8, 7, 9, 5, 10, 10, 5, 4, 8)

2. We combine all the notes successively into a single vector:

notes <- c(noteM, noteH)

3. We create the labels for each subject:

subject <- c(rep("M",10), rep("H", 10))

4. We obtain the vector of ordered ranks from smallest to largest:

ranks <- rank(notes)

5. We calculate the sums of the ranges for each subject:

tapply(ranks, subject, sum)

R gives us the same values ​​again, 113.5 for History and 96.5 for math. We would only have to subtract both and see in the table if the difference exceeds the critical value.

The recommended way to do it

To finish this post, we are going to see the recommended way to solve this problem. Even if a statistical program is used, it is not recommended to do this by hand. It is recommended to use the function that the program will already have to perform the Mann-Whitney’s U test.

In addition to simplicity, we will thus obtain the exact value of p and we will not have to resort to any table to decide whether to accept or reject the null hypothesis.

Once the data has been entered, as we saw previously (notaM and notaH), we would only have to write:

wilcox.test(noteM, noteH)

R will give us a value of the W statistic of 41.5, which corresponds to a value of p = 0.54.

As the value of p is greater than 0.05, we cannot reject the null hypothesis, so we will have to assume that the small difference between the grades of the two subjects is due to chance. My brother-in-law can rest satisfied, he has prepared his students well so that they can choose what they like best.

We are leaving…

And here we end for today.

We have seen how we can compare two means when the assumptions necessary to perform a parametric test are not met. Well, in reality we would no longer be comparing two means, but rather the ranks of the values for the two categories of the qualitative variable.

Seeing how it is done manually, it is also clear why the Mann-Whitney’s U test is also called the Wilcoxon’s rank-sum test (not to be confused with the Wilcoxon’s signed rank test). And why these two names? Well, because there are two methods of making this contrast, although here we have only seen one of them.

And what would happen if we want to add to the comparison the marks of one or more other asignatures? In this case, we would have to resort to the non-parametric alternative of the analysis of variance, which is none other than the Kruskal-Wallis’ test. But that is another story…