Métodos analíticos de normalidad.
El índice de simetría y el índice de apuntamiento, también llamado curtosis, son dos de los cuatro primeros momentos de una distribución normal. Ambos pueden utilizarse para comprobar el supuesto de normalidad de una distribución de datos, aunque son menos utilizados que los métodos de contraste o los gráficos.
La distribución normal no deja de sorprendernos por su belleza y armonía, a la vez que por su sencillez.
Una distribución tan en el centro de la inferencia estadística es muy fácil de caracterizar, solo necesitamos saber su media y su varianza (o la raíz cuadrada de esta última, la desviación estándar o típica).
Pero eso no quiere decir que todas las series de datos que sigan una distribución normal son iguales si las representamos gráficamente. Todas tienen una forma acampanada similar, son más o menos igual de estilizadas y, también, más o menos simétricas.
¿Y por qué digo “más o menos”? Pues porque, en la vida real, nada ni nadie es perfecto, ni siquiera la distribución normal. Bueno, la distribución normal estándar sí que cumple las características de una distribución normal perfecta.
Una distribución normal estándar se caracteriza por tener una media igual a cero y una varianza igual a uno. Suele representarse como N(0,1). Pero, además, podemos caracterizarla a partir de sus momentos.
Un momento… o mejor, cuatro
Algunos os preguntaréis a qué me refiero con lo de los momentos de la distribución. Vamos a verlo.
Los momentos desde el punto de vista estadístico no tienen nada que ver con el tiempo. Más bien, están inspirados en los momentos de la física, que tienen que ver con los centros de masas de los sistemas.
Aquí no tratamos con masas, sino con series de valores que siguen una distribución de probabilidad determinada.
El primer momento lo calculamos como la suma de los valores de la variable dividida por el número total de valores de la distribución. Esto, todos aquellos que estéis todavía despiertos lo habréis entendido, no es otra cosa que la media de la distribución.
Para calcular los demás momentos vamos a utilizar la suma de las diferencias de cada valor de la variable respecto a la media de la distribución. El problema es que, al ser la distribución simétrica, unas diferencias se anularán con otras de forma que el promedio de diferencias sería cero.
La solución al problema de las diferencias que se anulan unas con otras es elevarlas al cuadrado, con lo que las negativas se convierten en positivas. Al dividir esta suma entre la n de la distribución, ¿adivináis lo que obtenemos? En efecto, la varianza, el segundo momento. Aquí tenéis la fórmula para verlo más claro:
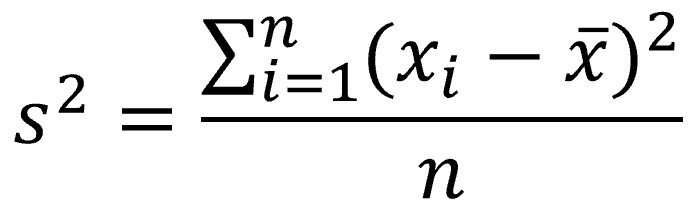
Si continuamos jugando con las diferencias y las elevamos al cubo, ¿qué creéis que pasaría? Pues calcularemos el promedio del cubo de las desviaciones de los valores con respecto a la media, que sería el tercer momento de la distribución.
Si pensamos un poco, en seguida nos daremos cuenta de que al elevar al cubo ya no perdemos los signos negativos.
De esta forma, si hay predominio de valores negativos (la distribución tiene más valores menores que la media) el resultado será negativo y, por el contrario, si predominan los valores mayores que la media, será positivo (la distribución estará sesgada hacia la derecha).
Si dividimos este promedio de suma de diferencias al cubo entre el cubo de la desviación típica, obtendremos la versión adimensional del tercer momento de la distribución, que no es otro que el índice de simetría o sesgo de la distribución.
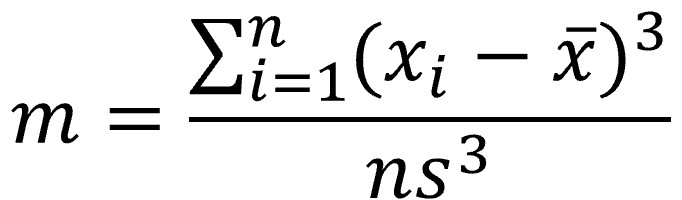
Podéis ver en la primera figura dos ejemplos de distribución, una de ellas simétrica (figura de la izquierda) y la otra sesgada hacia la derecha.
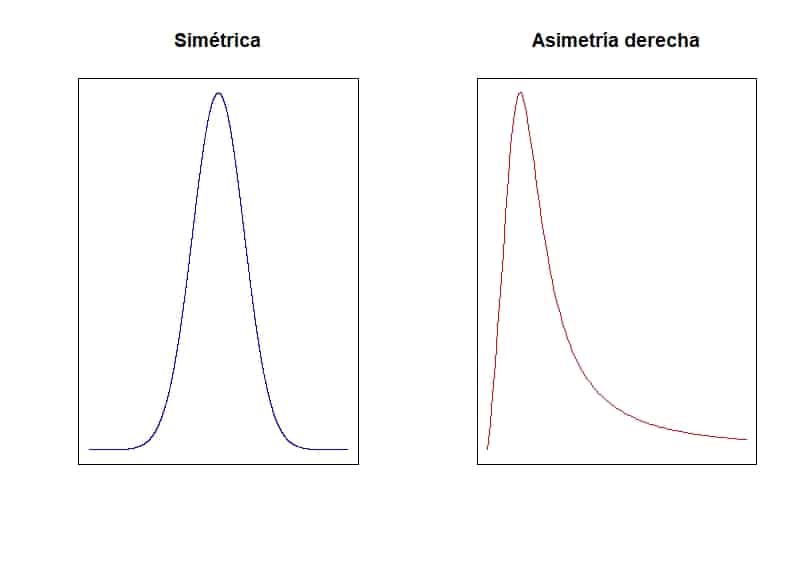
Por último, vayamos un paso más allá y calculemos la suma de las diferencias entre cada valor y la media elevadas a la cuarta potencia y dividida por la n de la distribución. Este sería el cuarto momento, que podemos dividir entre la desviación típica elevada a la cuarta potencia:
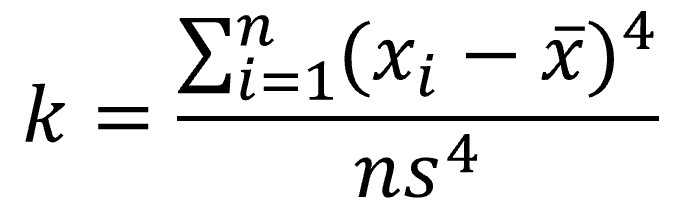
Obtenemos así la versión adimensional del cuarto momento, conocido como índice de apuntamiento o curtosis, que mide cómo de puntiaguda es la campana que forma la representación de la distribución.
En este punto tenemos que hacer una aclaración. La curtosis de la normal estándar es igual a 3. Por este motivo, se suele utilizar la conocida como exceso de curtosis, restando 3 a la fórmula:
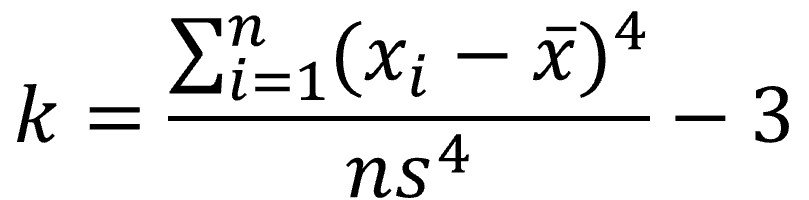
Esto se hace así, explicado de forma muy sencilla, para forzar que el valor de la curtosis de la distribución normal estándar sea 0.
Este índice indica de forma indirecta la cantidad de datos de la distribución cercanos a la media. Así, a mayor grado de curtosis, la distribución será más puntiaguda y las colas serán más ligeras. Y al revés, con curtosis más bajas, habrá menos datos alrededor de la media y las colas serán más pesadas.
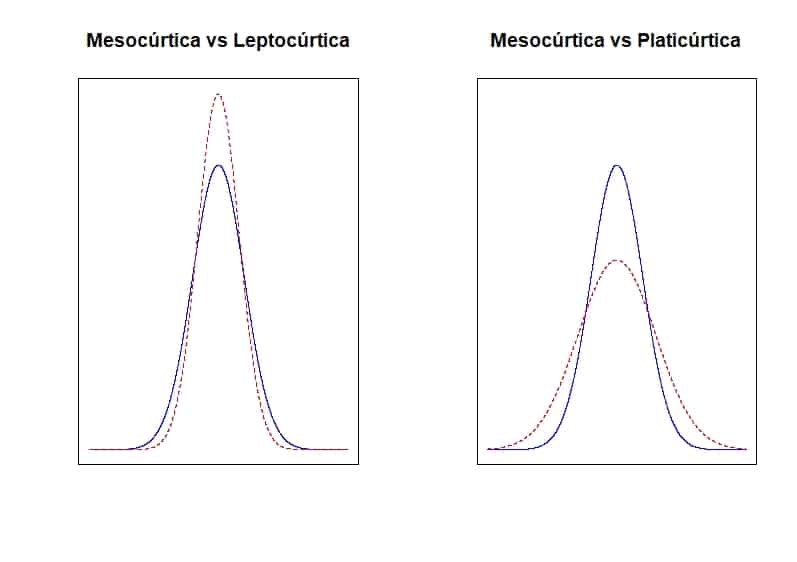
Basándonos en esto, diremos que la distribución es leptocúrtica si es muy puntiaguda (los valores están muy agrupados alrededor de la media). Por el contrario, si los valores están dispersos por los extremos, la llamaremos platicúrtica (será menos puntiaguda) y, si ni una cosa ni la otra, hablaremos de una distribución mesocúrtica.
En la segunda figura que os adjunto podéis comparar una distribución normal mesocúrtica con una leptocúrtica (izquierda) y una platicúrtica (derecha).
Los momentos de la distribución normal estándar
Los valores de los dos primeros momentos ya los hemos mencionado. Una distribución normal estándar es la que tiene media 0 y varianza 1: N(0,1).
Gracias a la perfección de la distribución normal estándar, su índice de simetría vale exactamente 0.
En el caso del índice de apuntamiento o curtosis, para la normal estándar, como buena distribución mesocúrtica, su valor es de 3, aunque ya hemos dicho que hacemos una corrección para llevarlo a 0. Así, las distribuciones son platicúrticas cuando la curtosis es menor de 0 y leptocúrticas cuando es mayor de 0.
Métodos analíticos de normalidad
La utilidad de estos momentos va más allá del puro divertimento matemático y de buscar propiedades de las distribuciones.
Y es que al genial Pearson se le ocurrió que podía comprobarse si una variable seguía una distribución normal calculando los índices de simetría y de apuntamiento y viendo que no se diferenciaban de una forma estadísticamente significativa de los de una normal estándar.
Esto es tan sencillo que podríamos hacerlo incluso de forma manual. Solo tendríamos que calcular los índices de la distribución con las fórmulas que hemos visto y ver si se diferencian de forma estadísticamente significativa mediante una prueba de la t de Student.
Para calcular el estadístico t dividiríamos cada índice por su error estándar y calcularíamos la probabilidad de obtener, por azar, un valor igual o mayor que el que hemos encontrado (sabemos que t sigue una distribución de la t de Student con n-1 grados de libertad).
Sabiendo que el error estándar del índice de simetría es la raíz cuadrada de 6 dividido entre el tamaño de la muestra y el de la curtosis la raíz de 24 entre n, vamos a hacer un ejemplo práctico para entender mejor todo lo que hemos dicho hasta ahora.
Veamos un ejemplo
Vamos a ver un ejemplo práctico utilizando el paquete estadístico R.
Lo primero que necesitamos son las distribuciones de las variables que queremos analizar. Vamos a jugar con ventaja y vamos a generar dos distribuciones, una que ya sabemos que es normal (nm) y otra log-normal (ln). Ejecutamos en R los siguientes comandos:
set.seed(1234)
nm <- rnorm(1000, 0, 1)
ln <- rlnorm(1000, 0, 1)
Las dos distribuciones tienen 1000 elementos, una media de 0 y una desviación típica de 1. El primer comando (set.seed) lo utilizo para que, si seguís el ejemplo, nos genere a todos la misma serie de números aleatorios y vuestras distribuciones sean las mismas que las mías.
Otro preparativo previo que tenemos que hacer es cargar el paquete timeDate de R, para disponer de dos de sus funciones: skewness() y kurtosis(). Lo hacemos con el siguiente comando:
library(timeDate)
Ya podemos empezar. Vamos primero con la distribución que sabemos que es normal. Podemos calcular primero su índice de asimetría con el comando skewness(nm). El programa nos dice que su valor es -0,0051.
Como vemos, muy próximo a 0. Vamos a hacer la prueba de la t de Student. Calculamos el estadístico t dividiendo el índice de asimetría por su error estándar:
t_snm <- skewness(nm)/sqrt(6/1000)
El estadístico t vale -0,067. Para calcular la probabilidad de obtener un valor como este o más alejado del cero, ejecutamos el siguiente comando:
1-pt(-0,067, 999)
El valor de p es de 0,52. Al ser p > 0,05, no podemos rechazar la hipótesis nula de igualdad. En otras palabras, la diferencia con 0 no es estadísticamente significativa.
Ahora calculamos la curtosis con el comando kurtosis(nm). Su valor es de 0,2354, próximo a 0. De todas formas, repetimos el procedimiento de la t de Student:
t_knm <- kurtosis(nm)/sqrt(24/1000)
1-pt(t_knm, 999)
El estadístico t vale 1,52, lo que nos da un valor de p de 0,064. Vuelve a ser mayor de 0,05, luego la diferencia no es significativa. Conclusión: podemos decir que nm sigue una distribución normal.
Veamos ahora que pasa con ln, que sigue, como ya sabemos, una distribución diferente a la normal.
Calculamos primero su índice de simetría con el comando skewess(ln). Nos da un valor de 4,1081. Está alejado de 0 pero, ¿podría explicarlo el azar? Hagamos la t de Student:
t_sln <- skewness(ln)/sqrt(6/1000)
1-pt(t_sln, 999)
t vale 53,03, con una p < 0,05. La diferencia es significativa, por lo que rechazamos la hipótesis nula de que la distribución se ajusta a una normal.
Para terminar, veamos que ocurre lo mismo con la curtosis. Si introducimos el comando kurtosis(ln) nos da un valor de 29,75. Hacemos la t de Student:
t_kln <- kurtosis(ln)/sqrt(24/1000)
1-pt(t_kln, 999)
El valor de t es 192,06, con un valor de p = 0. La distribución no sigue una normal.
Nos vamos…
Y con esto vamos a ir terminando y dejar reposar un poco las neuronas. Espero no haberme ensañado mucho con la matemática, pero es que uno empieza y lo difícil es parar.
Antes de acabar, me gustaría aclarar dos cosas.
La primera, he simplificado mucho la explicación de los momentos. Espero que no venga nadie que de verdad sepa de estas cosas y me lea la cartilla.
La segunda, con toda la belleza matemática, estos métodos analíticos raramente se usan para estudiar el ajuste a la normalidad de una distribución. Lo habitual es usar métodos más sencillos (con ayuda de un programa informático) de tipo de contraste (como la prueba de Shapiro-Wilk o la de Kolmogorov-Smirnov) o métodos gráficos (como el histograma o el gráfico de comparación de cuantiles). Pero esa es otra historia…
