F1-score.

Have you ever felt that a stranger has burst into your world, an intruder who, although seemingly alien, seems destined to be seen with some frequency? Data science, a kingdom in constant expansion, has brought with it a new tool, the F1-score (or F1-measure), unknown to many, at least among those addicted to the world of medicine. Although it may sound like something out of a science fiction movie and seem as mysterious as a UFO, the F1-score has decided to land in the field of medical publications, where it seems to have found an unexpected home.

So, if you’re ready to discover how this interloper from another world can improve the way we evaluate our diagnostic tests, join me on this journey through the surprising intersection between data science and medicine.

Our usual metrics

Although there are multiple tools for evaluating diagnostic tests, the four most loved by the public are the pair formed by sensitivity and specificity, and the two predictive values, positive and negative. Let’s remember what they consist of.

When we want to evaluate a diagnostic test, the usual thing is to compare it with another test that we consider the reference standard, the gold standard. The positives and negatives of the two tests are represented in a contingency table and, using the values in the cells, we make our calculations.

You can see, in the next table, a fictitious example that compares two tests to diagnose that terrible disease that is fildulastrosis. On the one hand, magnetic fildulastrin (MF), our reference standard. On the other hand, a new but very promising test, the green corpuscle cell (GC).

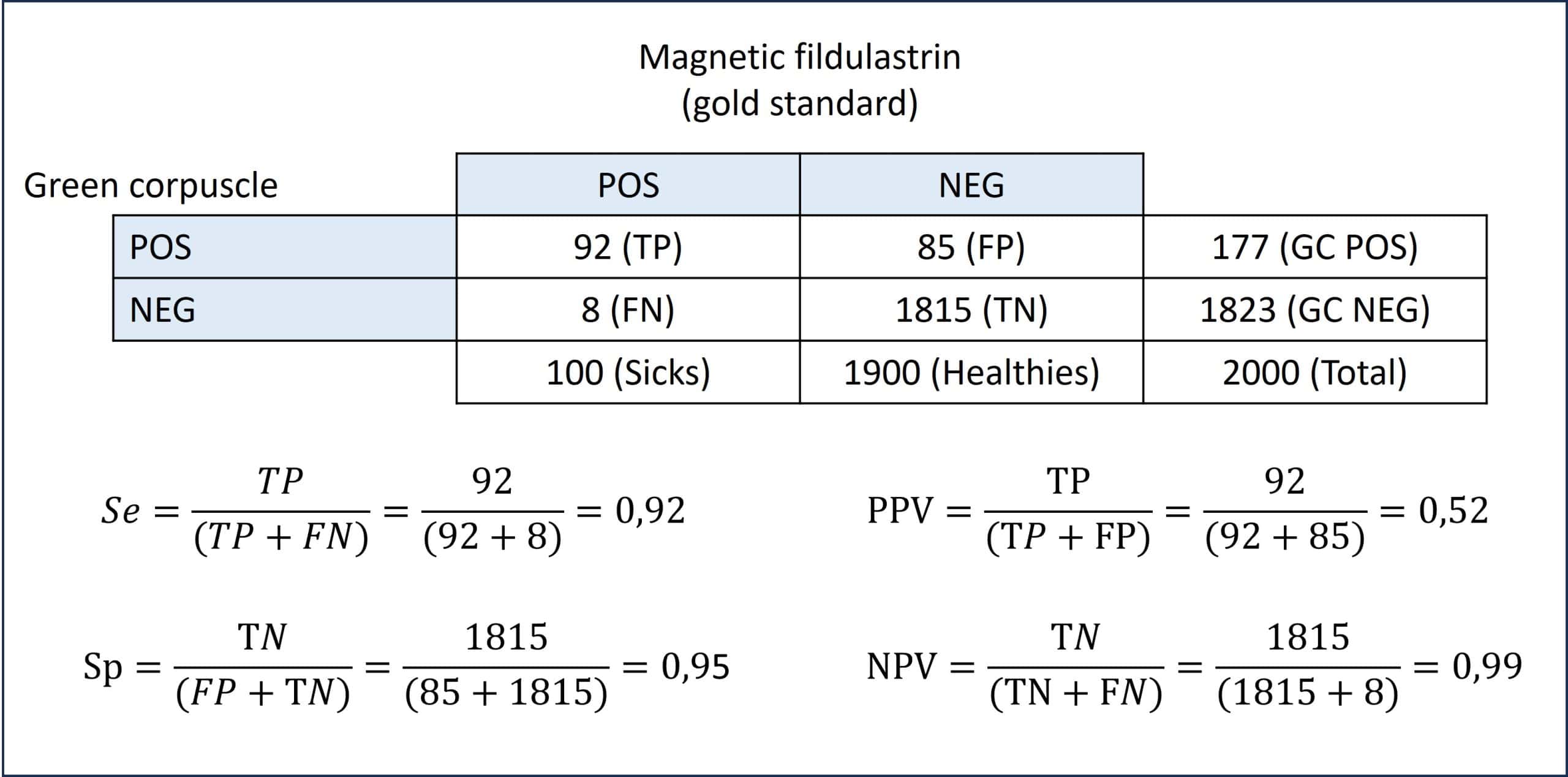
We can see that our sample is made up of 2000 subjects, 100 of whom suffer from fildulastrosis and 1900 healthy.

Of the 100 patients, 92 have a positive GC test. They are the true positives (TP). Furthermore, of the 1900 healthy people, 1815 have negative GC. They are the true negatives (TN).

But we see that the GC test misclassifies some people. Eight of the sick patients test negative (false negatives, FN) and 85 of the healthy patients test positive (false positives, FP). With these four cells we build our indicators to evaluate the test under study (the GC, in our example).

Sensitivity (Se) is the ability to correctly classify sick people. It is the quotient between the TP and the total number of patients (TP + FN). In our example, 0.92.

Specificity (Sp) is the ability to correctly classify healthy people. It is the quotient between the TN and the total number of healthy people (FP + TN). In our example, 0.95.

Let’s go with the predictive values. The positive predictive value (PPV) is the proportion of positives who are sick. It is the quotient between the TP and all the positives (TP + FP). In our example, 0.52. The negative predictive value (NPV) is the proportion of negatives who are healthy. It is the quotient between TN and all negatives (TN + FN). In our example, 0.99.

To complete our analysis of the table, let’s calculate the prevalence of disease. We know that it is the total number of sick patients divided by the total number of participants. In our example, 0.05 (or 5%, whichever we like best).

The problem of lack of balance

Given the example table and the calculations we have done, do you think that the GC test is a powerful diagnostic test?

Those of you who are more diligent will tell me that this is difficult to answer without knowing the likelihood ratios of the test and, without a doubt, you will be right. Let’s calculate them.

The positive likelihood ratio (PLR) tells us how much more likely it is to have a positive result in a sick person than in a healthy person. We know that the probability of testing positive in a sick person is Se and that the probability of testing positive in a healthy person will be that of misclassifying that healthy person, that is, the complementary of Sp. If we calculate Se / (1 – Sp) = 18.4.

The negative likelihood ratio (NLR) tells us how much more likely it is to find a negative result in a sick person than in a healthy person. The probability of finding a negative in a sick person will be that of not classifying him correctly, that is, the complementary of Se. The probability that a healthy person will test negative is Sp. If we calculate (1 – Se) / Sp = 0.08.

A PLR > 10 indicates that the test is very powerful for diagnosis when it gives a positive result. Similarly, a NLR < 0.1 also tells us that the test is very powerful in ruling out the disease when it is negative. However, we see that, although Se and Sp have very good values, the PPV is quite poor (0.52). What is this about?

Indeed, the culprit for this low predictive value is the prevalence of the disease, which is low. For the same value of Se and Sp (or likelihood ratios), the PPV decreases as the prevalence of the disease is lower. In our example, furthermore, this difficulty in correctly classifying patients is aggravated by the great difference between the proportions of sick and healthy people. Think that if, instead of doing the diagnostic test, we always say that the person is healthy, we will be right 95% of the time. The test does not have a simple task, but it is a matter of chance and Bayes’ theorem.

Diagnostic haggling

At this point, if we want to assess the usefulness of the test to help us determine whether or not a specific patient has the disease, we will have to fundamentally calibrate its Se and PPV.

The Se tells us the probability that a patient will have a positive result, but once we already know that he is sick. Seen another way, it gives us an idea of the patients that we will be able to diagnose with the test. If the Se is very high, there will be few patients on whom we test who will remain without a positive diagnosis.

The PPV does not say a very different thing: the probability that a positive person is sick. If the PPV is low, there will be healthy people who will be diagnosed as sick (FP), more so the lower the PPV.

The problem is that, in many situations, especially when the distributions of test result values between healthy and sick are not well separated, when one of the two improves, the other will worsen, and vice versa. Which one interests us more?

If the disease is very serious, we will be interested in a high Se so that no patient goes undiagnosed. The price that will have to be paid will be a more or less high number of FP.

On the contrary, imagine a disease that is not so serious and whose treatment is expensive or annoying. We will prefer not to have FP, even if we miss some undiagnosed patients. In this case, we will be interested in having a better PPV, even if the Se is lower.

In any case, it would be good for us to have a single parameter that summarizes the overall behavior of the test in terms of Se and PPV, especially if we are trying to choose which one may be most useful among different options.

This is where our otherworldly intruder comes to our aid.

An intruder comes to our aid: F1-score

The F1-score, also called F-score or F-measure, is an estimator of the classification capacity of a test that is frequently used in data science and artificial intelligence algorithms and that, recently, has been opening up step between medical articles.

The F1-score is the harmonic mean of the Se and the VPP, so we can define it according to the following formula:

F1 = 2 / (Se ^-1 + PPV ^-1 )

This formula is usually transformed into its friendlier version, which is the following:

F1 = 2 x Se x PPV / (Se + PPV)

The possible values of the F1-score range between 0 and 1. A perfect test (a perfect classifier, as we would say in data science) has an F1-score = 1 (both its Se and its PPV will be worth 1). At the other extreme, the minimum possible value is 0, which will occur when Se and/or VPP are 0.

In this way, the F1-score gives a global idea of the performance of the test based on its Se and its PPV. In our example, the F1-score = 0.65, which would indicate that the test has a moderate capacity to discriminate healthy and sick (what its likelihood ratios already have announced yet).

Let’s imagine that the result of our green corpuscle test is a continuous value and that we have to define the cut-off point to distinguish between positives and negatives. In this case, we can increase the Se by lowering the cut-off point, but we will have many false positives (the PPV will be lower). On the contrary, if we increase the cut-off point we will improve the PPV of the test, but we will probably begin to miss undiagnosed patients (the Se will drop).

We can use the value of the F1-score as we evaluate the different cut-off points. For example, if we are interested in increasing the PPV, we can increase the cut-off point until the moment when the value of the F1-score begins to decrease noticeably. This will mean that, probably, we will have sacrificed the Se of the test excessively in our efforts to improve its PPV , so the number of patients left undiagnosed may be higher than what is convenient for us (yes, but the number of false positives will be lower).

One thing we must keep in mind is that the F1-score, since it depends directly on the PPV, shares with it the defect of depending on the prevalence of the disease. Logically, the same diagnostic test performed in two different populations will show a higher F1-score value in the population in which the prevalence of the disease is higher.

For this reason, if we want to compare tests between different populations, it may be better to use other estimators that do not affect prevalence (as much), such as the likelihood ratios or the area under the ROC curves.

The intruder has a family

Until now we have talked about F1- score but it would be more correct to talk about the F-score (without the 1) when we refer to the estimator in a general way.

We have already seen that F-score represents a balance between Se and PPV. The most common situation is a balanced balance between the two parameters, but there may be times when we are interested in giving priority to one over the other.

Thus, we find a whole family of Fβ measurements , β being the parameter that allows us to choose the balance between Se and PPV that interests us most.

Thus, we can understand the Fβ-score as an abstraction of the F-score in which the calculation of the harmonic mean of Se and VPP is controlled by this parameter β. We can see how the equation for the calculation would look:

Fβ = ((1 + β² ) x Se x PPV) / ( β² x (Se + PPV))

The neutral value in this balance is the one that corresponds to β = 1. In that case, the previous equation remains as the unmodified harmonic mean and we obtain the F measure that balances Se and VPP.

Although, in theory, we could choose the value of β that we wanted, in practice only three of them are usually used:

              – β = 0.5. It gives more importance to the PPV than to the Se, so it will help us to minimize the number of false positives. We will use it to establish the cut-off point when it harms more to have false positives than false negatives (that we miss undiagnosed patients).

              – β = 1. It is the F1-score that we have talked about before. It balances Se and PPV (or false positives and negatives) in a similar way.

              – β = 2. This value decreases the weight of the PPV and increases that of the Se. That is, it is preferred to minimize false negatives (undiagnosed patients) even if false positives increase.

As you can see, it is a continuous haggling. When it comes to diagnostic tests, as in life, you can’t always have everything and you have to choose what you prefer to prioritize.

We’re leaving…

And with this we are going to finish this post.

You see that the realm of diagnostic tests is wide and that there is room for many different estimators to assess the performance capacity of the tests.

This is because no test is perfect in everything, so most of the time we will have to choose whether to favor false positives, false negatives or whatever interests us most.

We have mentioned, although only in passing, that this problem can increase when there is a great imbalance between the proportion of sick and healthy people (very low disease prevalence). In these cases, the task of the diagnostic test becomes complicated and it may be difficult to choose the most appropriate cut-off point for our needs. In addition to the F-score, we have some other measure, also coming from the world of data science, that helps us with the haggling between Se and VPP.

I am referring specifically to the so-called enrichment of precision with respect to recovery (or PPV with respect to Se, in our usual language), closely related to the concepts of pre-test and post-test probability . But that is another story…